Toy cart tied to the end of an unstretched string of length a, when revolved moves in a horizontal circle of radius 2a with a time period T. Now the toy cart is speeded up until it moves in a horizontal circle of radius 3a with a period T. If Hooke's law (F=kx) holds, then
T'=√32T
T'=(√32)T
T'=(32)T
T' = T
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the toy cart under the influence of Hooke's law and centripetal force.
Step 1: Understand the initial conditions
The toy cart is tied to a string of length a and revolves in a horizontal circle of radius 2a with a time period T. The elongation of the string when the cart is at radius 2a is:
x1=2a−a=a
Step 2: Apply centripetal force
The centripetal force required for the cart to move in a circle is provided by the spring force, which follows Hooke's law:
F=kx1=k⋅a
This force must equal the centripetal force, which is given by:
Fc=mv2r=mv22a
Setting these equal gives:
k⋅a=mv22a
Step 3: Relate speed and time period
The speed v can be expressed in terms of the time period T:
v=2π(2a)T=4πaT
Substituting this into the centripetal force equation:
k⋅a=m(4πaT)22a
This simplifies to:
k⋅a=m⋅16π2a2T2
k=8mπ2T2
Step 4: Analyze the new conditions
Now, the toy cart is moved to a radius of 3a with the same time period T. The new elongation x2 is:
x2=3a−a=2a
Step 5: Set up the new centripetal force equation
The new centripetal force must also be equal to the spring force:
F=kx2=k⋅2a
And the centripetal force is:
Fc=mv′2r=mv′23a
Setting these equal gives:
k⋅2a=mv′23a
Step 6: Substitute k from earlier
Substituting k from the previous step:
8mπ2T2⋅2a=mv′23a
This simplifies to:
16mπ2aT2=mv′23a
Cancelling m and rearranging gives:
v′2=48π2a2T2
Step 7: Relate v′ to the new time period T′
The new speed v′ can also be expressed in terms of the new time period T′:
v′=2π(3a)T′
Squaring this gives:
v′2=4π2(3a)2T′2=36π2a2T′2
Step 8: Set the two expressions for v′2 equal
Equating the two expressions for v′2:
48π2a2T2=36π2a2T′2
Cancelling π2a2 gives:
48T2=36T′2
Cross-multiplying gives:
48T′2=36T2
Thus,
T′2=3648T2=34T2
Taking the square root gives:
T′=√32T
Final Result
The new time period T′ is:
T′=√32T
The toy cart is tied to a string of length a and revolves in a horizontal circle of radius 2a with a time period T. The elongation of the string when the cart is at radius 2a is:
x1=2a−a=a
The centripetal force required for the cart to move in a circle is provided by the spring force, which follows Hooke's law:
F=kx1=k⋅a
This force must equal the centripetal force, which is given by:
Fc=mv2r=mv22a
Setting these equal gives:
k⋅a=mv22a
The speed v can be expressed in terms of the time period T:
v=2π(2a)T=4πaT
Substituting this into the centripetal force equation:
k⋅a=m(4πaT)22a
This simplifies to:
k⋅a=m⋅16π2a2T2
k=8mπ2T2
Now, the toy cart is moved to a radius of 3a with the same time period T. The new elongation x2 is:
x2=3a−a=2a
The new centripetal force must also be equal to the spring force:
F=kx2=k⋅2a
And the centripetal force is:
Fc=mv′2r=mv′23a
Setting these equal gives:
k⋅2a=mv′23a
Substituting k from the previous step:
8mπ2T2⋅2a=mv′23a
This simplifies to:
16mπ2aT2=mv′23a
Cancelling m and rearranging gives:
v′2=48π2a2T2
The new speed v′ can also be expressed in terms of the new time period T′:
v′=2π(3a)T′
Squaring this gives:
v′2=4π2(3a)2T′2=36π2a2T′2
Equating the two expressions for v′2:
48π2a2T2=36π2a2T′2
Cancelling π2a2 gives:
48T2=36T′2
Cross-multiplying gives:
48T′2=36T2
Thus,
T′2=3648T2=34T2
Taking the square root gives:
T′=√32T
The new time period T′ is:
T′=√32T
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View Solution
Knowledge Check
A particle of mass M is moving in a horizontal circle fo radius R with unifomr speed V. When it moves from one point to a diameterically opposite point, its
Akinetic energy change by MV2/4Bmomentum does not changeCmomentum changes by 2 MVDkinetic energy changes by MV2
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionUnder the influence of a unifrom magnetic field a charged particle is moving on a circle of radius R with Constnant speed v. The time period of the motion
View SolutionA particle with the constant speed in a circle of radius r and time period T.The centripetal acceleration of a particle is
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average speed of the particle is ……
View SolutionA particle is moving in a circle of radius R with constant speed. The time period of the particle is T. In a time t=T6
Average velocity of the particle is…..
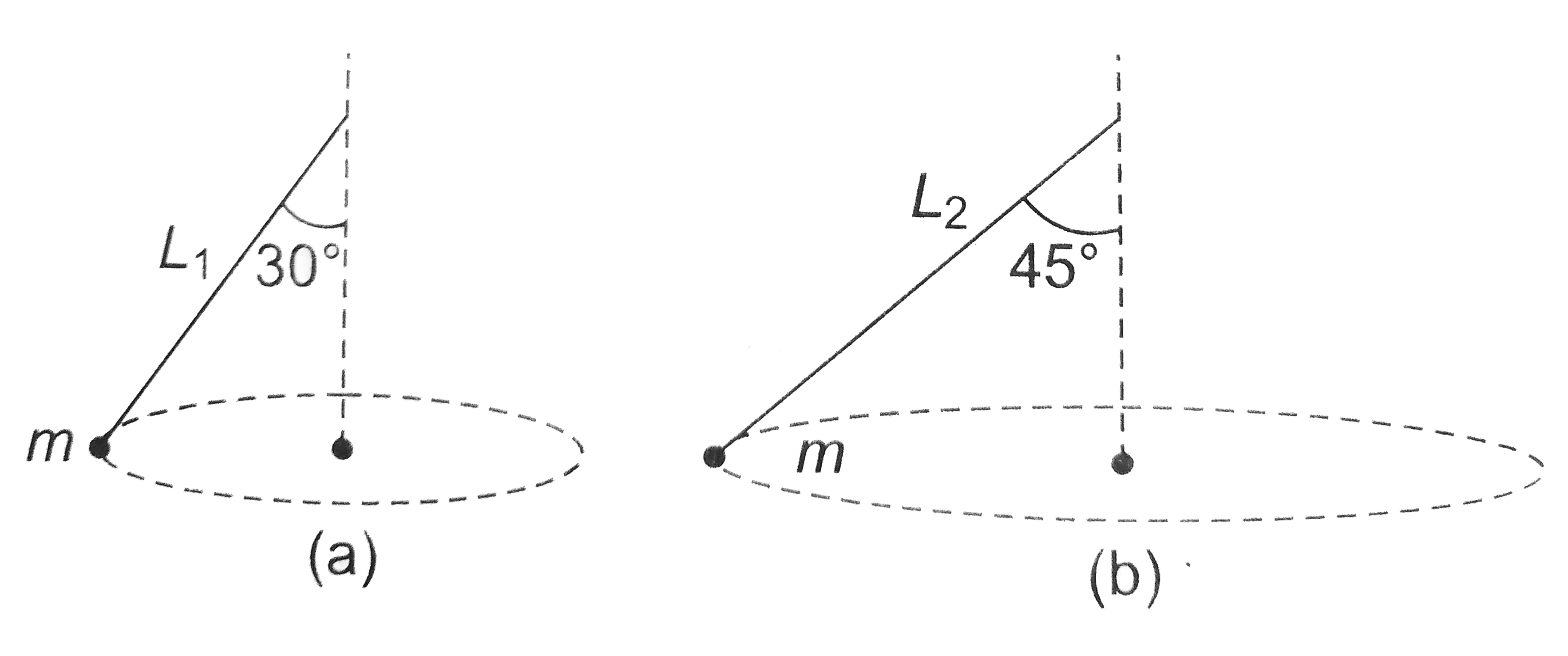
View SolutionTwo partical tied to different strings are whirled in a horizontal circle as shown in figure. The ratio of lengths of the string so that they complete their circular path with equal time period is:
View SolutionA body is moving in a vertical circle of radius r such that the string is just taut at its highest point. The speed of the particle when the string is horizontal is
View Solution
