Illustrative Example from GK PUBLICATIONS PHYSICS (HINGLISH) GRAVITATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| GK PUBLICATIONS PHYSICS (HINGLISH) | Illustrative Example |
| Medium | English |
| Academic Year | 2023-2024 |
Question 4
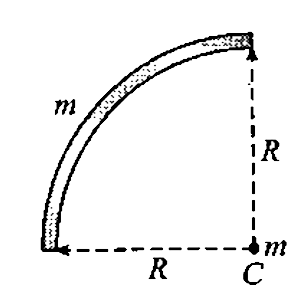
A ring of radius R is made from a thin wire of radius r. If ρ is the density of the material of wire then what will be the gravitational force exerted by the ring on the material particle of mass m placed on the axis of ring of ring at a distance x from its centre. Shown that the force will be maximum when x=R/√2 and the maximum value of force will be given as
Fmax=4π2Gr2ρm(3)3/2R2 View SolutionQuestion 7
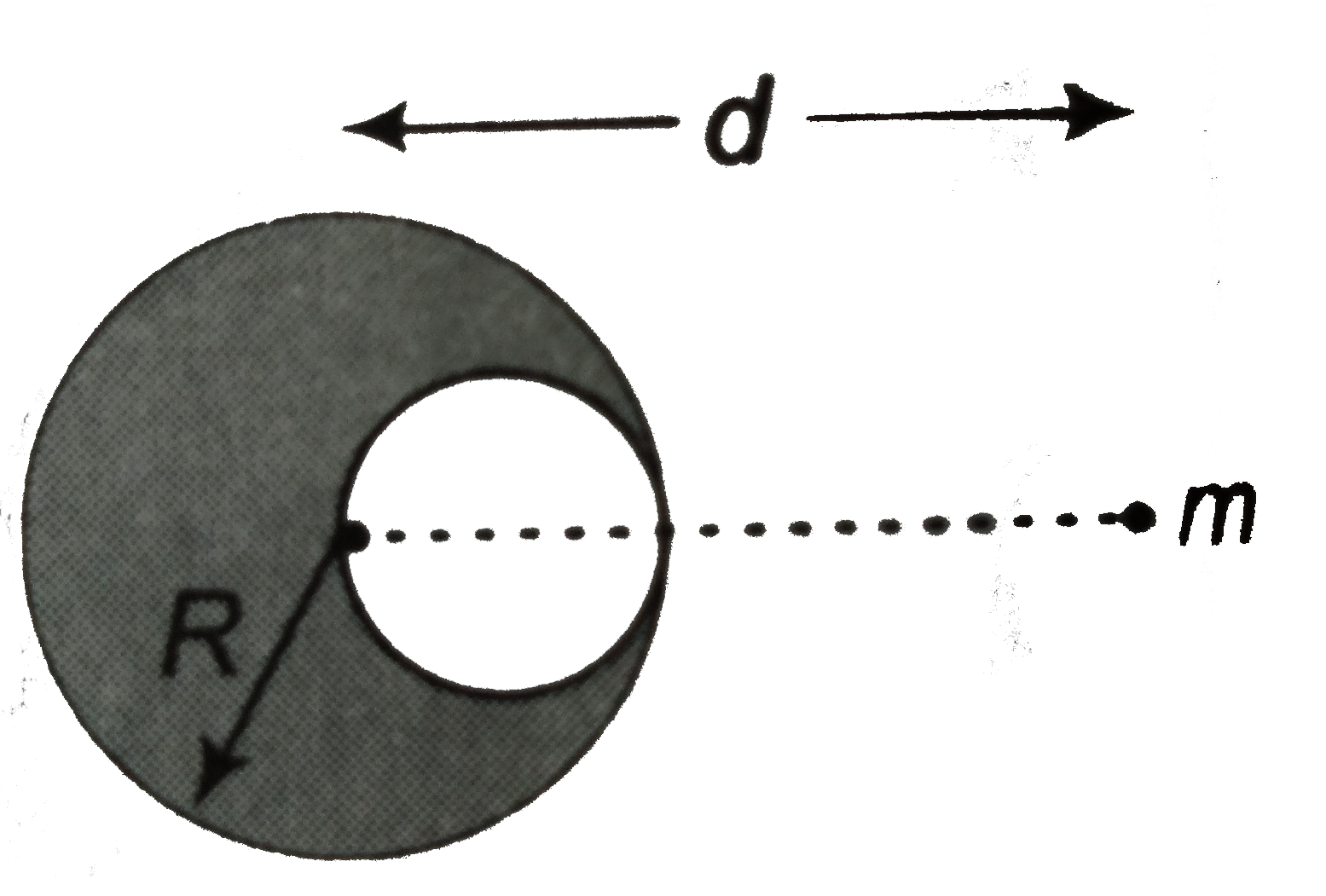
Figure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was M. With what gravitational force does the hollowed out lead sphere attract a particle of mass m that lies at a distance d from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
 View Solution
View SolutionQuestion 9
The small dense stars rotate about their common centre of mass as a binary system, each with a period of 1 year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is r and the distance of the earth from the Sun is R, find the relation between r and R. View SolutionQuestion 15
Three particle each of mass m are placed at the corners of an equilateral at the corners of an equilateral triangle of side d as shown in figure. Calculate (a) the potential energy of the system, (b) work done on this system if the side of the traingle is changed from d to 2d.
 View Solution
View SolutionQuestion 22
Given a thin homogenous disc of radius a and mass m1. A particle of mass m2 is placed at a distance l from the disc on it's axis of symmetry. Initially both are motionless in free space but they ultimately collide because of gravitational attraction. find the relative velocity at the time of collision. assume a<<1.View SolutionQuestion 24
A solid sphere of mass m and radius r initially placed at a distance 5r from the centre of a point mass M as shown in figure. Now During displacement, it is also uniformly expanded to a radius 2 r so that its density decreases uniformly throughout its volume. Find the work required in this process.
 View Solution
View SolutionQuestion 29
An artificial satellite of the earth is to be established in the equatorial plane of the earth and to an observer at the equator it is required that the satellite will move eastward, completing one round trip per day. The distance of the satellite from the centre of the earth will be - ( The mass of the earth is 6.00×1024 kg and its angular velocity = 7.30×10−5rad/sec.) View SolutionQuestion 31
An artificial satellite is describing an eqatorial orbit at 1600 km above the surface of the earth. Calculate its orbital speed and the period of revolution. If the satellite is travelling in the same direction as the rotateion of the earth (i.e., from west to east), calculate the interval between two successive times at which it will appear vertically overhead to an observer at a fixed point on the equator. Radius of earth = 6400km.View SolutionQuestion 33
A satellite ils launched into a circular orbit 1600km above the surface of the earth. Find the period of revolution if the radius of the earth is R=6400km and the acceleration due to gravity is 9.8ms−2. At what height from the ground should it be launched so that it may appear stationary over a point on the earth's equator?View SolutionQuestion 37
Imagine a light planet revolving around a very massive star in a circular orbit of radius r with a period of revolution T. On what power of r will the square of time period will depend if the gravitational force of attraction between the planet and the star is proportional to r−5/2.View SolutionQuestion 38
A meteorite approaching a planet of mass M (in the straight line passing through the centre of the planet) collides with an automatic space station orbiting the planet in a circular trajectory of radius R. The mass of the station is ten times as large as the mass of the meteorite. As a result of the collision, the meteorite sticks in the station which goes over to a new orbit with the minimum distance R/2 from the planet. Speed of the meteorite just before it collides with the planet is : .View SolutionQuestion 40
A satellite is revolving round the earth in a circular orbit of radius r and velocity υ0. A particle is projected from the satellite in forward direction with relative velocity υ=(√5/4−1)υ0. Calculate its minimum and maximum distances from earth's centre during subsequent motion of the particle.View SolutionQuestion 41
A sky lab of mass 2×103kg is first launched from the surface of earth in a circular orbit of radius 2R and then it is shifted from this circular orbit to another circular orbit of radius 3R. Calculate the energy required
(a) to place the lab in the first orbit,
(b) to shift the lab from first orbit to the second orbit. (R=6400km, g=10m/s2) View SolutionQuestion 44
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.View SolutionQuestion 48
A satellite of mass MS is orbitting the earth in a circular orbit of radius RS. It starts losing energy slowly at a constant rate C due to friction if Me and Re denote the mass and radius of the earth respectively show that the satellite falls on the earth in a limit time t given by t=GMSMe2C(1Re−1RS)View SolutionQuestion 49
An artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.View SolutionQuestion 50
An artificial satellite (mass m) of a planet (mass M) revolves in a circular orbit whose radius is n times the radius R of the planet in the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the force of resistance on satellite to depend on velocity as F=av2 where 'a' is a constant caculate how long the satellite will stay in the space before it falls on to the planet's surface. View SolutionQuestion 53
a.Find the radius of the circular orbit of a satellite moving with an angular speed equal to the angular speed of earth\'s rotation. b). If the satellite is directly above the north pole at some instant find the time it takes to come over the equatorial plane. Mass of the earth =6×1024kgView Solution