Particle Exercise from GK PUBLICATIONS PHYSICS (HINGLISH) GRAVITATION for Class 11
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| GK PUBLICATIONS PHYSICS (HINGLISH) | Particle Exercise |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
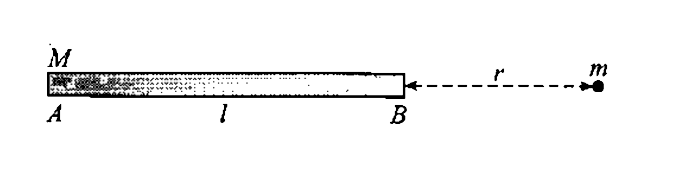
In a double star, two stars (one of mass m and the other of mass 2m) distance d apart rotate about their common centre of mass., Deduce an expressioin for the period of revolution. Show that te ratio of their angular momenta about the centre of mass is the same as the ratio of their kinetic energies.View SolutionQuestion 8
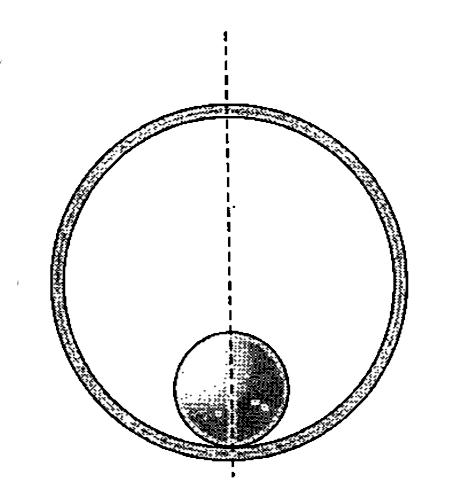
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
 View Solution
View SolutionQuestion 12
A small point mass m is to be thrown with such a speed at a distance x from the axis of a long cylinder of radius R and density ρ, so that m starts revolving around the cylinder in a circular orbit of radius x with centre on the axis of cylinder. Find the speed with which point mass is thrown.View SolutionQuestion 14
What will be acceleration due to gravity on the surface of the moon if its radius were (1/4)th the radius of earth and its mass (1/80)th the mass of earth? What will be the escape velocity on the surface of moon if it is 11.2km/s on the surface of the earth? (given that g=9.8m/s2)View SolutionQuestion 18
A tunnel is dug along a chord of the earth. a perpendicular distance R2 from the earth\'s centre is dropped. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.View SolutionQuestion 24
Distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii a and 2a, respectively. A body of mass m is fired straight form the surface of the larger star towards the smaller star. What should be its minimum inital speed to reach the surface of the smaller star? Obtain the expression in terms of G,M and a.View SolutionQuestion 30
As satellite of mass 1000 kg is supposed to orbit the earth at a height of 2000 km above the earth\'s surface. Find a). its speed in the orbit b). its kinetic energy. c). The potential energy of the earth satelilte system and d). its time period. Mass of the earth =6×1024kg. View SolutionQuestion 32
Assume the radius of the earth to be 6.4×106m
a. Calculate the time period T of a satellite on equational orbit at 1.4×10em above the surface of the earth.
b. What is the speed of the satellite in this orbit?
c. If the satellite is travelling in the same direction as the rotation of the earth i.e. west to east, what is the interval between two successie times at which it will appear vertically overhead to an observed at a fixed point on the equator?View SolutionQuestion 40
A satellite is put in an orbit just above the earth's atmosphere with a velocity √1.5 times the velocity for a circular orbit at the that height. The initial velocity imparted is horizontal. What would be the maximum distance of the satellite from the earth, when it is in the orbit. View SolutionQuestion 42
Two satellites S1 and S2 revolve round a planet in coplaner circular orbit in the same sense. Their period of revolution are 1 hour and 8 hour respectively. The radius of the orbit of S1 is 104km. When S2 is closest to S1, find
(a) The speed of S2 relative to S1,
(b) The angular speed of S2 actually observed by an astronaut is S1 View SolutionQuestion 43
If a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is r1 and maximum distance is r2. Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse. View SolutionQuestion 47
The small dense stars rotate about their common centre of mass as a binary system, each with a period of 1 year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is r and the distance of the earth from the Sun is R, find the relation between r and R. View SolutionQuestion 48
An artificial satellite is moving in a circular orbit around the earth with a speed of equal to half the magnitude of escape velocity from earth.
(i). Determine the height of the satellite above the earth's surface
(ii). If the satellite is stopped suddenly in its orbit and allowed to fall freely on the earth. Find the speed with it hits and surface of earth. Given M="mass of earth & R "="Radius of earth"View SolutionQuestion 49
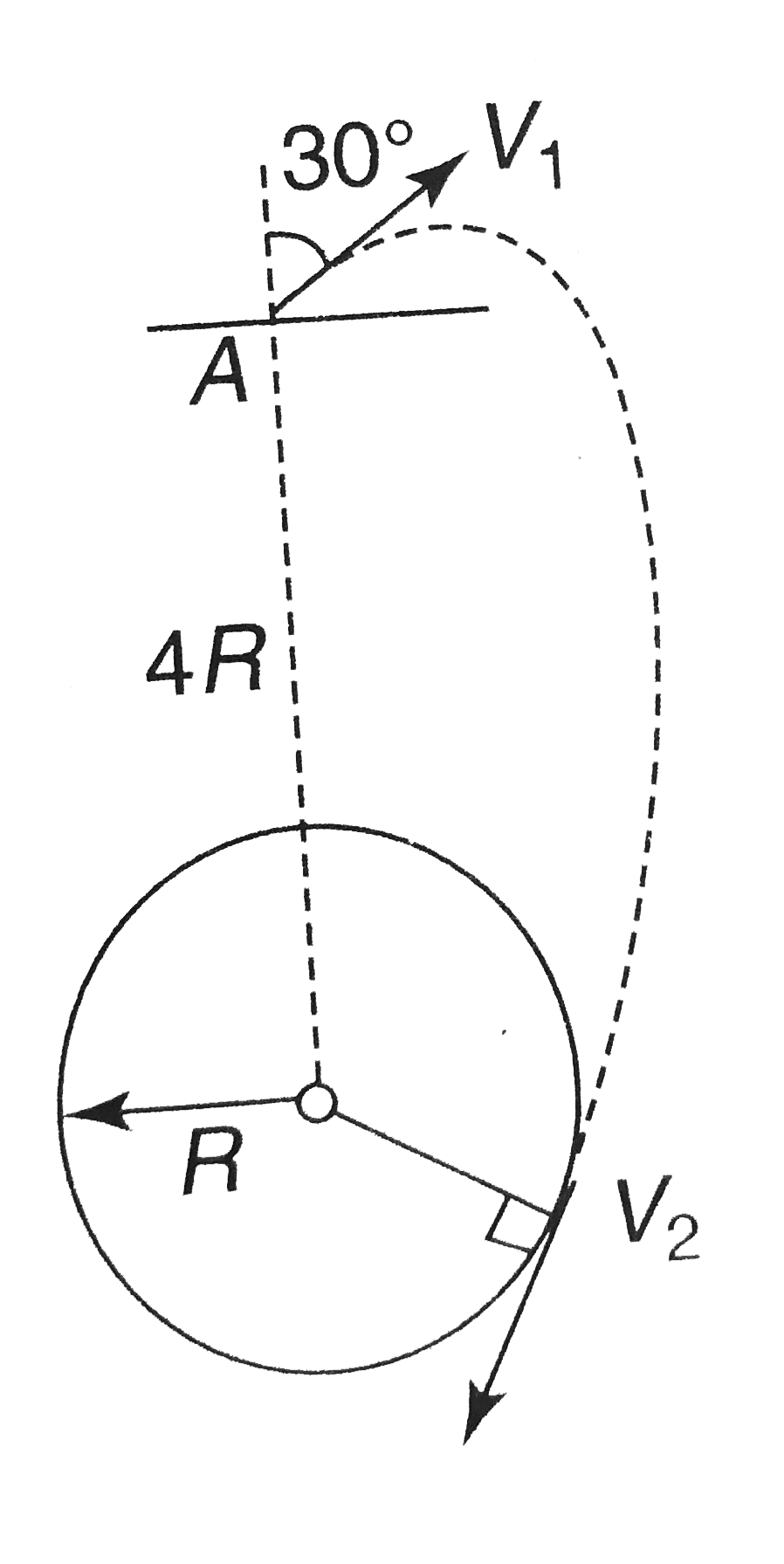
A particle is projected from point A, that is at a distance 4R form the centre of the earth, with speed V1 in a direction making 30∘ with the line joining the centre of the earth and point A, as shown. Consider gravitational interaction only between thesetwo. (Use GMR=6.4×107m2/s2). The speed V1 if particle pasess grazing the surface of the earth is
 View Solution
View SolutionQuestion 52
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the sun and the earth pull these objects in same direction. Is the weight of an object as measured by a spring balance on the earth's surface , more at midnight as compared to its weight as noon?View SolutionQuestion 76
The planet Egabbac (in another solar system) has a radius twice that of the earth's but an average mass density which is the same as the earth. Would the weight of an object on Egabbac's surface to be the same as on the earth's greater than on the earth's or less than on the earth's ? If greater or less than on the earth's then by how much?View SolutionQuestion 96
A particle of mass an charge q is projected vertically upwards .A uniform electric field →E is acted vertically downwards.The most appropriate graph between potential energy U (gravitation plus electrostatic) and height h(<< radius of earth) is :(assume U to be zero on surface of earth)View SolutionQuestion 130
Two identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other isView SolutionQuestion 141
Imagine a light planet revolving around a very massive star in a circular orbit of radius r with a period of revolution T. On what power of r will the square of time period will depend if the gravitational force of attraction between the planet and the star is proportional to r−5/2.View SolutionQuestion 143
Two satellites S1 and S2 revolve around a planet in coplanar circular orbits in the same sense their periods of revolution are 1 hour and 8hours respectively the radius of the orbit of S1 is 104 km when S1 is closest to S2 the angular speed of S2 as observed by an astronaut in S1 is :View SolutionQuestion 146
A body is imparted a velocity v from the surface of the earth. If v0 is orbital velocity and ve be the escape velocity then for :
v=v0 the body follows a circular track around the earth.
(B). v>v0 but <ve, the body follows elliptical path around the earth.
(C). v<v0, the body follows elliptical path and return to surface of earth.
(D). v>ve, the body follows hyperbolic path and escape the gravitational pull of the earth.View SolutionQuestion 165
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
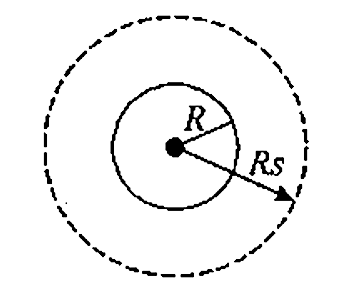
Mass (in kg) of the massive object at the centre of the milky galaxy is of the order :View SolutionQuestion 166
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
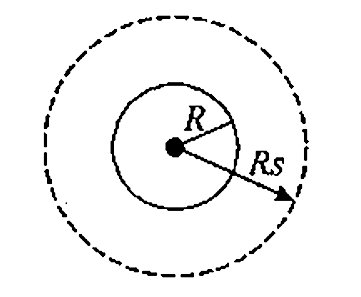
Theories suggest that it is not possible for a single star to have a mass of more than 50 masses. The massive object at the centre of milky way galaxy is most likely to be a :View SolutionQuestion 167
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
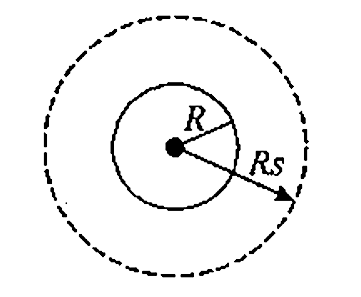
If mass of earth ME≈6×1024kg and its radius RE=6400km, to what fraction of its presents radius does the earth need to be compressed in order to become a black hole ?
(Give only the order of your answer)View SolutionQuestion 175
A satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √ρpra respectively. The angular momentum of the satellite is :View SolutionQuestion 179
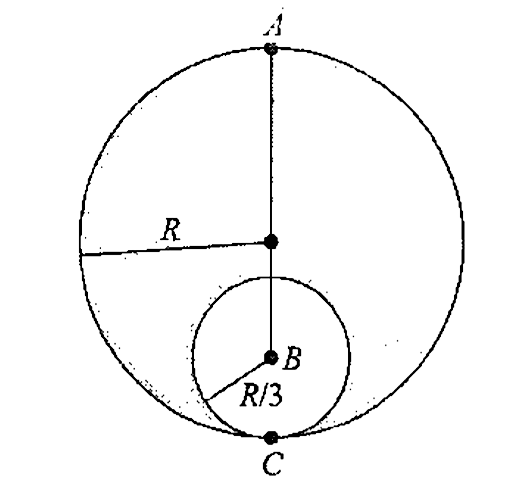
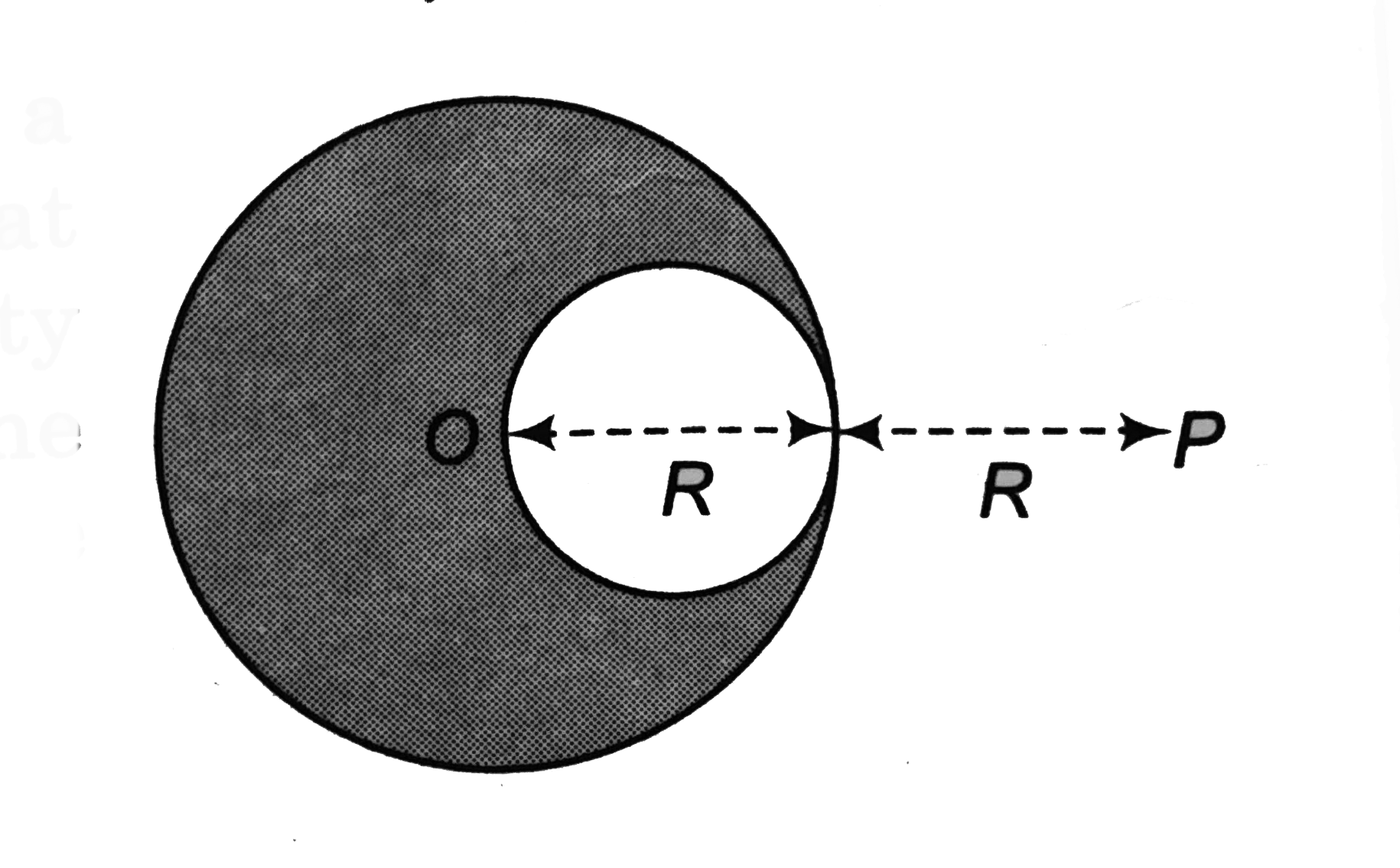
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 View Solution
View SolutionQuestion 190
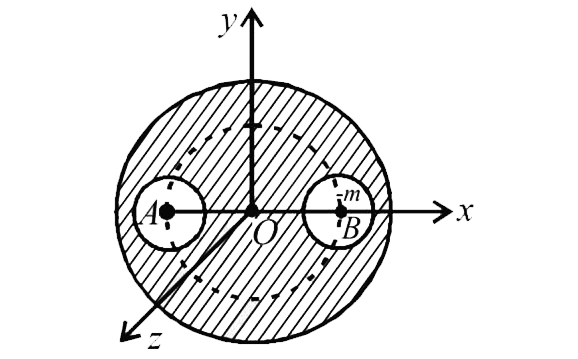
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
 View Solution
View SolutionQuestion 191
Two tunnels - T1 and T2 are dug across the earth as shown in figure. One end of the two tunnels have a common meeting point on the surface of the earth. Two particles P1 and P2 are oscillating from one end to the other end of the tunnels. At some instant particles are at mid point of their tunnels as shown in figure. Then -

(a) Write phase difference between the particle P1 and P2. Can the two particles ever meet?
(b) Write the ratio of maximum velocity of particle P1 and P2. View SolutionQuestion 199
Suppose we invent a unit of mass which we shall call the caendish (C). One cavendish of mass is defined such that G=1.0000(AU)3/(yr2C). Our unit of length is the astronomical unit (AU), the earth-sun distance−1AU=1.496×1011m- and our unit of time is the year (yr). (a) Datermine the conversion factor between C and kg. (b) Find the mass of the sun in C.View SolutionQuestion 202
While investigating the planet Norc in another solar system, we find that the radius of Norc is 9.54×106m and that the period of a satellite put in circular orbit of radius 1.476×107m is 8.09×103s. Determine (a) the mass of Norc, (b) The average, mass density of Norc, (c) the value of the gravitational field on the surface of Norc. (d) If the period of Norc's rotation about its axis is 1.04×104s, what will be the reading on a spring scale (calibrated on earth) supporting a 1.0kg object at Norc's equator ?View SolutionQuestion 204
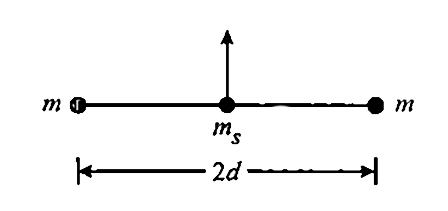
Two point masses, each equal to M, are placed a distance 2a apart. Show that a small mass m placed midway between them on the line joining them will be in equilibrium and if it is slightly displaced from this position along the line perpendicular to the line joining the masses, it will execute simple harmonic oscillations. Calculate the frequnency of these oscillations.View SolutionQuestion 207
Imagine a planet whose diameter and mass are both one half of those of earth. The day's temperature of this planet surface reaches upto 800K. ? Make calculation and tell whether oxygen molecules are possible in the atmosohere of the planet.
[Escape velocity from earth's surface =11.2km/s,k=1.38×10−23J/K, mass of oxygen molecule =5.3×10−26kg].View SolutionQuestion 208
A thin rod of mass M and length L is bent in a semicircle as shown in figure (a). What is its gravitational force (both magnitude and direction) on a particle with mass m at O the centre of curvature ? (b) what would be the force on m if the rod is in the form of complete circle?View SolutionQuestion 209
Three identical particles each of mass "m" are arranged at the corners of an equiliteral triangle of side "L". If they are to be in equilibrium, the speed with which they must revolve under the influence of one another's gravity in a circular orbit circumscribing the triangle is View SolutionQuestion 210
A smooth tunnel is dug along the radius of earth that ends at centre. A ball is released from the surface of earth along tunnel. Coefficient of restitution for collision between soil at centre and ball is 0.5. Calculate the distance travelled by ball just before second collision at centre. Given mass of the earth is M and radius of the earth is R.View SolutionQuestion 211
A particle of mass m is subjected to an attractive central force of magnitude k/r2, k being a constant. If at the instant when the particle is at an extreme position in its closed orbit, at a distance a from the centre of force, its speed is √k/2ma, if the distance of other extreme position is b. Find a/b. View SolutionQuestion 214
A short , straight and frictinless tunnel is bored through the centre of the earth and a body is realesed from the surface into the tunnel . Show that the motion of the body in the tunnell will be simple harmoic and hence calculate the taken by the body to travel from one end of the tunnel to the other (Radius of the earth = 6.38×106m and acceleration due to gravity at the surface = 9.81ms2 View SolutionQuestion 215
An iron ball o fradius 1 m and density 8000kgm−3 is placed in water . A bubble of radius 1 cm at a distance 1.5 m from the centre of the ball . Will there be a force of attraction or repulsion between them and what will be the magnitude of this force ? (Neglect the mass of air and take G=6.67×10−11.)View SolutionQuestion 216
Two satellites A and B of equal mass move in the equatorial plane of the earth, close to earth's surface. Satellite A moves in the same direction as the of the rotation of the earth while satellite B moves in the opposite direction. Calclate the ratio of the kinetic energy of B of that of A in the reference frame fixed to the earth (g=9.8ms−2 and radius of the earth =6.37×106km)View SolutionQuestion 219
A spacecraft is in a circular orbitof radius 3R around the moon as shown in figure-6.109. At point A, the spacraft fires a probe which is supposed to arrive at the surface of the moon at point B. Datermine the necessary velocity vr of the probe relative to the spacecraft just fter ejection. Also calculate the angular displacement θ of the spacecraft when the probe arrives at point B. Assume velocity of spacecraft remains unchanged due to ejection of probe.
 View Solution
View SolutionQuestion 222
What will be acceleration due to gravity on the surface of the moon if its radius were (1/4)th the radius of earth and its mass (1/80)th the mass of earth? What will be the escape velocity on the surface of moon if it is 11.2km/s on the surface of the earth? (given that g=9.8m/s2)View SolutionQuestion 225
A system consists of a thin ring of radius R and a very long uniform wire oriented along axis of the ring with one of its ends coinciding with the centre of the ring. If mass of ring be M and mass of wire be λ per unit length, calculate interaction force between the ring and the wire.View SolutionQuestion 228
If the time period of a satellite TS is different from that of earth's rotation TE and the satellite is moving in the direction of earth's rotation, show that the time interval between two successive appearances of the satellite overhead is given by ltbRgt 1T=1TS~1TE
What will happen to this interval if TS=TEView SolutionQuestion 234
A man of mass m starts falling towards a planet of mass M and radius R. As he reaches near to the surface realizes that he will pass through a small hole in the planet. As he enters the hole he seen that the planet really made of two places a spherical shell of negligible thickness of mass 2M3 and a point mass M3 of centre. Change in the force of gravity experienced by the man isView SolutionQuestion 235
A pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other m. Their centres are a distance d apart, d being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies. View SolutionQuestion 237
The optimal way of transferring a space vehicle from an inner circular orbit to an outer coplanar circular orbit is to fire its engines as it passes through A to increase its speed and place it in an elliptic transfer orbit. Another increase in speed as it passes through B will place it in the desired circular orbit. For a vehicle in a circular orbit about the earth at an altitude h1=320km, which is to be transferred to a circular orbit at an altitude h2=800km, determine :
(a) The required increases in speed at A and B.
(b) The total energy per unit mass required to execute the
 View Solution
View SolutionQuestion 238
A lunar probe is rocketed from earth directly toward the moon in such a way that it always between the earth and the moon. The probe narrowly misses the moon and continues to travel beyond it on an extension of the line segement described above. At what distance from the center of the earth will the force due to the earth be equal to the force due to the moon?View SolutionQuestion 240
A rocket starts vertically upward with speed v0. Show that its speed v at height h is given by v20−v2=2hg1+hR
where R is the radius of the earth and g is acceleration due to gravity at earth's suface. Deduce an expression for maximum height reachhed by a rocket fired with speed 0.9 times the escape velocity.View SolutionQuestion 241
A satellite is in a circular orbit very close to the surface of a planet. At some point it is given an impulse along its direction of motion, causing its velocity to increase n times . It now goes into an elliptical orbit. The maximum possible value of n for this to occur isView SolutionQuestion 245
A projectile is fired vertically upwards from the surface of the earth with a velocity Kve, where ve is the escape velocity and K<1.If R is the radius of the earth, the maximum height to which it will rise measured from the centre of the earth will be (neglect air resistance)View SolutionQuestion 247
A satellite of mass 5M orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass M and the other of masses 4M. After the explosion the mass M ends up travelling in the same circular orbit, but in the opposite direction. After explosion the mass 4M is View SolutionQuestion 250
Consider two satellites A and B of equal mass, moving in the same circular orbit of radius r around the earth but in the opposite sense and therefore a collision occurs.
(a) Find the total mechanical energy EA+EB of the two satellite-plus-earth system before collision.
(b) If the collision is completely inelastic, find the total mechanical energy immediately after collision. Describe the subsequent motion of the combined satellite.View SolutionQuestion 259
Two satellite S1 and S2 revolve around a planet in coplanar circular orbits in the opposite sense. The periods of revolutions are T and ηT respectively. Find the angular speed of S2 as observed by an astronouts in S1, are observed by an astronaut in S1, when they are closest to each other. View SolutionQuestion 264
A cord of length 64m is used to connected a 100kg astronaut to spaceship whose mass is much larger than that of the astronuat. Estimate the value of the tension in the cord. Assume that the spaceship is orbiting near earth surface. Assume that the spaceship and the astronaut fall on a straight line from the earth centre. the radius of the earth is 6400km. View SolutionQuestion 271
Distance between the centres of two stars is 10α. The masses of these stars are M and 16M and their radii a and 2a, respectively. A body of mass m is fired straight form the surface of the larger star towards the smaller star. What should be its minimum inital speed to reach the surface of the smaller star? Obtain the expression in terms of G,M and a.View SolutionQuestion 274
A sapceship nears the Moon along a parabolic trajectory that almost toches the Moon's surface. In order to transfer closest approach. The engine ejects gas ata speed of u=4km/s realtive to the spaceship In its direction of motion. If v1= velocity of spaceship in parabolic trajectory, when it almost touches the earth and v2= velocity of spaceship in circular orbit when it almost to'uches the earth. Then what friction of total mass should the fuel burn to transfer space ship to circular orbit?View SolutionQuestion 277
A Body moving radially away from a planet of mas M, when at distance r from planet, explodes in such a way that two of its many fragments move in mutually prependicular circular orbits around the planet what will be
(i). Then velocity in circular orbits?
(ii). Maximum distance between the two fragments before collision and
(iii). Magnitude of their relative velocity just before they collide?View SolutionQuestion 280
A ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.View SolutionQuestion 283
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.View SolutionQuestion 287
A meteorite approaching a planet of mass M (in the straight line passing through the centre of the planet) collides with an automatic space station orbiting the planet in a circular trajectory of radius R. The mass of the station is ten times as large as the mass of the meteorite. As a result of the collision, the meteorite sticks in the station which goes over to a new orbit with the minimum distance R/2 from the planet. Speed of the meteorite just before it collides with the planet is : .View SolutionQuestion 289
Two lead spheres of 20cm and 2cm diametre respectively are planet with centres 100cm apart. Calculate the attraction between them, given the radius of the Earth as 6.37×108cm and its mean density as 5.53×103kgm−3. Speciffic gravity of lead =11.5. If the lead spheres are replaced by bress sphere of the same radii, would the force of attraction be the same?View Solution
_S01_003_Q01.png)