SOLVED EXAMPLES from S CHAND PHYSICS (ENGLISH) CIRCULAR MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | CIRCULAR MOTION |
| S CHAND PHYSICS (ENGLISH) | SOLVED EXAMPLES |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
A pilot of mass 70 kg in a jet aircraft moves in a vertical circle while executing the loop-the-loop at a constant speed of 200 m/s. If the radius of the circle is 2.5 km what is the force exerted by the seat on the pilot at (a) the top of the loop and (b) the bottom of the loop.View SolutionQuestion 7
A small toy car moves round a circular track of radius 4 m. The car makes one revolution in 10 s. Calculate (a) the speed of the car, (b) its centripetal acceleration, (c) the centripetal force exerted,by the track if the.mass of the car is 200 g, (d) the safe speed with which the car can move around without toppling, if the distance between the wheels is 4 cm and the height of the centre of gravity of the car from the horizontal is 2 cm.View SolutionQuestion 14
A bend in a level road has a radius of 100 m. What is the maximum speed which a car turning this bend may have without skidding if the coefficient of friction between the road and the tyres in 0.3. If the centripetal force is provided by 'banking' what is the angle of banking?View SolutionQuestion 16
A small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
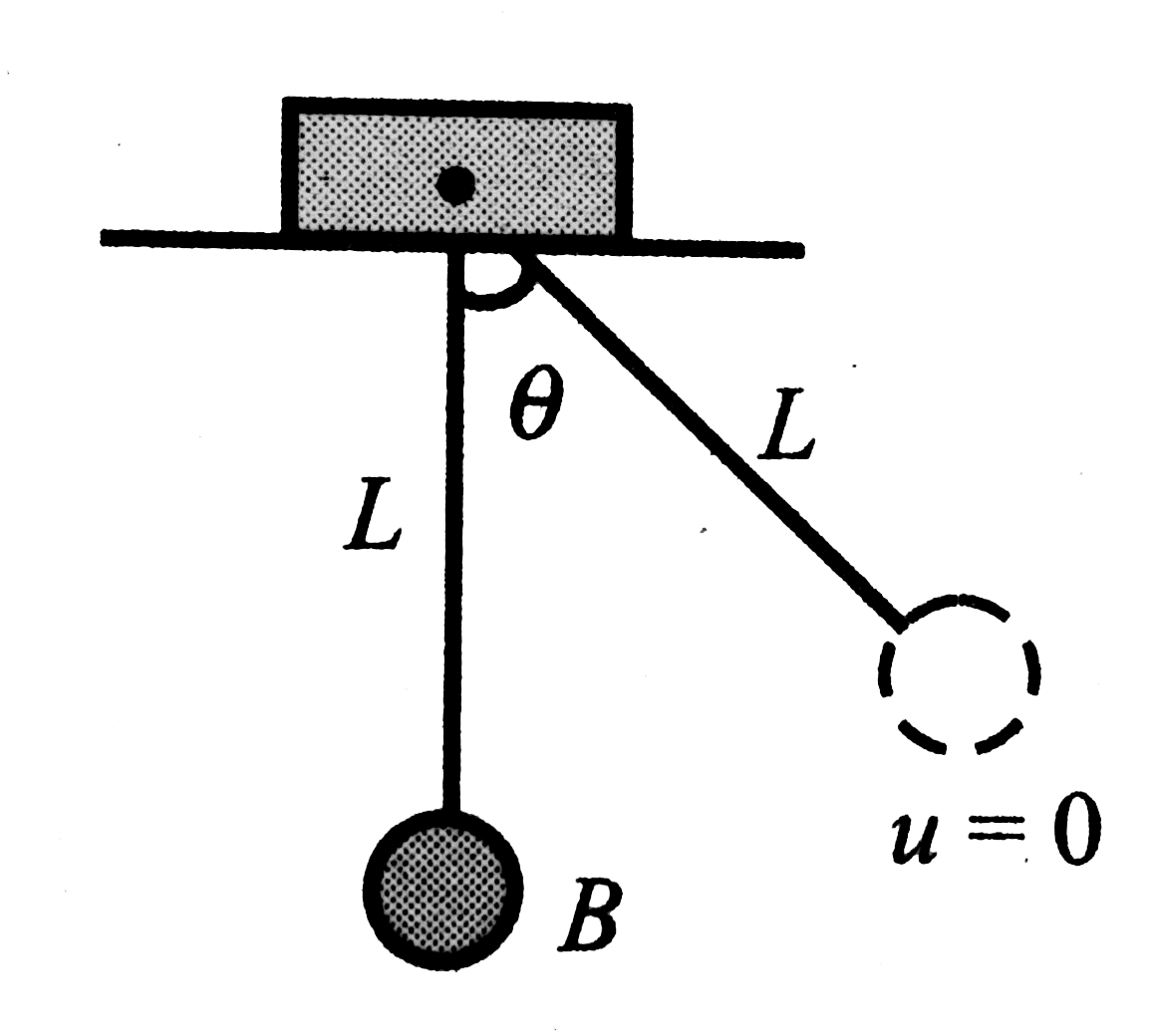 The displacement of centre of mass of A+B system till the string becomes vertical is View Solution
The displacement of centre of mass of A+B system till the string becomes vertical is View SolutionQuestion 17
One end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?View SolutionQuestion 19
A cylclist is riding with a speed of 27kmh−1. As he approaches a circular turn on the road of radius 80m, he applies brakes and reduces his speed at the constant rate of 0.5ms−2. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?View SolutionQuestion 20
A string 1 m long can just support a weight of 16 kg. A mass of 1 kg is attached to one of its ends. The body is revolved in a horizontal circle about the other fixed end of the stringy Find the greatest number of revolutions made by the mass per seconds ? (Take g=10ms−2)
The maximum tension the string can withstand = weight of 16 kg. View SolutionQuestion 24
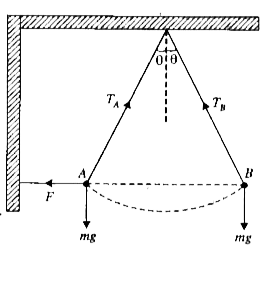
In all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
(A)(##VMCPHYXIWORBOK01_C04E03050_Q01##)Conical pendulum(P)T=mgcosθ(B)(##VMCPHYXIWORBOK01_C04E03050_Q02##)Pendulum is swinging. Angular position is the extreme position.T is tension in extreme position(Q)Tcosθ=mg(C)(##VMCPHYXIWORBOK01_C04E03050_Q03##)The car is moving with constant acceleration.The ball is at rest with respect to car(R)Speed of ball with respect to ground is constant(D)(##VMCPHYXIWORBOK01_C04E03050_Q04##)The car is moving with constant velocity. The ball is at rest with respect to car(S)Velocity of ball with respect to ground is changing continuouslyView SolutionQuestion 25
A sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2). View SolutionQuestion 30
A uniform round object of mass M, radius R and moment of inertia about its centre of mass Icm has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take IcmMR2=k]View SolutionQuestion 34
In the HCl molecule, the separation between the nuclei of two atoms is about 1.27 A (1A=10−10m). Find the approximate location of the CM. of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
 View Solution
View SolutionQuestion 38
The distance between the two atoms in a diatomic molecule O2 is 1.21×10−10 m. The mass of each oxygen atom is 2.66×10−26 kg. Treating the atoms as point masses find the m moment of inertia of the molecule about an axis passing perpendicular to the line joining the centres of the atoms.
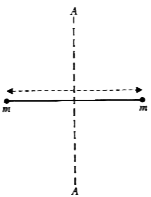 View Solution
View SolutionQuestion 40
A cross-section of a solid cylinder is shown in Fig. 7.2.20, with the core section protruding from the larger drum. A rope wrapped around the drum of radius r1=80 cm exerts a force 10.0 N to the right on the cylinder. The cylinder can rotate freely around the central axis. A rope wrapped around the core of radius r2=40cm exerts a force of 15.0 N downwards on the cylinder, (a) Calculate the net torque acting on the cylinder about the axis of rotation ?
 View Solution
View SolutionQuestion 41
A particle of mass 50 gm moving in a circle at 5 cm radius with a constant speed of 10 cm/s. What is its angular momentum about (i) centre of the circle, (ii) a point on the axis of the circle at 4 cm distance from its centre ? Which of these will be always in the same direction ? [Fig.]
 View Solution
View SolutionQuestion 46
In all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
(A)(##VMCPHYXIWORBOK01_C04E03050_Q01##)Conical pendulum(P)T=mgcosθ(B)(##VMCPHYXIWORBOK01_C04E03050_Q02##)Pendulum is swinging. Angular position is the extreme position.T is tension in extreme position(Q)Tcosθ=mg(C)(##VMCPHYXIWORBOK01_C04E03050_Q03##)The car is moving with constant acceleration.The ball is at rest with respect to car(R)Speed of ball with respect to ground is constant(D)(##VMCPHYXIWORBOK01_C04E03050_Q04##)The car is moving with constant velocity. The ball is at rest with respect to car(S)Velocity of ball with respect to ground is changing continuouslyView SolutionQuestion 48
A point mass 10 g moves in the xy plane with a velocity 2ms−1 along a straight line. Find the magnitude and direction of its angular momentum (i) with respect to the origin O and (ii) with respect to the origin O. The magnitude of the position vector →r is 0.5 m and the angle θ=30∘.
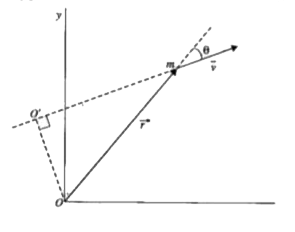 View Solution
View SolutionQuestion 50
A horizontal disc rotating freely about a vertical axis makes 100 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 9 cm from the axis if the number of revolution per minute is thereby reduced to 90. Calculate the moment of inertia of disc.View SolutionQuestion 56
One end of a massless string is wound around a cylinder of mass 5 kg and radius 16' cm. The cylinder' is mounted symmetrically on a horizontal axle so 5 that It can freely rotate about its axis, to the other end of the string a mass of 500 gm is attached. Calculate the acceleration of the mass when it is released from rest.View SolutionQuestion 63
A wheel of mass 1.4 kg and radius 0.4 m is mounted on a frictionless, horizontal axle as shown in Fig. 7.2.50. Alight string wrapped around the rim supports a mass of 2 kg. What is the angular acceleration of the wheel and the tangential acceleration of a point on the rim ? Also find the tension in the string.
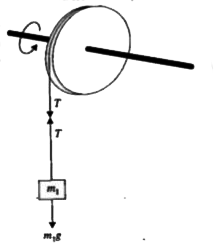 View Solution
View SolutionQuestion 64
In the Atwood's machine shown in Fig. m1=7 kg and m2=12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley of radius 5 cm. When the system is released from rest the heavier mass is found to fall 1 m in 2 s. Calculate the moment of inertia of the pulley ?
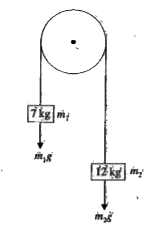 View Solution
View SolutionQuestion 65
The radius of a large hemisphere whose" axis of symmetry is vertical is R = 50 cm. A small sphere of radius r= 5cm rolls without slipping with a speed of 2cm/s. The mass of the sphere is 100 gm. If it start's at the top from rest (i) what is the kinetic energy at the bottom? (ii) What fraction is rotational ? (iii) What fraction is translational?
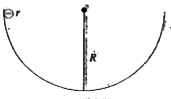 View Solution
View SolutionQuestion 66
The mass of a spool of wire in the form of a uniform solid cylinder is m and its radius is r. The wire is unwound under a constant force F. Assume that the cylinder does not slip, find (i) the acceleration of the centre of mass, (ii) the force of friction, (iii) what is the speed attained by the centre of mass after the cylinder has rolled through a distance, assume that the cylinder starts from rest and it rolls without slipping ?View SolutionQuestion 67
A uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal. View SolutionQuestion 70
A mass m is attached to a string passing through a small hole in a frictionless, horizontal surface. The mass is initially orbiting with a velocity v1 in a circle of radius r1 The string is then slowly pulled from below, decreasing the radius of the circles to r2 (i) What is the speed of the mass when the radius is r2 ? (ii) What is the tension in the string ? (iii) What is the work done in moving the mass m from r1 to r2?
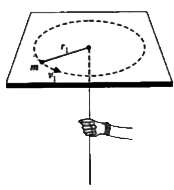 View Solution
View Solution
All Exercises from S CHAND PHYSICS (ENGLISH) Class 11 PHYSICS CIRCULAR MOTION
- MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
- MODULE 1 (FROM ANGULAR VELOCITY)
- MODULE 1 (FROM BANKING OR RAILS AND ROADS)
- MODULE 1 (FROM CENTRIPETAL FORCE)
- MODULE 1 (LONG ANSWER QUESTIONS)
- MODULE 1 (SHORT ANSWER QUESTIONS)
- MODULE 1 (VERY SHORT ANSWER QUESTIONS)
- MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
- MODULE 2 (FROM ANGULAR MOMENTUM - CONSERVATION)
- MODULE 2 (FROM CENTRE OF MASS)
- MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
- MODULE 2 (FROM MOMENT OF INERTIA, TORQUE)
- MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)
- MODULE 2 (LONG ANSWER QUESTIONS)
- MODULE 2 (SHORT ANSWER QUESTIONS)
- MODULE 2 (VERY SHORT ANSWER QUESTIONS)
- SOLVED EXAMPLES