The radius of a large hemisphere whose" axis of symmetry is vertical is R = 50 cm. A small sphere of radius r= 5cm rolls without slipping with a speed of 2cm/s. The mass of the sphere is 100 gm. If it start's at the top from rest (i) what is the kinetic energy at the bottom? (ii) What fraction is rotational ? (iii) What fraction is translational?
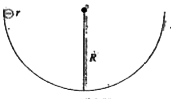
Radius of the small sphere = R=0.5m
Radius of the small sphere =r = 0.05 m
Mass of small sphere m=0.100 kg
Speed = v = 0.02 m/s
Translational kinetic energy =Kr=12mv2
Rotational kinetic energy =Kr=12Iω2
=12×(25mr2)×v2r2=15mv2
Total K.E. of the small sphere =K=Kl+Kr=12mv2+15mv2
K=710mv2=710×0.100×(0.02)2
K=2.8×10−5J
(ii) KrK=(1/5)mv2(7/10)mv2=27
(27) of the total energy is rotational
KtK=(12)mv2(7/10)mv2=57
(57) of the total energy is translational.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
A circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA small steel sphere of mass m and radius r rolls without slipping on the fiictionless surface of a large hemisphere of radius R{R>>r) whose axis of symmetry is vertical. It starts at the top from the rest,
(a) What is the kinetic energy at the bottom ?
(b) What fraction is the rotational kinetic energy of the total kinetic energy ?
(c) What fraction is the rotational kinetic energy of the total kinetic energy?
(d) What fraction is the translational kinetic energy of the total kinetic energy?
View SolutionA sphere of mass 50 gm and diameter 2 cm rolls without slipping with a velocfty of 5 cm/s. Calculate the total energy.
View SolutionThe radius of a sphere (in cm) whose volume is 12π cm3, is
View SolutionThe radius of a sphere is 1.23 cm. What is its surface area?
View SolutionA small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View Solution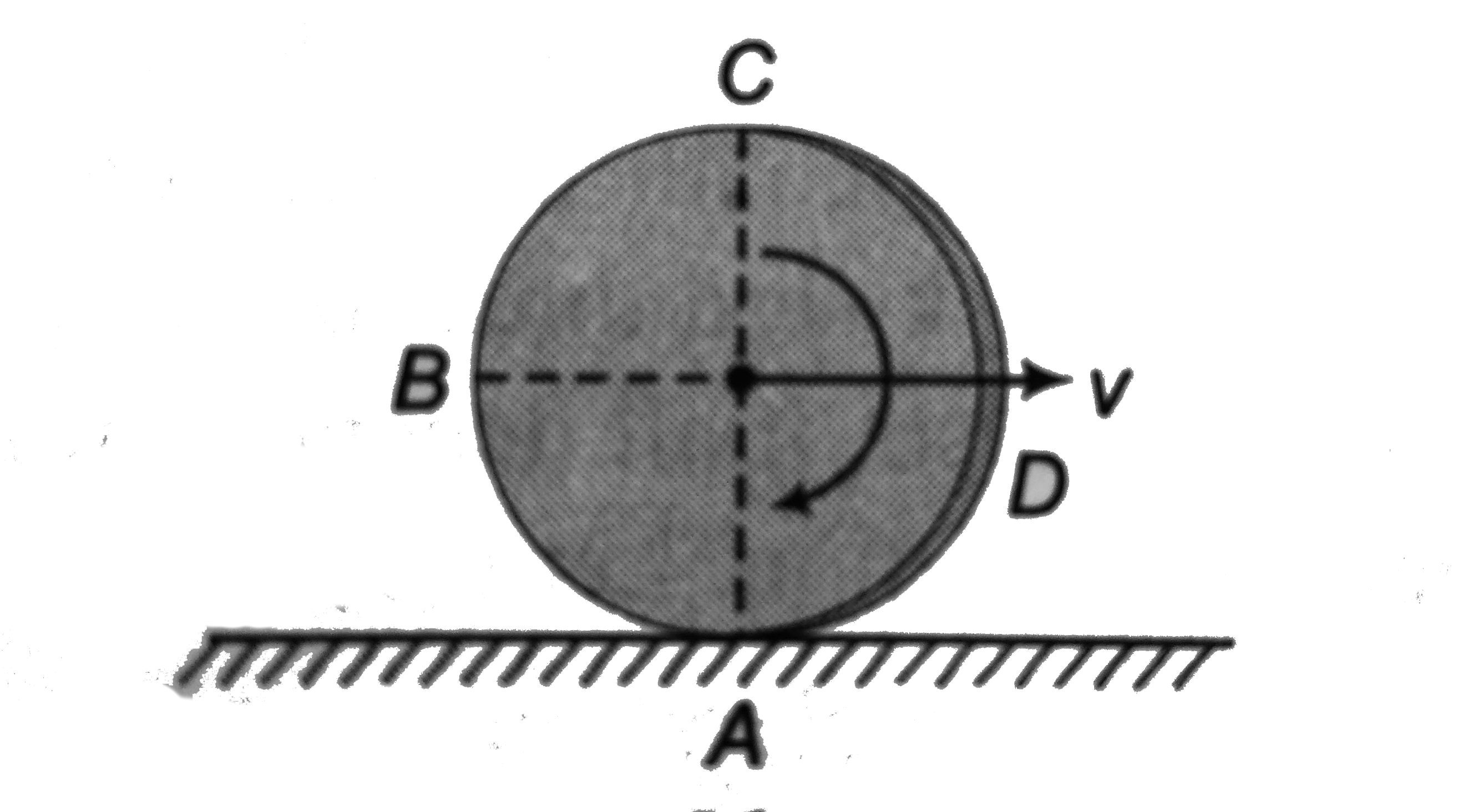
A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View Solution
