JEE Main And Advanced from SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) SIMPLE HARMONIC MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) | JEE Main And Advanced |
| Medium | English |
| Academic Year | 2023-2024 |
Question 9
A uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants k. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle (θ) in one direction and released. The frequency of oscillation is. ?
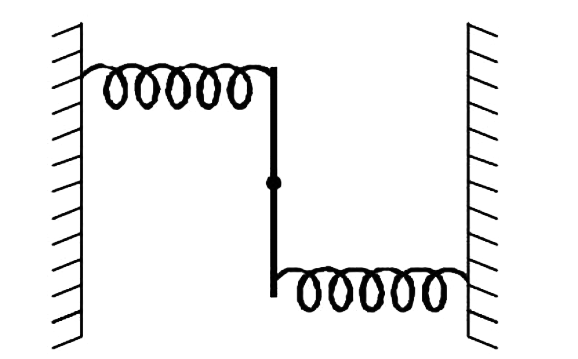 .View Solution
.View SolutionQuestion 12
A small block is connected to one end of a massless spring of un - stretched length 4.9m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2m and released from rest at t=0. It then executes simple harmonic motion with angular frequency (ω)=(π/3)rad/s. Simultaneously at t=0, a small pebble is projected with speed (v) from point (P) at an angle of 45∘ as shown in the figure. Point (P) is at a horizontal distance of 10momO. If the pebble hits the block at t=1s, the value of (v) is (takeg=10m/s2).
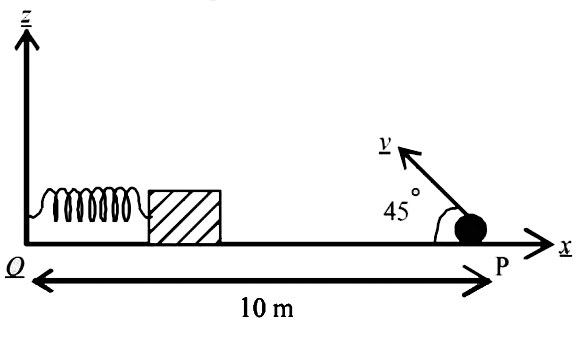 .View Solution
.View SolutionQuestion 15
A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.View SolutionQuestion 16
A highly rigid cubical block A of small mass M and slide L is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force F is applied perpendicular to one of the sides faces of A. After the force is withdrawn, block A executes small oscillations the time period of which is given by.View SolutionQuestion 17
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :View SolutionQuestion 21
A metal rod of length 'L' and mass 'm' is pivoted at one end. A thin disc of mass 'M' and radius R <L is attached at its center to the free end of the rod. Consider two ways the disc is attached : (case A). The dise is not free to rotate about its centre and (case B) the disc is free to rotate about its centre. The rod disc system perfoms (SHM) in vertical plane after being released from the same displacement position. Which of the following statement (s) is (are) true ?
 .View Solution
.View SolutionQuestion 23
A block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at x=x0+A. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?View SolutionQuestion 26
Two light springs of force constants (k_1 and k_2) and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block k1=1.8N/m,k2=3.2N/m,m=200gm).
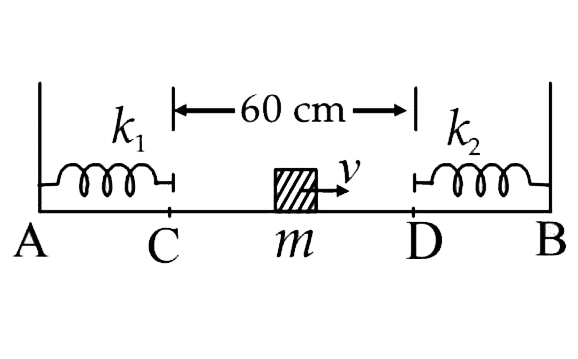 .View Solution
.View SolutionQuestion 27
Two non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
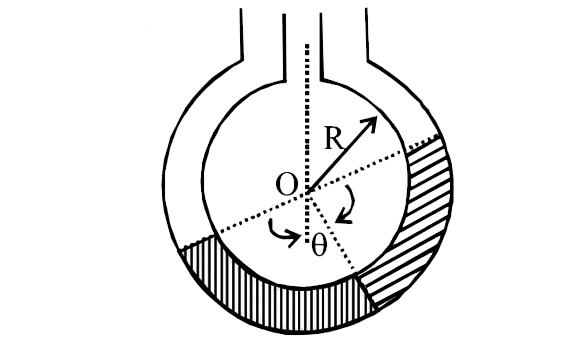 .
.
(a) Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
(b) If the whole is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the period of these oscillations.View SolutionQuestion 28
Two identical balls (A) and (B) each of mass (0.1 kg), are attached to two identical massless springs. The spring - mass system is constrained to move inside a riged smooth pipe bant in the form of a circle as shown in Fig. The pipe is fixed in a horizontal plane.
The centres of the balls can move in a circle of radius (0.06 pi) meter. Each spring has a natural length zof0.06π meter and spring spring constant5 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radian with respect to the diameter (pQ) of the circle (as shown in Fig.) and released from, rest.
 .
.
(i) Calculate the frequency of oscillation of ball (B).
(ii) Find the speed of ball (A) when (A) and (B) are at the two ends of the diameter (PQ).
(iii) What is the total energy of the system.View SolutionQuestion 29
A thin rod of length (L) and area of cross - section (S) is pivoted at its lowest point (P) inside a stationary, homegeneous and non - viscous liquid. The rod is free to ratate in a vertical plane about a horizontal axis passing through (P). The density (d_1) of the material of the rod is smaller than the density (d_2) of the liquid. The rod is displaced by a small angle (theta) from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
 .View Solution
.View SolutionQuestion 30
A small body attached to one end of a vertically hanging spring is performing (SHM) about is mean position with angular frequency (omega) and amplitude (a). If at a height (y*) from the mean position, the body gets detached from the spring, calculate the value of (y*) so that the height (H) attained by the mass is maximum. The body does noy interact with the spring during its subsquent motion after detachment. (aω2>g).
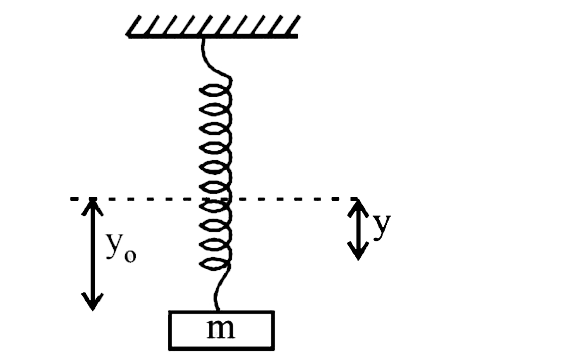 .View Solution
.View SolutionQuestion 31
When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0) (see figure).
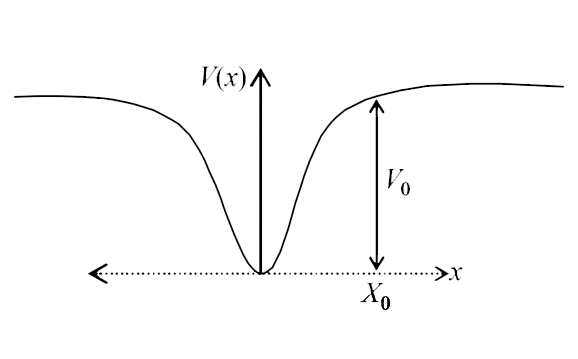
If total energy of the particle is E, it will perform perildic motion only if.View SolutionQuestion 32
When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0) (see figure).
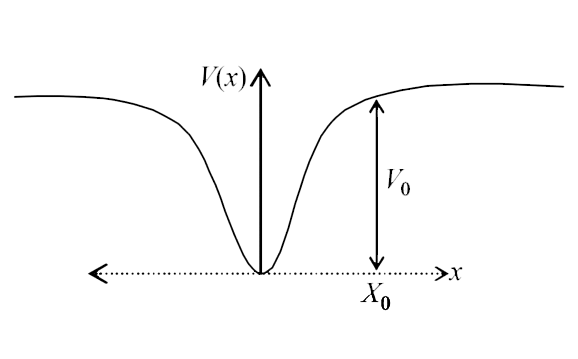 .
.
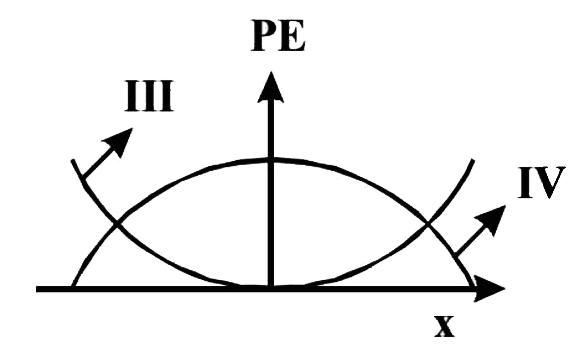
For periodic motion of small amplitude A,the time period (T) of thes particle is proportional to.View SolutionQuestion 33
When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0)(seefigure).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_CHMO_C10_033_Q01.pngwh=80%mx-autosty≤=background:white;>.<br>Theae≤rationofthisparti≤for|x|gtX_(0)is<br>(a)∝rtional→V_(0)
(b) proportional to.View SolutionQuestion 34
Phase space deagrams are useful tools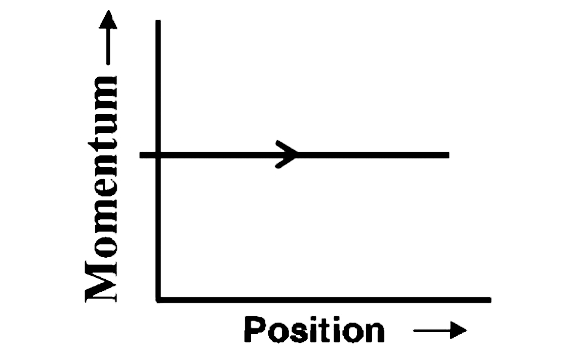 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
The phace diagram for a ball thrown vertically up from ground is.View SolutionQuestion 35
Phase space deagrams are useful tools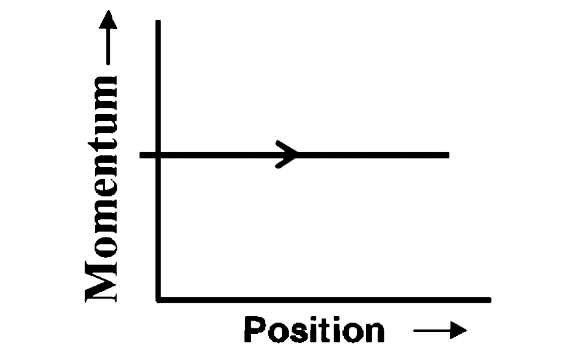 .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
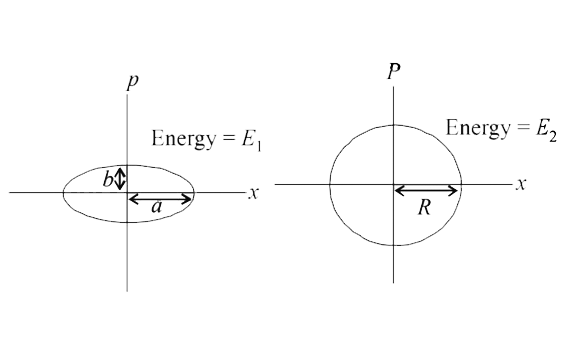
The plase space deagram for simple harmonic motion is a circle centered at the origin. In the figure, the two circles represent the same oscillator but for different initial condetions, and E_(1) and E_(2) the total mechanical energies respectivey.
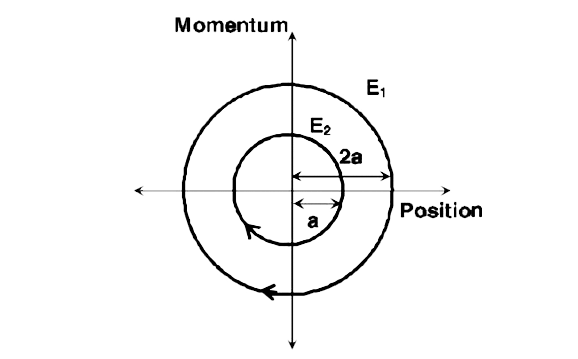 .View Solution
.View SolutionQuestion 36
Phase space deagrams are useful tools .
.
in analyzing all kinds of dynamical problems. They are especially usrful in studying the changes in motion as initial position and momenum are changed. Here we conseder some simple dynamical systems in one dimension. For such systems, phase space is a plane in which position is plotted along horizontal axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs. p(t) curve in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which positon or momentum upwards (or to right) is poitive and downwards (or to left) is negative.
Consider the spring-mass system, with mass submerged in water, as shown in the figure. The phase space diagram for one cycle of this system is.
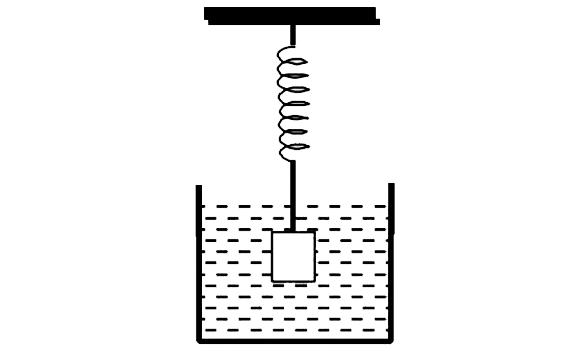 .View Solution
.View SolutionQuestion 45
The bob of a simple pendulum executm simple harmonic motion in water with a period t, while the period of oscillation of the bob is t0 in air. Negleting frictional force of water and given that the density of the bob is (4//3)xx1000 kg//m^(3).
What relationship between t and t0 is true.View SolutionQuestion 48
A particle of mass (m) is attached to a spring (of spring constant k) and has a narural angular frequency omega_(0). An external force R(t) proportional to cos omegat(omega!=omega)(0) is applied to the oscillator. The time displacement of the oscillator will be proprtional to.View SolutionQuestion 63
If a simple pendulum has significant amplitude (up to a factor of 1/e of original) only in the period between t = Os to t=τs, then τ may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds: View SolutionQuestion 65
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross - section area A. When the piston is in equilibrium, the volume of the gas is (V0) and the its pressure is (P0). The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, Show that the piston executes simple harmonic motion and find the frequency of oscillations. View Solution
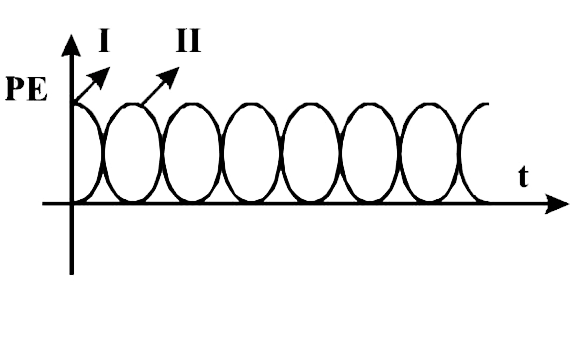 ,
,  .
. .
. .
.
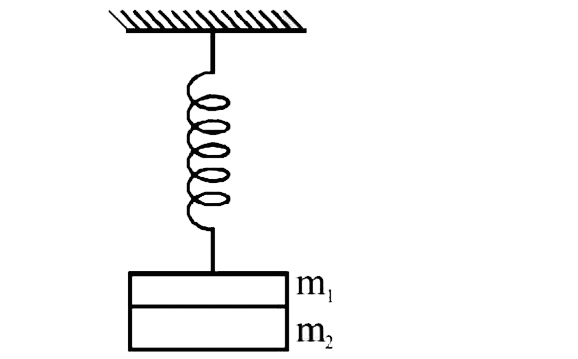 .
..</a><a href=) View Solution
View Solution