For Problems from CENGAGE PUBLICATION CIRCLE for Class 12

Class 12	MATHS
Chapter	CIRCLE
CENGAGE PUBLICATION	For Problems
Medium	English
Academic Year	2023-2024

Question 1
Each side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to $x + y = 0$ . Find the co-ordinates of the vertices of the square. View Solution
Question 2
Each side of a square has length 4 units and its center is at (3,4). If one of the diagonals is parallel to the line $y = x$ , then anser the following questions.
The radius of the circle inscribed in the triangle formed by any three vertices is View Solution
Question 3
Each side of a square has length 4 units and its center is at (3,4). If one of the diagonals is parallel to the line $y = x$ , then anser the following questions.
The radius of the circle inscribed in the triangle formed by any three vertices is View Solution
Question 4
Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?View Solution
Question 5
Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?View Solution
Question 6
Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?View Solution
Question 7
about to only mathematics View Solution
Question 8
Consider a family of circles passing through the point (3,7) and (6,5). Answer the following questions.
If each circle in the family cuts the circle $x^{2} + y^{2} - 4 x - 6 y - 3 = 0$ , then all the common chords pass through the fixed point which is View Solution
Question 9
Consider a family of circles passing through the point (3,7) and (6,5). Answer the following questions.
If the circle which belongs to the given family cuts the circle $x^{2} + y^{2} = 29$ orthogonally, then the center of that circle is (a) (1 / 2 , 3 / 2 ) (b) ( 9 / 2 , 7 / 2 ) (c) ( 7 / 2 , 9 / 2 ) (d) ( 3 , − 7 / 9 ) View Solution
Question 10
Consider the relation $4 l^{2} - 5 m^{2} + 6 l + 1 = 0$ , where l, m $\in R$ .
The line lx+my+1=0 touches a fixed circle whose equation is View Solution
Question 11
Consider the relation $4 l^{2} - 5 m^{2} + 6 l + 1 = 0$ , where $l, m \in R$
Tangents PA and PB are drawn to the above fixed circle from the points P on the line $x + y - 1 = 0$ . Then the chord of contact AP passes through the fixed point. (a) ( 1 / 2 , − 5 / 2 ) (b) ( 1 3 , 4 / 3 ) (c) ( − 1 / 2 , 3 / 2 ) (d) none of these View Solution
Question 12
Consider the relation $4 l^{2} - 5 m^{2} + 6 l + 1 = 0$ , where $l, m \in R$
The number of tangents which can be drawn from the point (2,-3) to the above fixed circle are View Solution
Question 13
A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that $Δ O A P$ is a right angled triangle at A and its perimeter is 8 units. The length of $Q P$ is View Solution
Question 14
A circle C whose radius is 1 unit touches the x-axis at point A. The center Q of C lies in the first quadrant. The tangent from the origin O to the circle touches it at T and a point P lies on its such that $Δ O A P$ is a right - angles triangle at A and its perimeter is 8 units.
The length of PQ is View Solution
Question 15
A circle C whose radius is 1 unit touches the x-axis at point A. The center Q of C lies in the first quadrant. The tangent from the origin O to the circle touches it at T and a point P lies on its such that $Δ O A P$ is a right - angles triangle at A and its perimeter is 8 units.
The length of PQ is View Solution
Question 16
P is a variable point of the line L = 0. Tangents are drawn to the circle $x^{2} + y^{2} = 4$ from P to touch it at Q and R. The parallelogram PQSR is completed. If $L = 2 x + y - 6 = 0$ , then the locus of circumcetre of $△ P Q R$ is -View Solution
Question 17
P is a variable point on the line $L = 0$ . Tangents are drawn to the circles $x^{2} + y^{2} = 4$ from P to touch it at Q and R. The parallelogram PQSR is completed.
If $P \equiv (6, 8)$ , then the area of $Δ Q R S$ is View Solution
Question 18
P is a variable point on the line $L = 0$ . Tangents are drawn to the circles $x^{2} + y^{2} = 4$ from P to touch it at Q and R. The parallelogram PQSR is completed.
If $P \equiv (3, 4)$ , then the coordinates of S are View Solution
Question 19
To the circle $x^{2} + y^{2} = 4$ two tangents are drawn from $P (- 4, 0)$ , which touch the circle at $T_{1}$ , and $T_{2}$ and a rhombus $P T_{1} P' T_{2}$ is completed. Circumcentre of the triangle $P T_{1} T_{2}$ is at View Solution
Question 20
To the circle $x^{2} + y^{2} = 4$ , two tangents are drawn from $P (- 4, 0)$ , which touch the circle at $T_{1}$ and $T_{2}$ . A rhomus $P T_{1} P' T_{2}$ s completed.
The circumcenter of triangle $P T_{1} T_{2}$ is at View Solution
Question 21
To the circle $x^{2} + y^{2} = 4$ , two tangents are drawn from $P (- 4, 0)$ , which touch the circle at $T_{1}$ and $T_{2}$ . A rhomus $P T_{1} P' T_{2}$ s completed.
If P is taken to be at (h,0) such that P' lies on the circle, the area of the rhombus is View Solution
Question 22
Let $α$ chord of a circle be that chord of the circle which subtends an angle $α$ at the center.
If $x + y = 1$ is a chord of $x^{2} + y^{2} = 1$ , then $α$ is equal to View Solution
Question 23
If $α -$ chord of a circle be that chord which subtends an angle $α$ at the centre of the circle.
If slope of $a \frac{π}{3}$ chord of $x^{2} + y^{2} = 4$ is 1, then its equaiton is View Solution
Question 24
If $α -$ chord of a circle be that chord which subtends an angle $α$ at the centre of the circle.
Distance of $\frac{2 π}{3} -$ chord of $x^{2} = y^{2} + 2 x + 4 y + 1 = 0$ from the centre is View Solution
Question 25
Two variable chords AB and BC of a circle $x^{2} + y^{2} = a^{2}$ are such that AB=BC=a, M and N are the mid-points of AB and BC respectively such that line joining MN intersect the circle at P and Q where P is closer to AB and O is the centre of the circle.
$∠ O A B$ is View Solution
Question 26
Two variable chords AB and BC of a circle $x^{2} + y^{2} = a^{2}$ are such that AB=BC=a, M and N are the mid-points of AB and BC respectively such that line joining MN intersect the circle at P and Q where P is closer to AB and O is the centre of the circle.
$∠ O A B$ is View Solution
Question 27
Two variable chords AB and BC of a circle $x^{2} + y^{2} = a^{2}$ are such that $A B = B C = a$ . M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is View Solution
Question 28
Given two circles intersecting orthogonally having the length of common chord $\frac{24}{5}$ unit. The radius of one of the circles is 3 units.
If radius of other circle is $λ$ units then $λ$ is View Solution
Question 29
Given two circles intersecting orthogonally having the length of common chord $\frac{24}{5}$ unit. The radius of one of the circles is 3 units.
If radius of other circle is $λ$ units then $λ$ is View Solution
Question 30
Given two circles intersecting orthogonally having the length of common chord $\frac{24}{5}$ unit. The radius of one of the circles is 3 units.
If radius of other circle is $λ$ units then $λ$ is View Solution
Question 31
In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio $5 : 3$

The radius of the circle with center B is View Solution
Question 32
In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio $5 : 3$

The radius of the circle with center B is View Solution
Question 33
In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio $5 : 3$

The radius of the circle with center B is View Solution
Question 34
Let the circles
$S_{1} \equiv x^{2} + y^{2} + 4 y - 1 = 0$
$S_{2} \equiv x^{2} + y^{2} + 6 x + y + 8 = 0$
touch each other . Also, let $P_{1}$ be the point of contact of $S_{1}$ and $S_{2}$ , $C_{1}$ and $C_{2}$ are the centres of $S_{1}$ and $S_{2}$ respectively.
The coordinates of $P_{1}$ are View Solution
Question 35
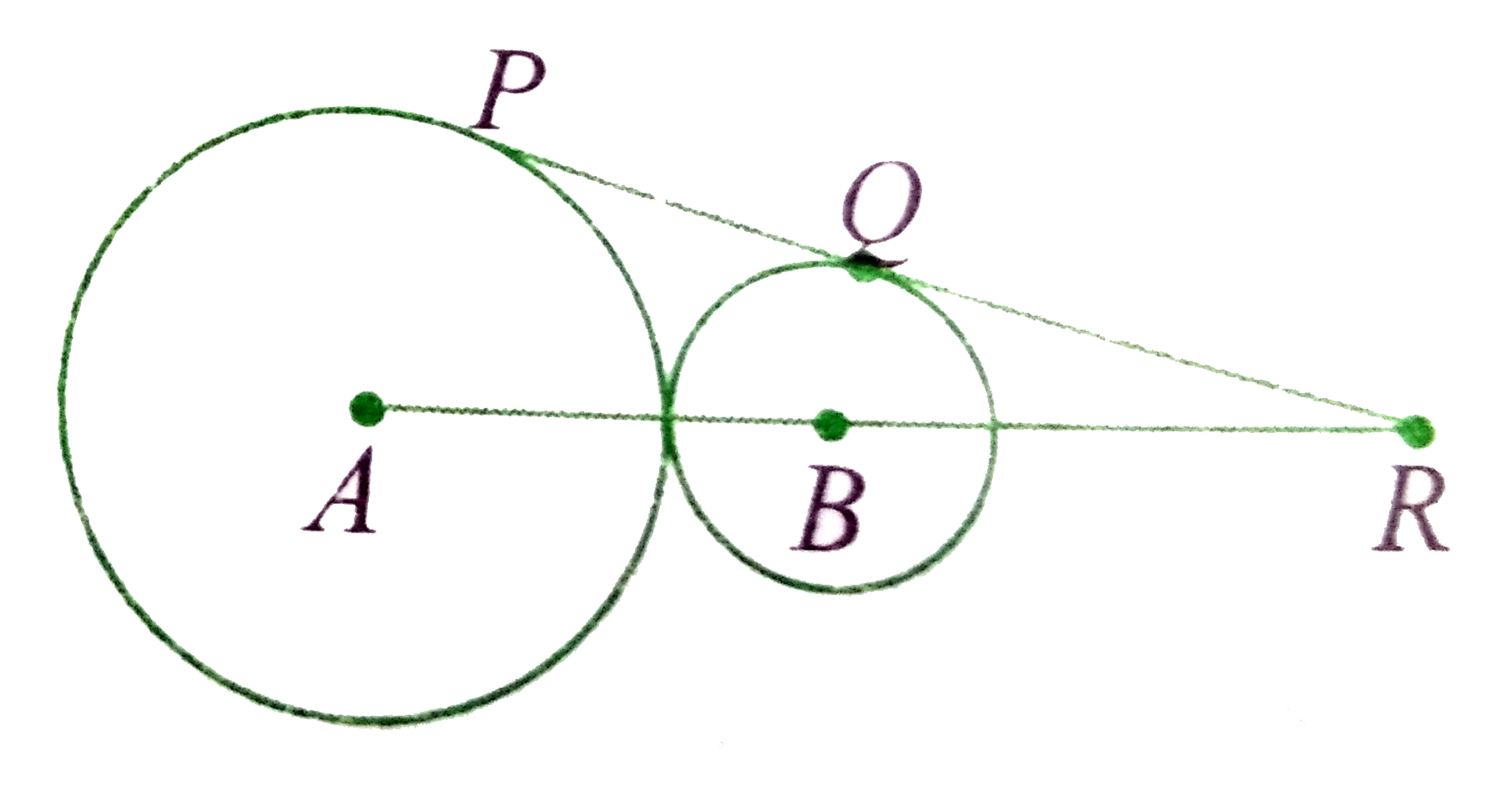
Let each of the circles
$S_{1} \equiv x^{2} + y^{2} + 4 y - 1 = 0$
$S_{1} \equiv x^{2} + y^{2} + 6 x + y + 8 = 0$
$S_{3} \equiv x^{2} + y^{2} - 4 x - 4 y - 37 = 0$
touch the other two. Also, let $P_{1}, P_{2}$ and $P_{3}$ be the points of contact of $S_{1}$ and $S_{2}, S_{2}$ and $S_{3}$ , and $S_{3}$ , respectively, $C_{1}, C_{2}$ and $C_{3}$ are the centres of $S_{1}, S_{2}$ and $S_{3}$ respectively.
The ratio $\frac{area (Δ P_{1} P_{2} P_{3})}{area (Δ C_{1} C_{2} C_{3})}$ is equal to View Solution
Question 36
Let each of the circles
$S_{1} \equiv x^{2} + y^{2} + 4 y - 1 = 0$
$S_{1} \equiv x^{2} + y^{2} + 6 x + y + 8 = 0$
$S_{3} \equiv x^{2} + y^{2} - 4 x - 4 y - 37 = 0$
touch the other two. Also, let $P_{1}, P_{2}$ and $P_{3}$ be the points of contact of $S_{1}$ and $S_{2}, S_{2}$ and $S_{3}$ , and $S_{3}$ , respectively, $C_{1}, C_{2}$ and $C_{3}$ are the centres of $S_{1}, S_{2}$ and $S_{3}$ respectively.
The ratio $\frac{area (Δ P_{1} P_{2} P_{3})}{area (Δ C_{1} C_{2} C_{3})}$ is equal to View Solution
Question 37
The line $x + 2 y + a = 0$ intersects the circle $x^{2} + y^{2} - 4 = 0$ at two distinct points A and B. Another line $12 x - 6 y - 41 = 0$ intersects the circle $x^{2} + y^{2} - 2 y + 1 = 0$ at two distinct point C and D.
The equation of the circle passing through the points A,B,D, and D is View Solution
Question 38
The line $x + 2 y = a$ intersects the circle $x^{2} + y^{2} = 4$ at two distinct points $A and B$ Another line $12 x - 6 y - 41 = 0$ intersects the circle $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$ at two $C and D$ . The value of 'a' for which the points $A, B, C and D$ are concyclic -View Solution
Question 39
Let A,B, and C be three sets such that
$A = {(x, y) ∣ \frac{x}{cos θ} = \frac{y}{sin θ} = 5, where' θ' is parameter}$
$B = {(x, y) ∣ \frac{x - 3}{cos ϕ} = \frac{y - 4}{sin ϕ} = r}$
$C = {(x, y) ∣ {(x - 3)}^{2} + {(y - 4)}^{2} \leq R^{2}}$
If $A \cap C = A$ , then minimum value of R is
(a)5
(b)6
(c)10
(d)11 View Solution
Question 40
Let A,B, and C be three sets such that
$A = {(x, y) ∣ \frac{x}{cos θ} = \frac{y}{sin θ} = 5, where' θ' is parameter}$
$B = {(x, y) ∣ \frac{x - 3}{cos ϕ} = \frac{y - 4}{sin ϕ} = r}$
$C = {(x, y) ∣ {(x - 3)}^{2} + {(y - 4)}^{2} \leq R^{2}}$
If $ϕ$ is fixed and r varies and $(A \cap B) = 1$ , then $sec ϕ$ is equal to (a) $\frac{5}{4}$ (b) $\frac{- 5}{4}$ (c) $\frac{5}{3}$ (d) $\frac{- 5}{3}$ View Solution
Question 41
Consider the family of circles $x^{2} + y^{2} - 2 x - 2 a y - 8 = 0$ passing through two fixed points A and B . Also, $S = 0$ is a cricle of this family, the tangent to which at A and B intersect on the line $x + 2 y + 5 = 0$ .
The distance between the points A and B , is View Solution
Question 42
Consider the family of circles $x^{2} + y^{2} - 2 x - 2 a y - 8 = 0$ passing through two fixed points A and B . Also, $S = 0$ is a cricle of this family, the tangent to which at A and B intersect on the line $x + 2 y + 5 = 0$ .
The distance between the points A and B , is View Solution
Question 43
Consider the family of circles $x^{2} + y^{2} - 2 x - 2 a y - 8 = 0$ passing through two fixed points A and B . Also, $S = 0$ is a cricle of this family, the tangent to which at A and B intersect on the line $x + 2 y + 5 = 0$ .
If the circle $x^{2} + y^{2} - 10 x + 2 y = c = 0$ is orthogonal to $S = 0$ , then the value of c is View Solution
Question 44
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation $\sqrt{3} x + y - 6 = 0$ and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are

A. $y = \frac{2}{\sqrt{3}} + x + 1, y = - \frac{2}{\sqrt{3}} x - 1$
B. $y = \frac{1}{\sqrt{3}} x, y = 0$
C. $y = \frac{\sqrt{3}}{2} x + 1, y = - \frac{\sqrt{3}}{2} x - 1$
D. $y = \sqrt{3} x, y = 0$ View Solution
Question 45
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation $\sqrt{3} x + y - 6 = 0$ and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are

A. $y = \frac{2}{\sqrt{3}} + x + 1, y = - \frac{2}{\sqrt{3}} x - 1$
B. $y = \frac{1}{\sqrt{3}} x, y = 0$
C. $y = \frac{\sqrt{3}}{2} x + 1, y = - \frac{\sqrt{3}}{2} x - 1$
D. $y = \sqrt{3} x, y = 0$ View Solution
Question 46
A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation $\sqrt{3} x + y - 6 = 0$ and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are

A. $y = \frac{2}{\sqrt{3}} + x + 1, y = - \frac{2}{\sqrt{3}} x - 1$
B. $y = \frac{1}{\sqrt{3}} x, y = 0$
C. $y = \frac{\sqrt{3}}{2} x + 1, y = - \frac{\sqrt{3}}{2} x - 1$
D. $y = \sqrt{3} x, y = 0$ View Solution

All Exercises from CENGAGE PUBLICATION Class 12 MATHS CIRCLE

Home
Ask Doubt
Profile