There are two infinite slabs of charge, both of thickness d with the junction lying on the plane x = 0. The slab lying in the range 0 lt x lt d has a uniform charge density and the slab lying in the region – d lt x lt 0 has uniform charge density . Find the Electric field everywhere and plot its variation along the x axis. Note: This can be used to model the variation of electric field in the depletion layer of a p – n junction.
The correct Answer is:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
Consider two slabs of current shown in the figure. Both slabs have thickness b in y direction and extend up to infinity in x and z directions. The common face of the two slabs is y=0 plane. The slab in the region 0<y<d has a constant current density =J0ˆk and the other slab in the region –d<y<0 has a constant current density =J0(–ˆk).
(a) Find magnetic field at y=0
(b) Plot the variation of magnetic field (B) along the y axis.

View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane.
View SolutionA sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric field inside the sphere is
View SolutionAn infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ is given in which left half og the sheet contains charge density ρ and right half contains charge density. Find the electric field at the symmetry plane of this sheet
View SolutionAn infinitely thin straight wire has uniform linear charge density λ . Obtain the expression. For the electric field (E) at a point lying at a distance x from the wire, using Gauss' law.
(b) Show graphically the variation of this electric field E as a function of distance x from the wire .
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View SolutionA continuous line of charge of length 3d lies along the x-axis, extending from x + d to x + 4d, The line carries a uniform linear charge density lambd . In terms of d,λ and any necessary physical constant find the magnitude of the electric field at the origin.
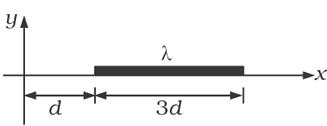
View SolutionA continuous line of charge of length 3d lies along the x-axis, extending from x + d to x + 4d, The line carries a uniform linear charge density lambd . In terms of d,λ and any necessary physical constant find the magnitude of the electric field at the origin.
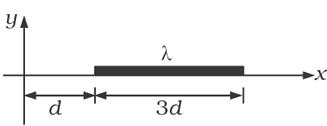
View SolutionWhat is potential at a distance r(<R) in a dielectric sphere of uniform charge density ρ, radius R and dielectric constant εr.

View SolutionWhat is potential at a distance r(<R) in a dielectric sphere of uniform charge density ρ, radius R and dielectric constant εr.
View Solution
