Subjective from CENGAGE PHYSICS (ENGLISH) Chapter 9 ELECTRIC POTENTIAL for Class 12
| Class 12 | PHYSICS |
| Chapter | ELECTRIC POTENTIAL |
| CENGAGE PHYSICS (ENGLISH) | Subjective |
| Medium | English |
| Academic Year | 2023-2024 |
Question 5
Water from a tap, maintained at a costant potential V, is allolwed to fall by drops of radius r through a small hole into a hollow conducting sphere of radius R standing on an insulating stand until it fills the entire sphere. Find the potential of the hollow conductor after it is completely filled with water.View SolutionQuestion 7
Figure shows a large conducting ceiling having uniform charge particle of charge density σ below which a charge particle of charge q0 and mass m is hung from point O, through a small string of length l. Calculate the minimum horizontal velocity v required for the string to become horizontal.
 .View Solution
.View SolutionQuestion 8
A nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
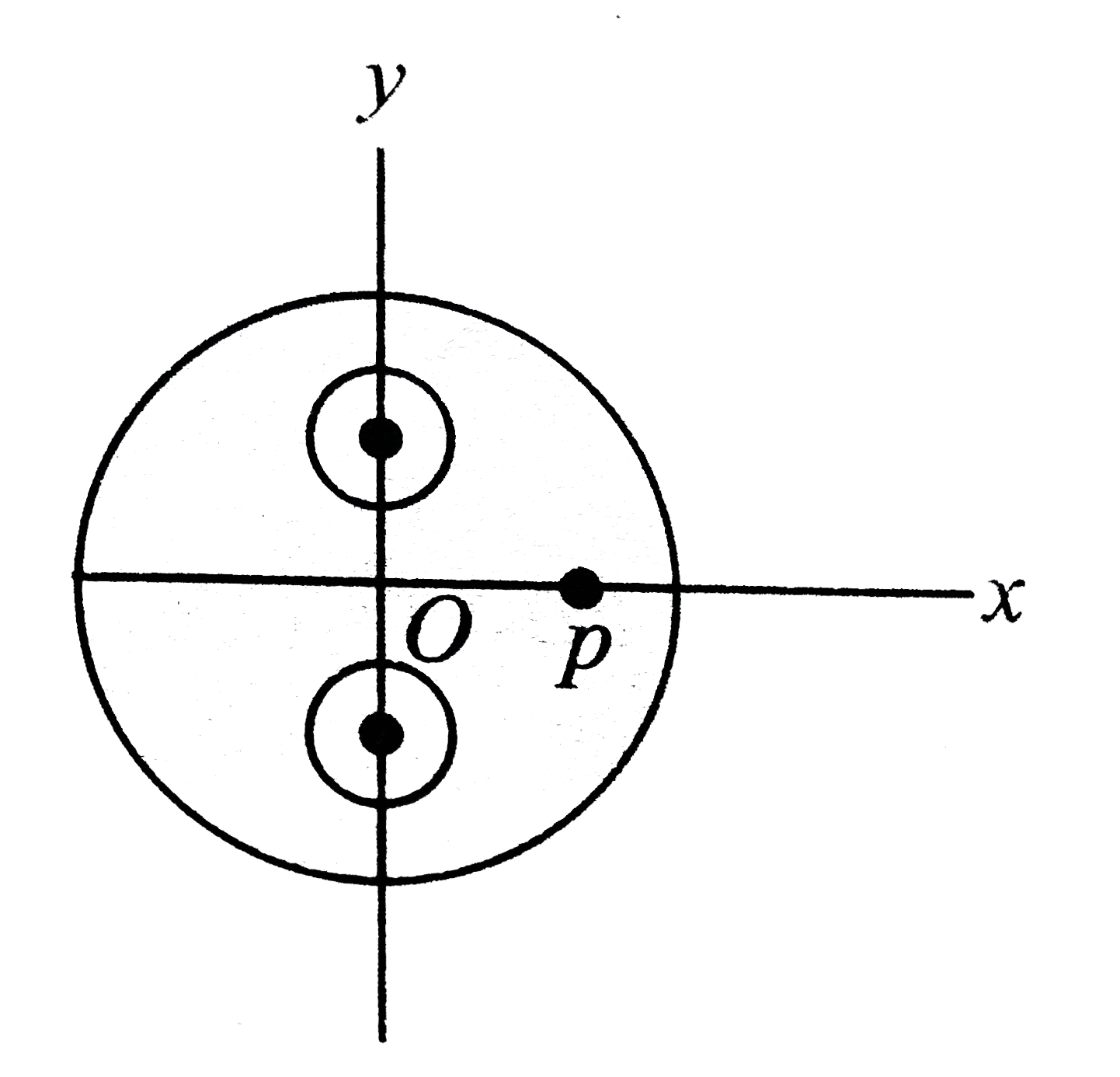 .View Solution
.View SolutionQuestion 10
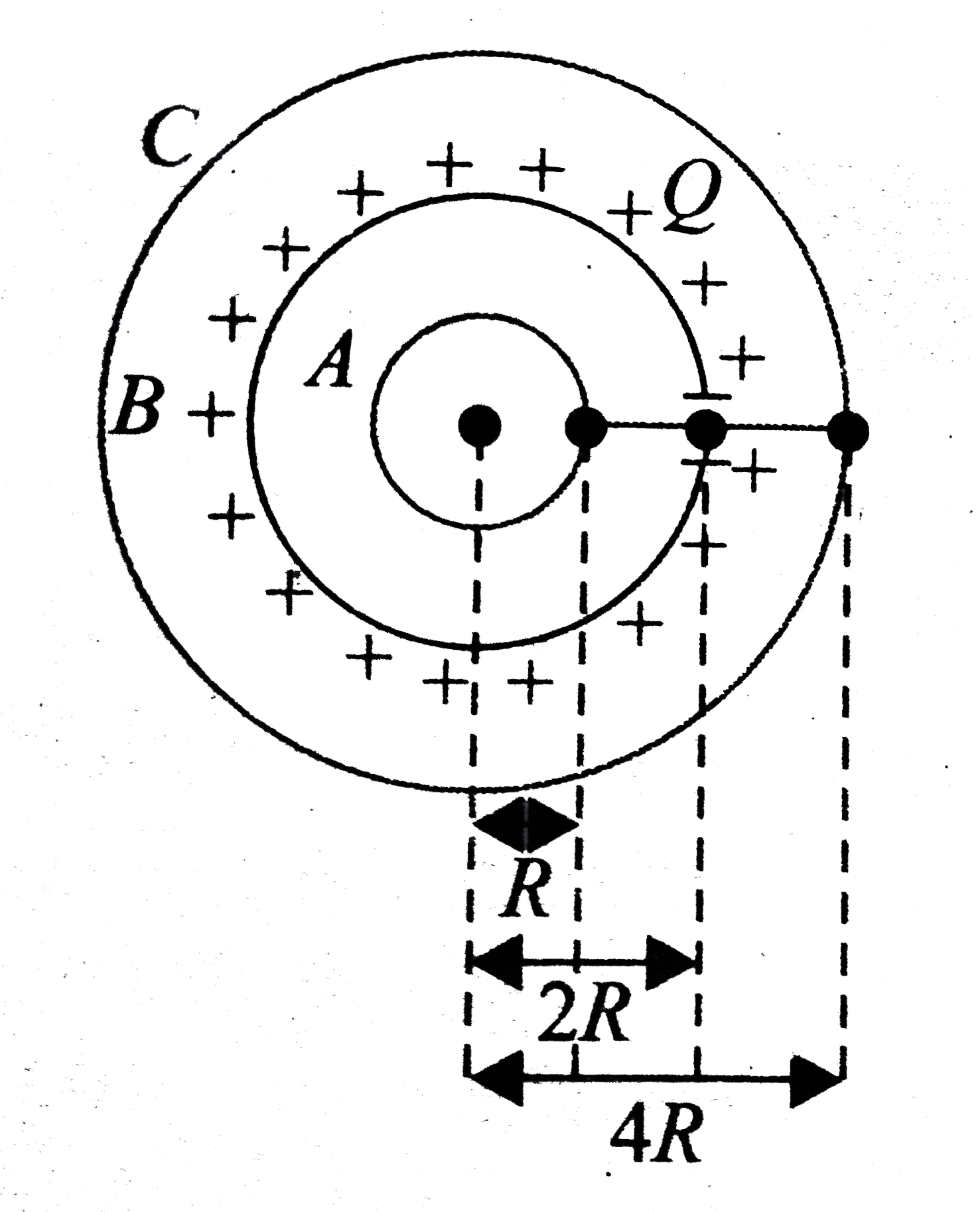
Three conducting spherical shells have radii (a, b, and c) such that a<b<c (Fig. 3.113). Initially, the inner shell is uncharged, the middle shell has a positive charge Q, and the outer shell has a negative charge −Q.
 .
.
a. Find the electric potential of the three shells.
b. If the inner and outer shells are now connected by a wire that is insulated as it passes through the middle shell, what is the electric potential of each of the three shells ? Also, what is the final charge on each shell ?View SolutionQuestion 12
Two concentric shells of radii R and 2R are shown in (Fig. 3.115). Initially, a charge q is imparted to the inner shells. Now, key K1 is closed and opened and then key K2 is closed and opened. After the keys K1andK2 are alterbately closed n times each, find the potential difference between the shells. Note that finally key K2 remains closed.
 .View Solution
.View SolutionQuestion 13
Three charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the center of the triangle.
a. Find the net force on charge q.
b. If Q=−q, will the charges at the corners move toward the center or fly away from it ?
c. For what value of Q at O will the charges remain stationary ?
d. In situation (c), how much work is done in removing the charges to infinity?View SolutionQuestion 14
A small ball of mass 2×10−3kg, having a charge 1μC, is suspended by a string of length 0.8m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution.View SolutionQuestion 16
A point charge q is located at the centre O of a spherical uncharged coducting layer provided with small orifice. The inside and outside radii of the layer are equal to a and b respectively. The amount of work that has to be performed to slowly transfer the charge q from teh point O through the orifice and into infinity is
 View Solution
View SolutionQuestion 17
Four point charges +8μC−1μC,−1μCand+8μC are fixed at the points −√27/2m,−√3/2m+√3/2mand+√27/2m respectively on the Y-axis. A particle of mass 6×10−4 kg and charge +0.1μC moves along the -X direction. It speed at x=+∞ is v0. Find the least value of v0 for which the paticle will cross the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free.View SolutionQuestion 19
Two uniformly charged large plane sheets S1 and S2 having charge densities σ1 and σ2 (σ1>σ2) are placed at a distance d parallel to each other. A charge q0 is moved along a line of length a(altd) at an angle 45∘ with the normal to S1. Calculate the work done by the electric fieldView SolutionQuestion 22
A short dipole is placed along the x - axis at x=x (Fig. 3.120).
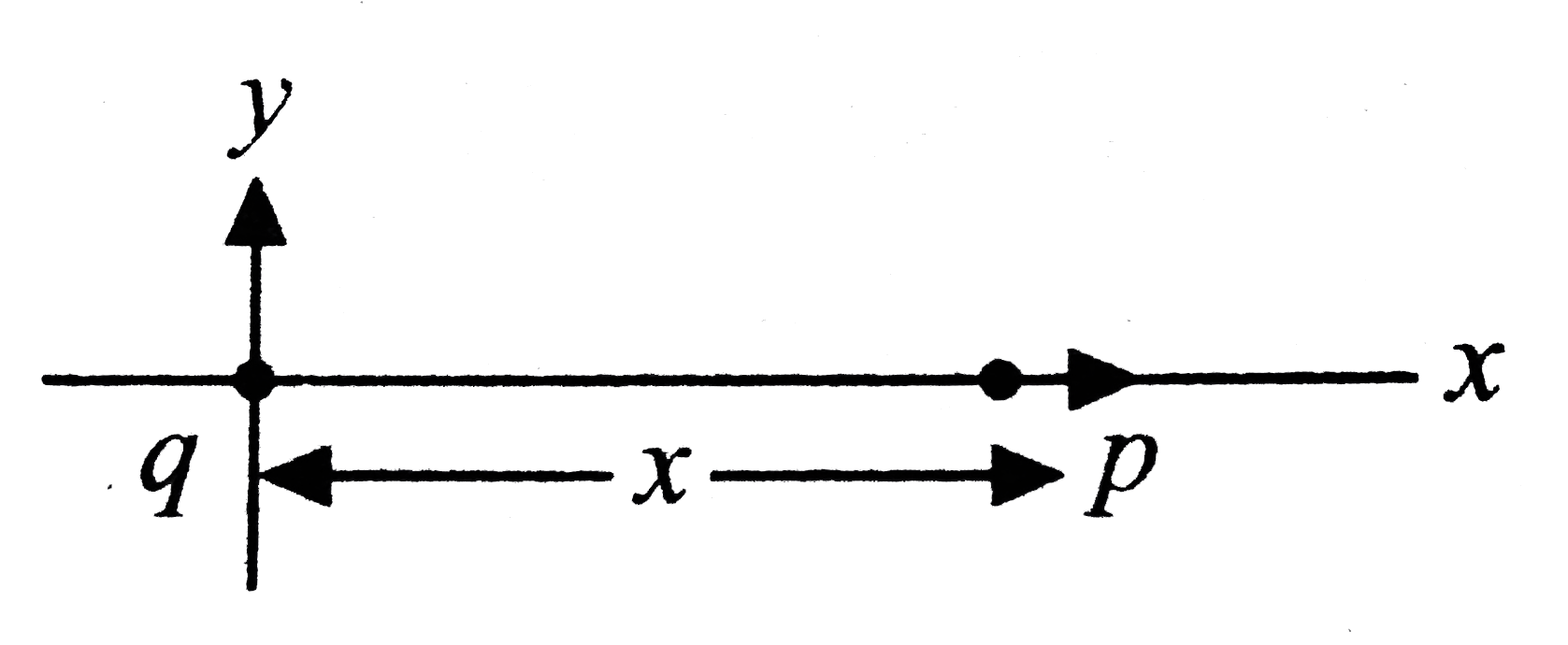 .
.
a. Find the force acting on the dipole due to a point charge q placed at the origin.
b. Find the force on the dipole if the dipole is rotated by 180∘ about the z- axis.
c. Find the force on dipole if the dipole is rotated by 90∘ anticlockwise about z - axis, i.e., it becomes parallel to the y - axis.View SolutionQuestion 24
Four charge particles each having charge Q=1 C are fixed at the corners of the base(A,B,C, and D) of a square pyramid with slant length a(AP=BP=PC=a=√2m), a charge -Q is fixed at point P. A dipole with dipole moment p=1 C-m is placed at the center of the bases and perpendicular to its plane as shown in fig. Force on the dipole due to the charge particles is □4πε0N.
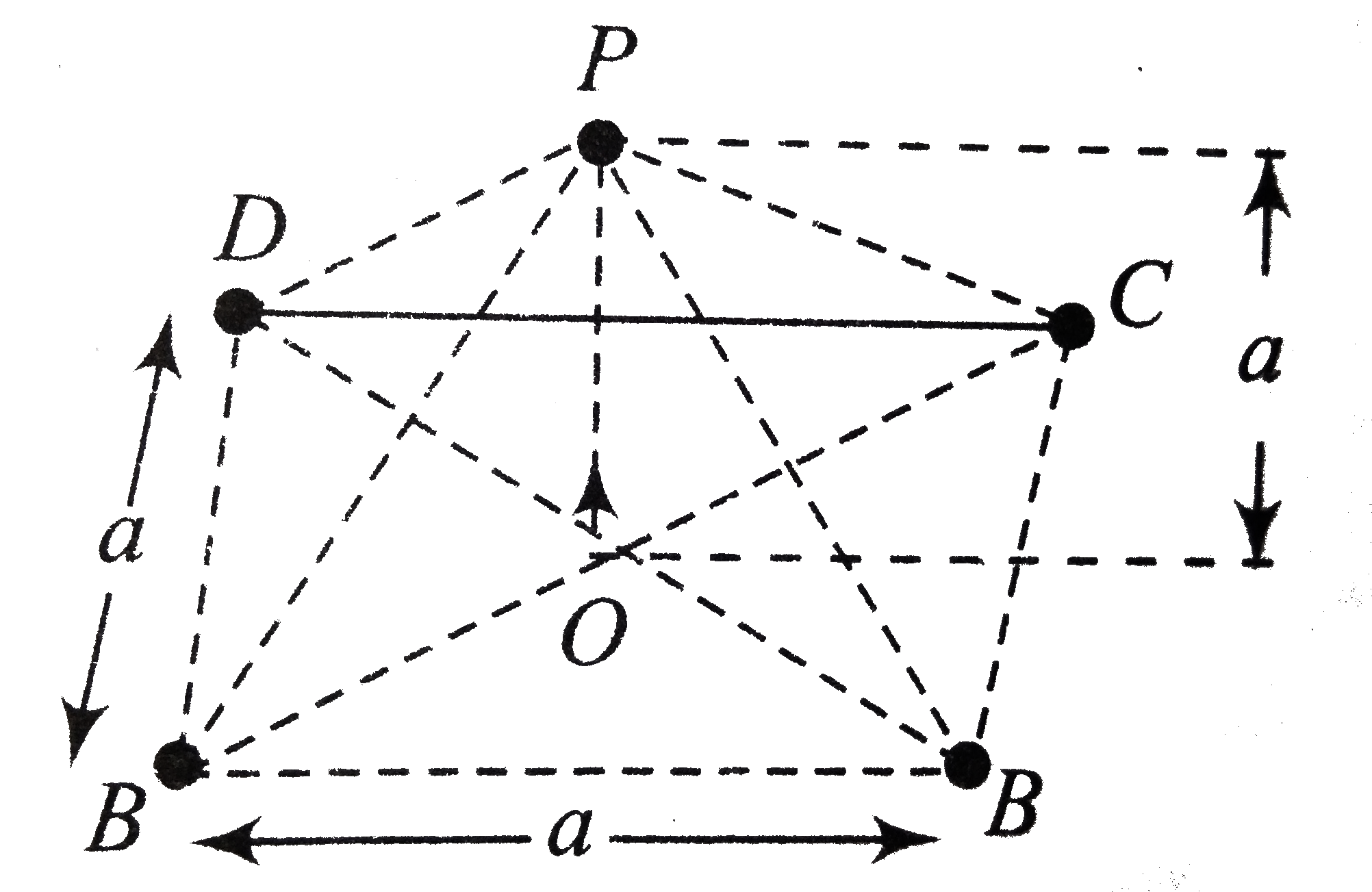 View Solution
View SolutionQuestion 26
A radioactive source, in the form of a metallic sphere of radius 10−2m emits β−particles at the rate of 5×1010 particles per second. The source is electrically insulated. How long will it take for its potential to be raised by 2V, assuming that 40% of the emitted β−particles escape the source.View SolutionQuestion 28
When a small uncharged conducting ball of radius a=1cm and mass m=50g is dropped from a height h above the center of another large conducting sphere of radius b(=1m) having charge Q(=(100μC). It rises to a height h1(=2m) after the collision. Find the value of h. Assume that during the impact there is no dissipation of energy.
 .View Solution
.View Solution
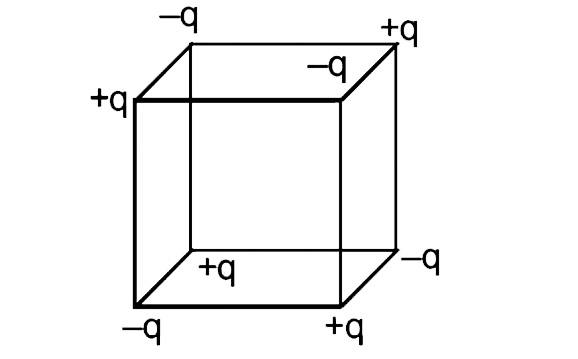
 .
. .
. 
 .
. .
.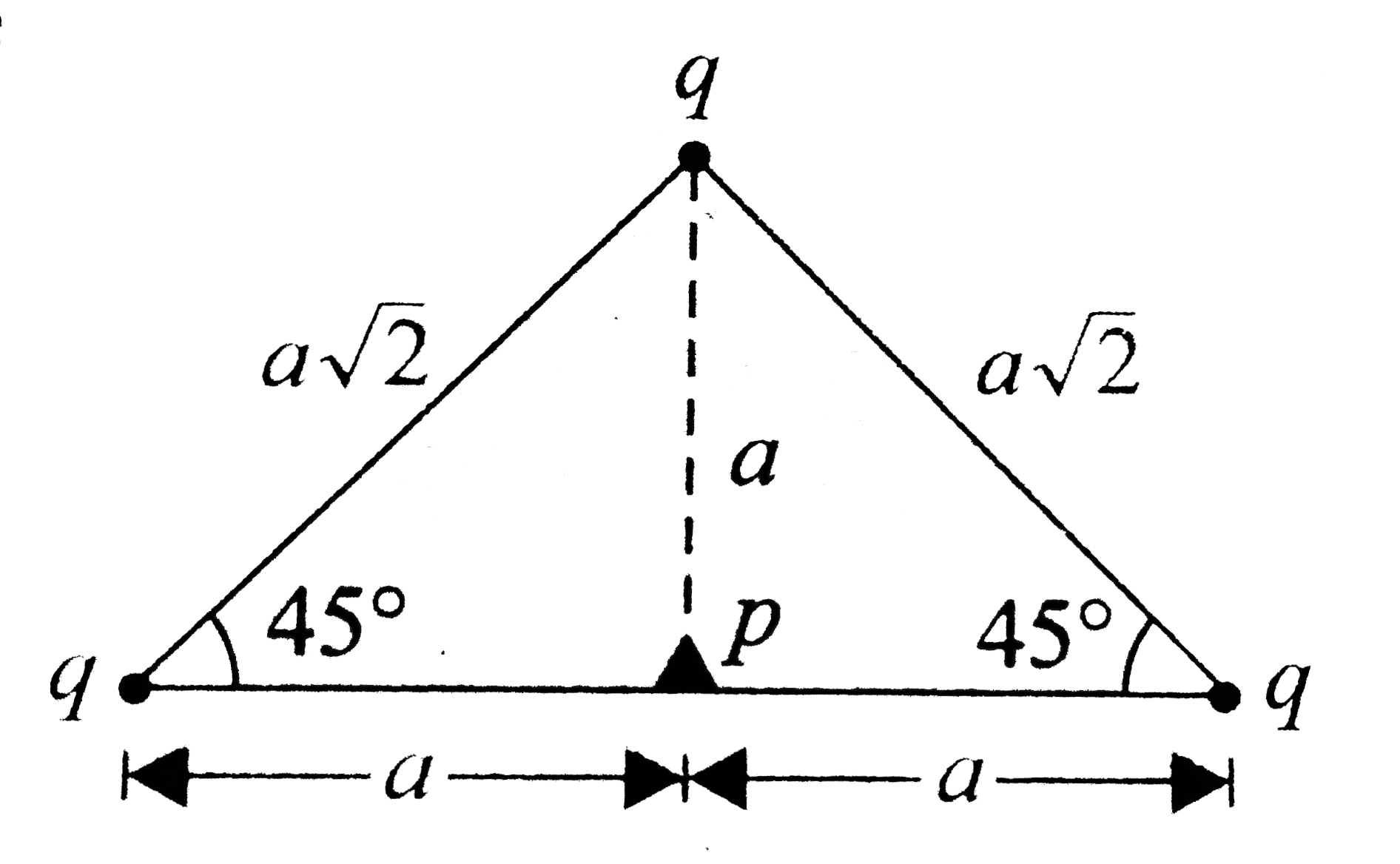 .
. 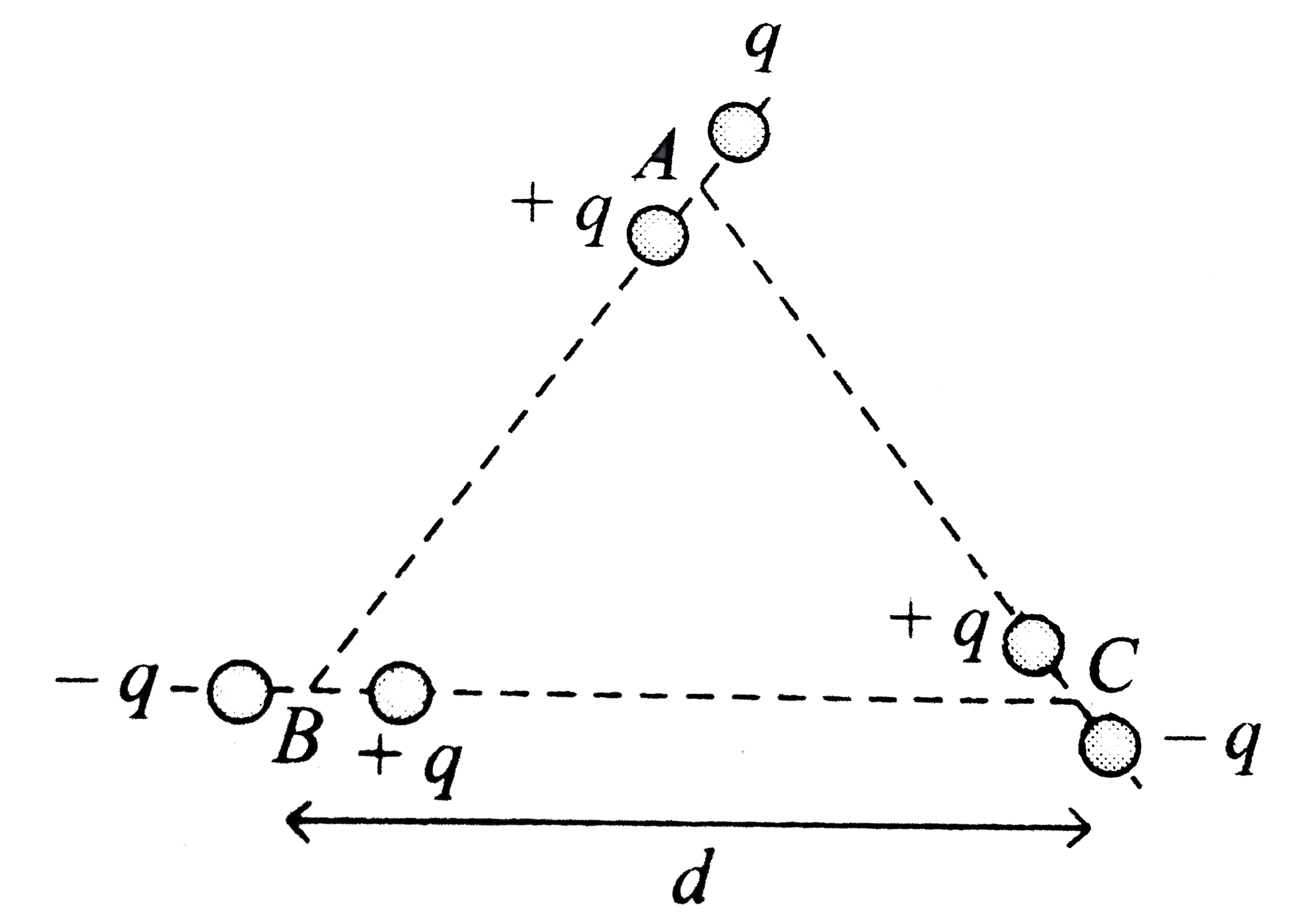 .
.