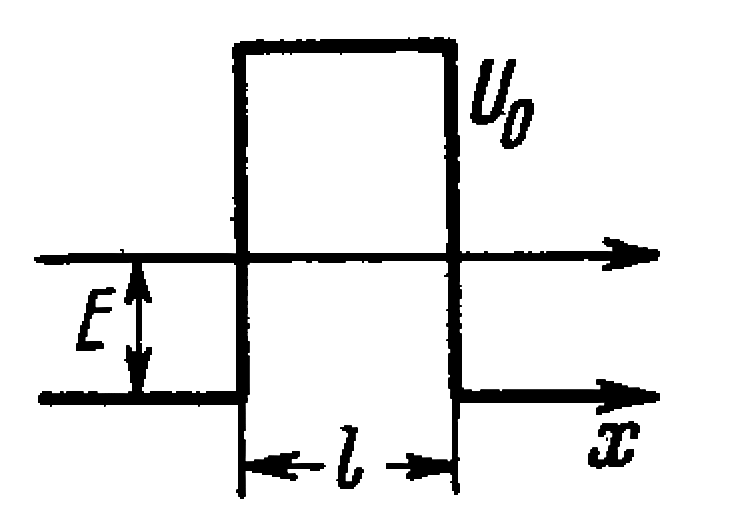Wave Properties Of Particle from IE IRODOV PHYSICS Chapter 1 ATOMIC AND NUCLEAR PHYSICS for Class 12

Class 12	PHYSICS
Chapter	ATOMIC AND NUCLEAR PHYSICS
IE IRODOV PHYSICS	Wave Properties Of Particle
Medium	English
Academic Year	2023-2024

Question 1
Calculate the de Broglie wavelength of an electron, proton and uranium atom, all having the same kinetic energy $100 e V$ .View Solution
Question 2
What amount of energy (in eV) should be added to an electron to reduce its de-Broglie its de-Broglie wavelength from 100 to 50 pm? Given $h = 6.62 \times 10^{- 34} J s, m_{e} = 9.1 \times 10^{- 31} k g$ .View Solution
Question 3
A neutron with kinetic energy $T = 25 e V$ strikes a stationary deuteron (heavy hydrogen nucleus). Find the de Broglie wavelength of both particles in the frame of their centre of intertia.View Solution
Question 4
Two identical non-re,aticivistic particles move at right angle to each other. Possesing de Broglie wavelength $λ_{1}$ and $λ_{2}$ Find the Broglie wavelength of each particle in the frame of their centre of inertia.View Solution
Question 5
Find the de Broglie wavelength of hydrogen molecules, which corresponds to their most probable velocity at room temperature.View Solution
Question 6
Calculate the most probable de Broglie wavelength of hydrogen molecules being in thermodynamics equilibrium at room temperature.View Solution
Question 7
Derive the expression for a due Broglie wavelength $λ$ of a relativistic particle moving with kinetic energy $T$ . At what value of $T$ does the error in deremining $λ$ using the non-relativistic forumula not exceed $1 %$ for an electron and a proton?View Solution
Question 8
At what value of kinetic energy is the de Broglie wavelength of an electron equal to its Compton wavelength?View Solution
Question 9
Find the de Broglie wavelength of relaativistic electrons reaching the anticathode of an $X$ -ray tube if the short wavelength limit of the continous $X$ -rays spectrum is equal to $λ_{s h} = 10.0 p m$ ?View Solution
Question 10
A parallel stream of monoenergetic electrons falls normally on a diaphragm with narrow square slit of width $b = 1.0 μ m$ . Find the velocity of the electrons if the width of the central diffraction maximum formed on a screen located at a distance $l = 50 c m$ from the slit is equal to $Δ x = 0.36 m m$ .View Solution
Question 11
A parallel stream of electrons accelerated by a potential difference $V = 25 V$ falls normally on a diaphragm with two narrow slits separated by a distance $d = 50 μ m$ . Calculate the distance betweeb neighbouring maxima of the diffraction patterns on a screen located at a distance $= 100$ cm from the slits. View Solution
Question 12
A narrow stream of monoenrgetic electrons falls at an angle of incidence $θ = 30^{\circ}$ on the natural facet of a n aluminum single crystal. The distacne between the neighbouring cystal planes parallel to that fact to $d = 0.20 n m$ . Theaximum mirror reflection is observed at a certain accelecrating voltage $V_{0}$ . Find $V_{0}$ if the next maximum mirror reflection is known to be observed when the acceleration voltage is increased $η = 2.25 t i m e s$ View Solution
Question 13
A narrow beam of monoenergetic electrons falls normally on the surface of a $N i$ single crystal. The reflection maximum of fourth order is observed in the direction forming an anle $θ = 55^{\circ}$ with the normal to the surface at the energy of the electrons equal to $T = 180 e V$ . Calcualte the corresponding value of the interplanar distance.View Solution
Question 14
A narrow stream of electrons with kinetic enrgy $T = 10 k e V$ passes through a polycrystalline aluminium foil, forming a system of diffraction fringes on a screen. Calculate tha interplanar distacne corresponding to the reflection of third order from a certain system of crystal planes if it is responsible for a diffraction ring of diameter $D = 3.20 c m$ . The distacnce between the foil and the screen is $l = 10.0 c m$ .View Solution
Question 15
A stream of electrons accelerated by a potential difference $V$ falls on the surface of a metal whose inner potential is $V_{i} = 15 V$ . Find:
(a) the refractive index of the metal for the electrons accelerated by a potential difference $V = 150 V$ ,
(b) the values of the raito $V / V_{i}$ at which the refracticve index differs from unity by not more than $η = 1.0 %$ .View Solution
Question 16
A particle of mass $m$ is located in a unidimensional square potential well with infinitely high walls. The width of the well is equal to $l$ . Find the permitted values of energy of the particle taking into accoint that only those states of the particle's motion are realized for which the whole number of de Broglie half waves are fitted within the given well.View Solution
Question 17
Describe the Bohr quantum conditions in terms of the wave theory: demonstrate that an electron in a hydrogen atom can move only along those round orbits which accommodate a whole number of de Broglie waves.View Solution
Question 18
Estimate the minimum errors in determining the velocity of an electron, a proton, and a ball of mass of $1 m g$ if the coordinates of the particles and of the centre of the ball are known with uncertainly $1 μ m$ .View Solution
Question 19
Employing the uncertainty principle, evaluate the indetreminancy of the velocity of an electron in a hydrogen atom if the size of the atom is assumed to be $l = 0.10 n m$ . Compare the obtained magnitude with the velocity of an electron in the first Bohar orbit of the given atom.View Solution
Question 20
Show that for the particle whose coordinate incertainty is $Δ x = λ / 2 π$ , where $λ$ is its de Broglie wavelength, the velocity uncertainty is of the same order of magnitude as the particle's velocity itself. View Solution
Question 21
A free electron was initially confined within a region with linear dimensions $l = 0.10 n m$ . Using the uncertinty principle evaluate the time over which the width of the corresponding trin of waves becomes $η = 10 t i m e s$ as large.View Solution
Question 22
Employing the uncertainty principle, estimate the minimum kinetic energy of an electron confined within a region whose sizes is $l = 0.20 n m$ .View Solution
Question 23
An electron with kinetic energy $T \approx 4 e V$ is confirned within a region whose linear dimension is $l = 1 μ m$ . Using the uncertianty principle, evaluate the relative uncertainty of its velocity.View Solution
Question 24
An electron is located in a unidimensional square potential well with infinitely high walls. The width of the well is $l$ . From the uncertainty principle estimate the force with which the electron possessing the minimum permitted energy acts on the walls of the well.View Solution
Question 25
A particle of mass $m$ moves in a unidimensional potential field $U = k x^{2} / 2$ (harmonic oscillator). Using the uncertainty principle, evaluate the minimum permitted energy of the particle in that field.View Solution
Question 26
Making use of the uncertainty principle,evaluate the minimum permitted energy of an electron in a hydrogen atom and its corresponding apparent distance from the nucleus.View Solution
Question 27
A parallel stream of hydrogen atoms with velocity $v = = 600 m / s$ falls normally on a diaphragm with a narrow slit behind which a screen is placed at a distance $l = 1.0 m$ . Using the uncertainty principle, evaluate the width of the slit $δ$ at which the width of its image on the screen is minimum.View Solution
Question 28
Find the particular solution of the time dependet Schrodinger equation for a freely moving particle of mass $m$ .View Solution
Question 29
A particle in the ground state is located in a unidimesional square potential well of length $l$ with absolutely impenetrable walls $(0 < x < l)$ . Find the probability of the particle staying within a region $\frac{1}{3} l \leq x \leq \frac{2}{3} l$ .View Solution
Question 30
A particle is located in a unidimensional square potential well with infinitely high wall. The width of the well is $l$ . Find the normalized wave fucntions of the stationary states of the particle taking the midpoint of the well for the origin of the $x$ coordinate.View Solution
Question 31
Demonstrate that the wave functions of the stationary states of a particle confined in a unidimensional potential well with infinitely high walls are orthogonal i.e., they satisfy the conditions
$\int_{0}^{l} ψ_{n} ψ_{n}, d x = 0$ if $n' \neq n$ . Here $l$ is thewidth of the well , $n$ are integers.View Solution
Question 32
A electron is located in unidimensional square potential well with infinitely high walls. The width of the well equal to $l$ is such that energy level is very dense. Find the density of the energy levels $d N / d E$ ,i.e., their number per unit energy interval,as a function of $E$ . Calculate $d N / d E$ for $E = 1.0 e V$ if $l = 1.0 c m$ .View Solution
Question 33
A particle of a mass $m$ is located in a two-diamensional square potential well with absolutely impenetrable walls. Find:
(a) the particles permitted energy values if the sides of the well are $l_{1}$ and $l_{2}$
(b) the energy values of the particle at the first four levels if the well has the shape of a square with side $l$ .View Solution
Question 34
A particle is located in a two-dimensional square potential well with absolutely impenetrable walls $(0 < x < a, 0 < y < b)$ . Find the probability of the particle with the lowesr energy to be located with in a region $0 < x < a / 3$ View Solution
Question 35
A particle of a mass $m$ is located in a three-dimensional cubic potential well with absoulutely impenetrable walls. The side of the cube is equal to $a$ Find:
(a) the proper value of the energy of the particel,
(b) the energy difference between the third and fourth levels,
(c )the energy of the sixth level and the number of states (the degree of degeneracy) corresponding to that level.View Solution
Question 36
Using the Schrodinger equation, demonstrate that at the point where the potential energy $U (x)$ of a particle has a infinte discountinuity, the wave function renains smooth, I.e., its first derivaltive with respect to the coordinate is continuous.View Solution
Question 37
A particle of mass $m$ is located in a unidimensional potential field $U (x)$ whose shape is shown in fig. where $U (0) = \infty$ . Find

(a) the equation defining the possible values of enrgy of the particle in the region $E < U_{0}$ , reduce taht equation to the from
$sin k l = \pm k l \sqrt{ħ^{2} / 2 m l^{2} U_{0}}$ ,
where $k = \sqrt{2 m E / ħ}$ . Solving this equation by graphical means, domonstrate that hte possible values of energy of the particle from a discontinuous spectrum,
(b)the minium value of the quantity $l^{2} U_{0}$ at which the first energy level appears in the region $E < U_{0}$ . At what minimum value of $l^{2} U_{0}$ does the nth level appear?View Solution
Question 38
Making use of the solution of the foregoing problem, determine the probability of the particle with energy $E = U_{0} / 2$ to be located in the region $x > l$ , if $l^{2} U_{0} = {(\frac{3}{4} π)}^{2} \frac{ħ^{2}}{m}$ .View Solution
Question 39
Find the possible values of energy of a paraticle of mass $m$ located in s spheri View Solution
Question 40
From the condition of the foregoing problem find:
(a) normalized eigenfunctions of the particle in the states for which $Ψ (r)$ depends only on $r$ ,
(b) the most probable value $r_{p r}$ for the ground state of the particle and probability of the particle to be in in the region $r < r_{p r}$ View Solution
Question 41
A particle of mass $m$ is located in a spherically symmetrical potential well $U (r) = 0$ for $r < r_{0}$ and $U (r) = U_{0}$ for $r > r_{0}$ .
(a) By means of the substitution $Ψ (r) = ξ (r) / r$ find the equation defining the proper values of energy $E$ of the particle for $E < U_{0}$ , when its motion is described by a wave function $Ψ (r)$ depending only on $r$ . Reduce that equation to the form
$sin k r_{0} \pm k r_{0} \sqrt{ħ^{2} / 2 m r_{0}^{2} U_{0}}, w h e r e k = \sqrt{2 m E /} ħ$
(b) Calculate the value of the quantity $r_{0}^{2} U_{0}$ at which the first level appears.View Solution
Question 42
The wavefunction of a particle of mass $m$ in a unidimensional potential field $U (x) = k x^{2} / 2$ has in the ground state the form $Ψ (x) = A e^{- α x^{2}}$ , where $A$ is a normalization factor and $α$ is positive constant. Making use of a Schrodinger equation, find the constant $α$ and the energy $E$ of the particle in this state.View Solution
Question 43
Find the energy of an electron fo a hydrogen atom in a stationary state for which the wave function takes the from $Ψ (r) = A (1 + a r) e^{- α r}$ , where $A, a and α$ are constant.View Solution
Question 44
The wave fucnction of an electron of a hydrogen atom in the ground state takes the from $Ψ (r) = A e_{1}^{- r / r_{1}}$ , where $A$ is a certain constant, $r_{1}$ is the first Bohr radius. Find:
(a) the most probable distance between the electron and the nucleus.
(b) the mean value of modulus of the Coulomb force acting on the electron
(c )the mean value of the potential energy of the electron in the field of the nucleus.View Solution
Question 45
Find the mean electrostatic potential produced by an electron in the centre of a hydrogen atom if the electron is in the ground state for which the wave function is $Ψ (r) = A e_{1}^{- r / r_{1}}$ , where $A$ is a certain constant, $r_{1}$ is the first Bohr radius.View Solution
Question 46
Particle of mass $m$ and energy $E$ moves from the left to the potential barrier shown in figure. Find:
(a) the reflection coefficient $R$ of the barrier for $E > U_{0}$
(b) the effective penetration depth of the particles into the region $x > 0$ for $E < U_{0}$ i.e., the distacne from the barrier boundary to the point at which the probability of finding a particle decreases e-fold
View Solution
Question 47
Employing Eq.(6.2e), find the probability $D$ of an electron with energy $E$ tunneling through a potential barrier of width $l$ and height $U_{0}$ provided the barrier is shaped as shown:
(a) In fig 6.4
(b) in figure 6.5.

View Solution
Question 48
Using Eq.(6.2e), find the probability $D$ of a particle of mass $m$ and energy $E$ tunneling through the potential barrier shown in fig. where $U (x) = U_{0} (1 - x^{2} / l^{2})$ .View Solution

All Exercises from IE IRODOV PHYSICS Class 12 PHYSICS ATOMIC AND NUCLEAR PHYSICS

Home
Ask Doubt
Profile