A particle of mass mis located in a spherically symmetrical potential well U(r)=0 for r<r0 and U(r)=U0 for r>r0.
(a) By means of the substitution Ψ(r)=ξ(r)/r find the equation defining the proper values of energy E of the particle for E<U0, when its motion is described by a wave function Ψ(r) depending only on r. Reduce that equation to the form
sinkr0±kr0√ħ2/2mr20U0,wherek=√2mE/ħ
(b) Calculate the value of the quantity r20U0 at which the first level appears.
If we put Ψ=χ(r)r
the equation for χ(r) has the from
χ''k2χ=0,0≤r<r0
and χ''−α2χ=0r0<r<∞
where k2=2mEħ2,α2=2m(U0−E)ħ2
The boundary condition is
χ(0)=0andχχ'arecontinuousatr=r0}
These are exactly same as in the one dimensional problem in problem (6.85) We therefore omit further details.
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Molecules And Crystals
48 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Elementary Particles
20 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View Solution
Knowledge Check
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A B
B C
C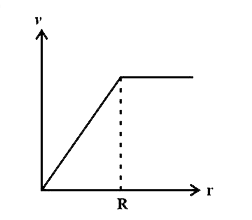 D
D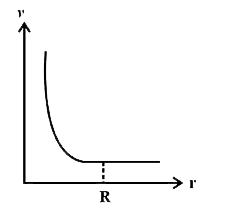
Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
Aρ0r24ε0RBρ0r4ε0RCρ0r4ε0RDρ0r2ε0RA spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A B
B C
C D
D
The potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View SolutionThe mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
View SolutionA particle with kinetic energy T is deflected by a spherical potential well radius R and depth U0 i.e., by the field in which the potential energy of the particle takes the form
U={0 for r>R−U0 for r<R
where r is the distance from the centre of the well. Find the relationship between the aiming parameter b of the particle and the angle θ through which it deflects from initial motion direction.
View SolutionThe mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View Solution
