Using the Schrodinger equation, demonstrate that at the point where the potential energy U(x) of a particle has a infinte discountinuity, the wave function renains smooth, I.e., its first derivaltive with respect to the coordinate is continuous.
We can for definiteness assume that the discontinuity occurs at the point x=0. Now the schordinger equation is
ħ22md2Ψdx2+U(x)Ψ(x)=EΨ(x)
We intergate this equation around x=0i.e., from x=−ε1→x=ε2 where ε1,ε2 are small positives numbers. Then
ħ22m∫+ε2−ε1d2Ψdx2dx=∫+ε2−ε1(E−U(x)Ψ(x)dx) ltbrltgt or (dΨdx)+ε2=(dΨdx)−ε1=−2mħ2∫ε2−ε1(E−U(x))dxΨ(x)
SInce the potential and the energy E are finite and Ψ(x) is bounded by assumption, the intergaral on the right exists and →0asε1,ε2→0
Thus (dΨdx)ε2=(dΨdx)−e1asε1,ε2→0
So (dΨdx) is continuous at x=0 (the point where U(x) has a infinite jump discontuinuityI (dΨdx)ε2=(dΨdx)−e1asε1,ε2→0
So (dΨdx) is continuous at x=0 (the point where U(x) has a infinite jump discontuinuity.
Topper's Solved these Questions
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Properties Of Atom
69 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Molecules And Crystals
48 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Elementary Particles
20 Videos
- DIRECT CURRENTBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - DIRECT CURRENTEXERCISE - All Questions
15 Videos
Similar Questions
Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View Solution
Knowledge Check
A particle with total energy E moves in one dimemsional region where the potential energy is U(x) The speed of the particle is zero where
AU(x)=0BU(x)=ECdU(x)dx=0Dd2U(x)dx2=0Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-Aa2y+bx2=0Ba2y=bx2Cy=ba2Day2=b2xA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
Aoscillatory motion but not simple harmonic motion about its mean position for small displacementsBsimple harmonic motion with time period 2π√8a2mb4 about its mean position for small displacementsCneither simple harmonic motion nor oscillatory about its mean position for small displacementsDnone of the above
A particles is in a unidirectional potential field where the potential energy (U) of a partivle depends on the x-coordinate given by Ux=k(1−cosax) & and 'a' are constant. Find the physical dimensions of 'a' & k.
View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
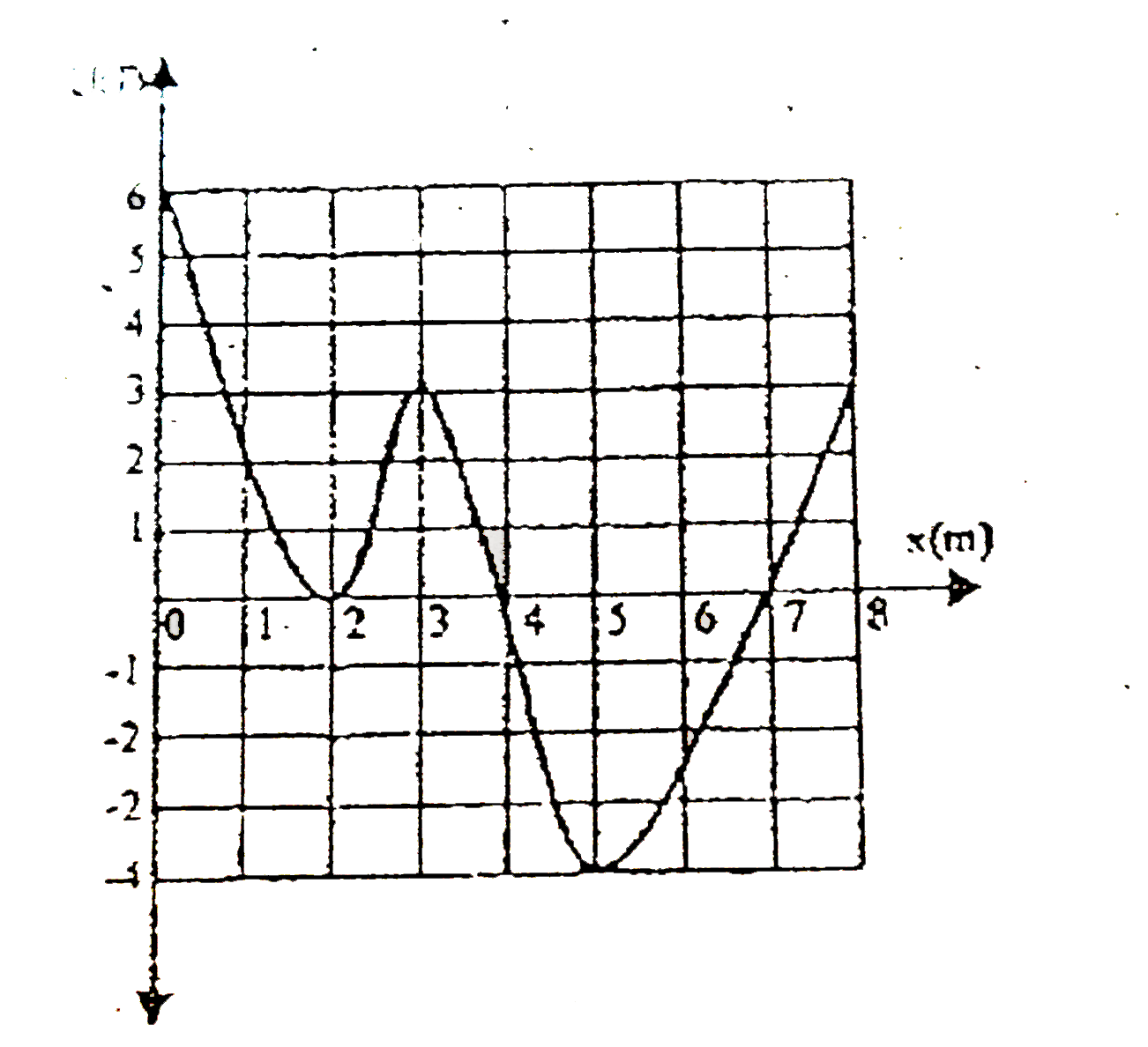
View SolutionPath traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
In above question initial acceleration (i.e.d2→rdt2) of particle is, if r =at i ^ −bt 2 j ^:-
View SolutionA single conservative force F(x) acts on a particle that moves along the x - axis. The graph of the potential energy with x is given. At x=5m, the particle has a kinetic energy of 50 J and its potential energy is related to position 'x' as U=15+(x−3)2 Joule where x is in meter. Then:
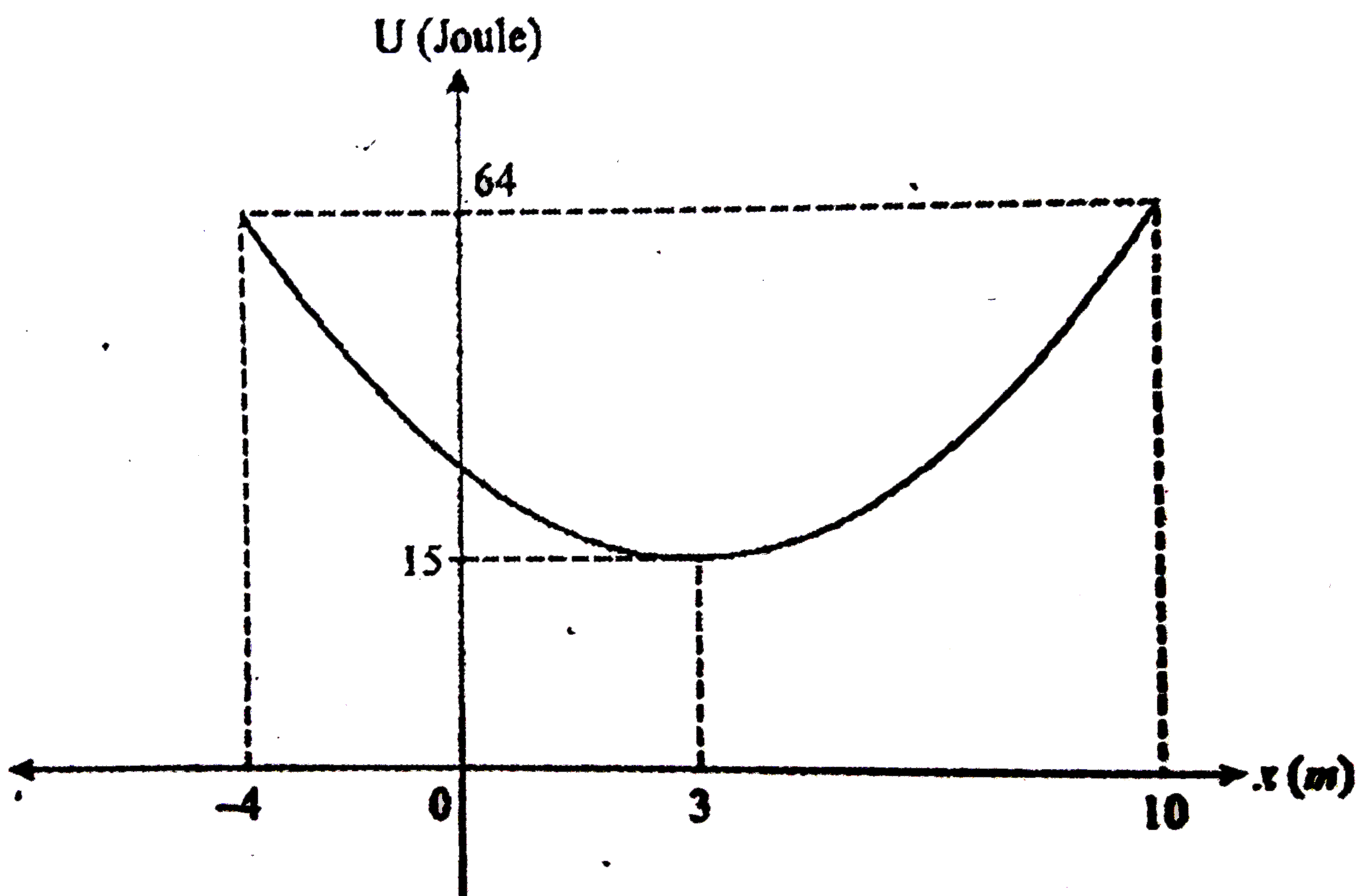
View SolutionPotential energy curve U of a particle as function of the position of a particle is shown. The particle has total mechanical energy E of 3.0 joules. Then select correct alternative.
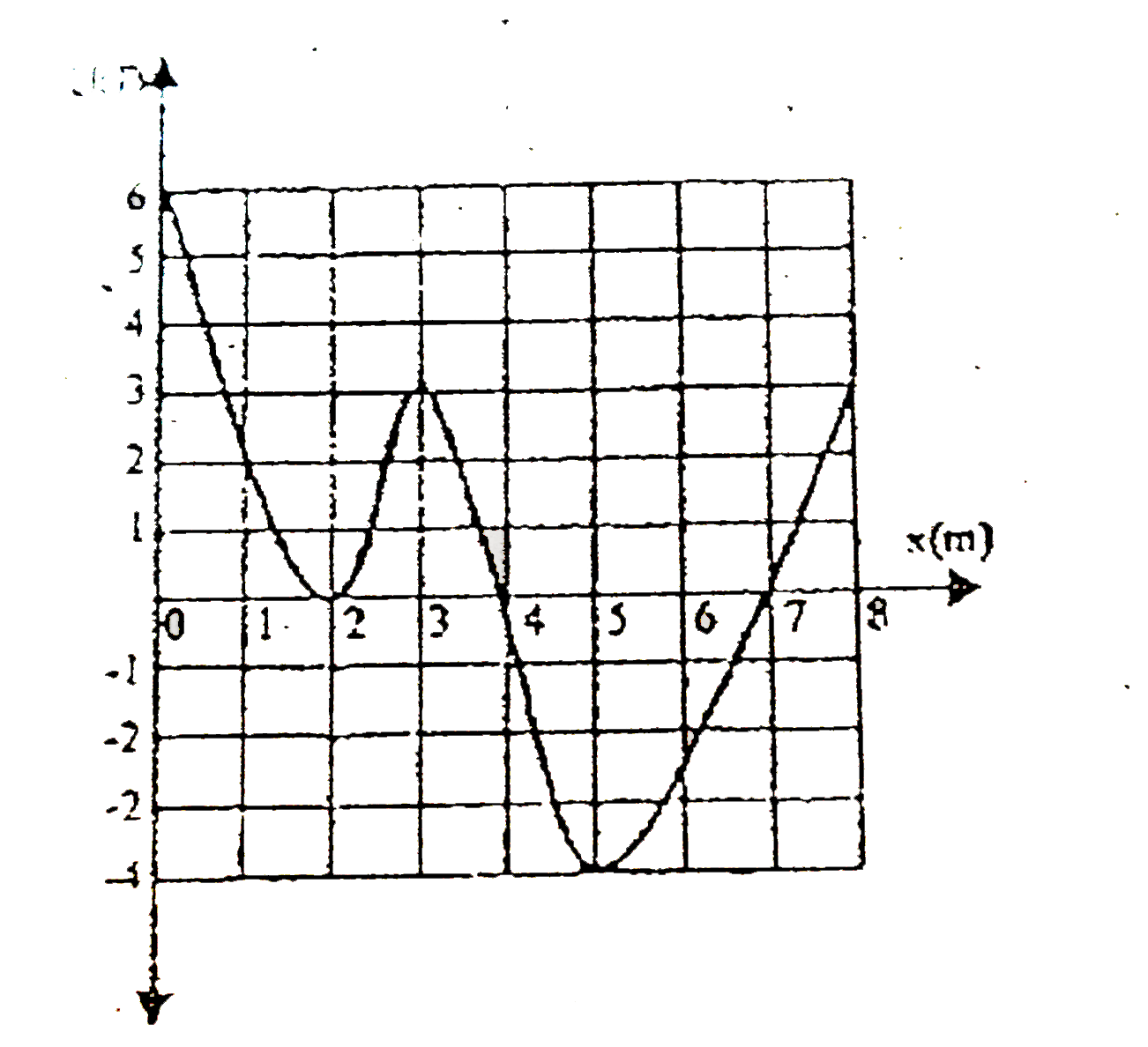
View Solution
