In Fig. 12.47 a sector OAP of a circle with centre O containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r[tanθ+secθ+πθ/180º-1]
Solution is..........
Related Solutions
In Fig. 4, a sector OAP of a circle with centre O, containing . AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is r.
[tan 0 + sec 0 +
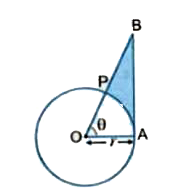
View SolutionIn the given figure, is shown a sector OAP of a circle with centre 0, containing . AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is
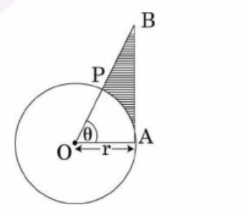
View SolutionIn the given figure,is shown a sector OAP of a circle with centre 0, containing /_ theta. AB is perpendicular to the radius OA and meets OP produced at B.Prove that the perimeter of shaded region is r[tan theta+sec theta+pi(theta)/(180)-1]
View Solutionis equal to
(a)secθ+tanθ
(b) secθ−tanθ
(c) sec 2 θ+ tan 2 θ
(d) sec 2 θ− tan 2 θ
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionFig. 15.17, shows a sector of a circle, centre , containing an angle , prove that: (FIGURE) (i) Perimeter of the shaded region is (ii) Area of the shaded region is
View SolutionFig. 15.17, shows a sector of a circle, centre , containing an angle , prove that: (FIGURE) (i) Perimeter of the shaded region is (ii) Area of the shaded region is
View SolutionIn Fig. 2.47, O is the centre of the circle.
Shade sectors OAC and OPB.
View Solution(1+tanθ+secθ)( 1+cotθ−cosec θ )= (a) 0 (b) 2 (c) 1 (d) −1
View Solution(1+tanθ+secθ)( 1+cotθ−cosec θ )= (a) 0 (b) 2 (c) 1 (d) −1
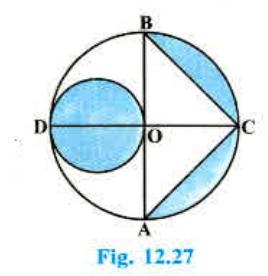
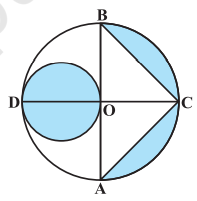
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
View SolutionThe number of distinct solutions of secθ+tanθ= √3 , 0≤θ≤3π , is
View SolutionIn the figure,AB is a diameter of the circle with centre O and OA=7cm. Find the area of the shaded region
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionFigure shows a sector of a circle, centre O, containing an angle . Prove that (i) Perimeter of the shaded region is (ii) Area of shaded region is
View Solutionदी आकृति में , AB और PQ एक वृत्त के लंबवत व्यास है जिसका केंद्र O और त्रिज्या OA = 7 सेमी है । छायांकित भाग का क्षेत्रफल ज्ञात कीजिए ।
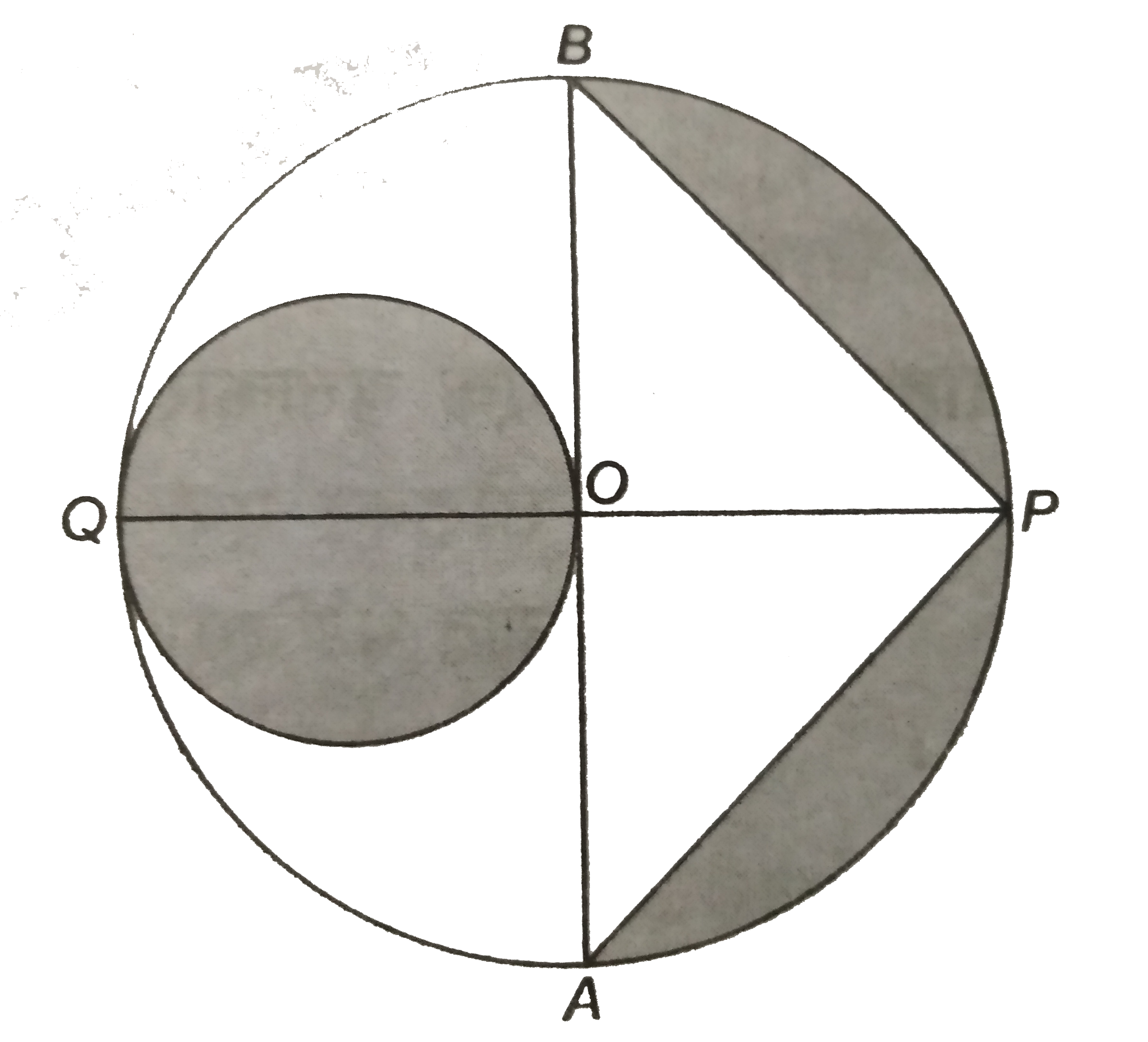
View SolutionIn Fig. 12.55, AB and CD are two perpendicular diameters of a circle with centre O. If OA= 7 cm, find the area of the shaded region. .
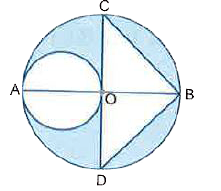
View SolutionIn Fig. 12.27, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If , find the area of the shaded region
View SolutionFigure shows a sector of a circle with centre O and angle . Prove that:
(a) Perimeter of shaded region is
(b) area of the shaded region is
View Solution