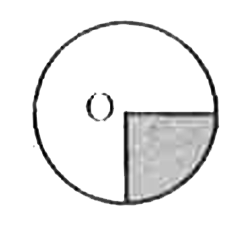
The M.I of a disc of mass M and radius R about an axis passing through the centre O and perpendicular to the plane of disc is MR2 / 2. If one quarter of the disc is removed the new moment of inertia of disc will be….. A MR2 / 3 B MR2 / 4 C 3/8 MR2 D 3/2 MR2
Correct option: C 3/8 MR2Explanation:MI of disc = [MR2 / 2]if one quarter disc is removed new mass = 3/4MRadius remains ∙ R2 / 2same hence new MI of disc = 3/4M = 3/8MR2
Related Solutions
The M.I. of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is . If one quarter of the disc is removed, the new moment of inertia of the disc will be
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionFrom a circular disc of radius R and mass 9m a small disc of radius (R/3) is removed from the disc the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is (
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View SolutionForm a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is
View SolutionFrom a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionA thin disc of mass 9 M and radius R from which a disc of radius R/3 is cut. Moment of inertia of the disc about an axis passing through O and perpendicular to plane of disc is
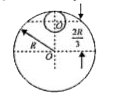
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionThe M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionA thin disc of mass 9 M and radius R from which a disc of radius R/3 is cut. Moment ofinertia,of the disc about an axis passing through O and perpendicular to plane of disc is
View SolutionThe moment of Inertia of a uniform semicircular disc of mass M and radius 'r' about a line perpendicular to the plane of the disc through the centre is :
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the centre is ………..
View SolutionA circular disc of mass M and radius R (R)/(3) A small disc is cut, the inertia of the remainder of the disc about an axis passing through the center O, perpendicular to the plane of the disc, is
View SolutionOne quarter of the disc of mass m is removed. If r be the radius of the disc, the new moment of inertia is
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
View Solution