Let ABCD be a convex quadrilateral. Let the diagonals AC and BD intersect in P. Let PE PF PG and PH be the altitudes from P on to the sides AB BC CD and DA respectively. Show that ABCD has an incircle if and only if 1/PE + 1/PG = 1/PF + 1/PH.
Let AP = p BP = q CP = r DP = s; AB = a BC = b CD = c and DA = d. Let ∠APB = ∠CPD = θ. Then ∠BPC = ∠DPA = π - θ. Let us also write PE = h1 PF = h2 PG = h3 and PH = h4.Observe thath1a = pqsinθ; h2b = qrsinθ; h3c = rssinθ; h4d = spsinθ.This is the same as ars + cpq = bsp + dqr.Thus we have to prove that a+c = b+d if and only if ars+cpq = bsp+dqr. Now we can write a + c = b + d as a2 + c2 + 2ac = b2 + d2 + 2bd. But we know that a2 = p2 + q2 - 2pqcosθ; c2 = r2 + s2 - 2rscosθb2 = q2 + r2 + 2qrcosθ; d2 = p2 + s2 + 2pscosθ; Hence a + c = b + d is equivalent to -pqcosθ + -rscosθ + ac = pscosθ + qrcosθ + bd. Similarly by squaring ars + cpq = bsp + dqr we can show that it is equivalent to -pqcosθ + -rscosθ + ac = pscosθ + qrcosθ + bd. We conclude that a + c = b + d is equivalent to cpq + ars = bps + dqr. Hence ABCD has an in circle if and only if1/h1 + 1/h3 = 1/h2 + 1/h4.
Related Solutions
ABCD is a quadrilateral whose diagonals AC and BD intersect at O, prove that: (AB+BC+CD+DA)>(AC+BD)
View SolutionABCD is a quadrilateral whose diagonals AC and BD intersect at O, prove that: (AB+BC+CD+DA)>2(AC+BD)
View Solutionदिखाइये कि एक चतुर्भुज ABCD में
View SolutionShow that in a quadrilateral ABCD
View SolutionIn a quadrilateral ABCD, show that
.View SolutionShow that in a quadrilateral ABCD
View SolutionIn a quadrilateral ABCD, show that
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View SolutionLet ABCD be a convex quadrilateral with perpendicular diagonals. If AB=20, BC=70 and CD=90, then what is the value of DA?
View Solutionमाना ABCD एक समलम्ब चतुर्भुज हो जहाँ AB |। CD और विकर्ण AC और BD के मध्य-बिन्दु क्रमशः P और Q हों, तब =
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a)
(b)
 View Solution
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a)
(b)
 View Solution
View SolutionLet ABC be an equilateral triangle and P be a point within the triangle.Perpendicular PD,PE and PF are drawn to three sides of the triangle,then the value of (AB+BC+CA)/(PD+PE+PF) is
View SolutionABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonal show that: PQ=SR
View SolutionABCD is a quadrilateral in which P,Q,R and S are the mid points of sides AB,BC,CD and DA respectively AC is a diagonal show that: PQRS is a parallelogram.
View SolutionBD, की समद्विभाजक है। BD पर स्थित एक बिन्दु P से AB और BC पर लम्ब क्रमशः PE और PF डाले गये है। सिद्ध कीजिए कि :
(i) (ii) PE=PF.View SolutionBD is the disector of angle ABC. From a point P in BD, perpendiculars PE and PF are drawn to AB and BC respectively, prove that :
(i) Triangle BEP is conguent to triangle BFP (ii) PE=PF.View SolutionBD is the disector of angle ABC. From a point P in BD, perpendiculars PE and PF are drawn to AB and BC respectively, prove that :
(i) Triangle BEP is conguent to triangle BFP (ii) PE=PF.View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
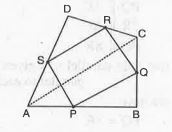 AC is a diagonal Show that .View Solution
AC is a diagonal Show that .View SolutionABCD is a quadrilateral in which P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively (See Fig.
 AC is a diagonal Show that .View Solution
AC is a diagonal Show that .View Solution
