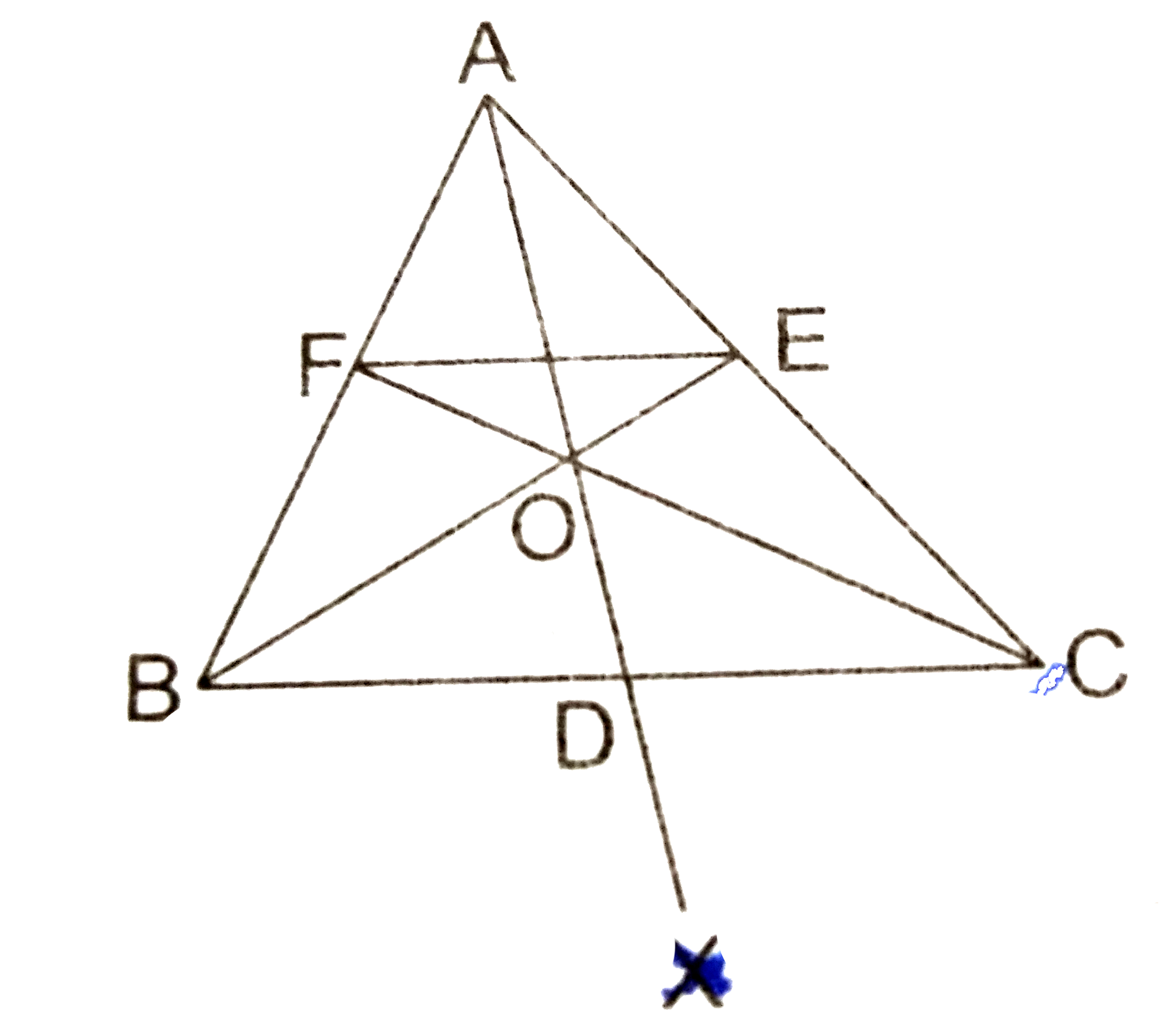
In the given figure side BC of a ∆ABC is bisected at D and O is any point on AD. BO and CO produced meet AC and AB at E and F respectively and AD is produced to X so that D is the midpoint of OX. Prove that AO : AX = AF : AB and show that EF║BC.
It is give that BC is bisected at D. ∴ BD = DC It is also given that OD =OX The diagonals OX and BC of quadrilateral BOCX bisect each other. Therefore BOCX is a parallelogram. ∴ BO || CX and BX || CO BX || CF and CX || BE BX || OF and CX || OE Applying Thales’ theorem in ∆ ABX we get:Applying the converse of Theorem in ∆ ABC EF || CB. This completes the proof.
Related Solutions
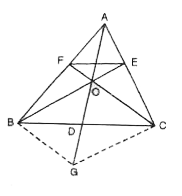
The side BC of a DeltaABC is bisected at D. O is any point on AD, BO and CO are produced to meet AC and AB at E and F respectively and AD is produced to G so that D is the midpoint of OG. Prove that FE|| BC
View SolutionIn the given figure, side BC of is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that and show that .
 View Solution
View Solutionएक त्रिभुज ABC की भुजा BC का मध्य बिंदु D है| मध्यिका AD पर O कोई बिंदु है| BO और CO को मिलते हुए इस प्रकार बढ़ाइए की ये AC और AB को क्रमशः E और F पर काटें|मध्यिका AD को X तक इस प्रकार बढाया गया है की बिंदु D ,OX का मध्य बिंदु है| सिद्ध करो की की
View SolutionThe side BC of a triangle ABC is bisected at D; O is any point in AD. BO and CO produced meet AC and AB in E and F respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO:AX=AF:AB and show that FE||BC.
View SolutionThe side of a triangle is bisected at is any point in produced meet in respectively and is produced to so that is the mid-point of Prove that and show that
View Solutionकी भुजा BC बिंदु D पर समद्विभाजित होती है AD पर कोई बिंदु O है बधाई गयी BO और CO क्रमसः AC और AB को E और F पर मिलती है तथा AD को X तक इस प्रकार बढ़ाया गया है कि D, AX का मध्य बिंदु है सिद्ध कीजिये कि AO : AX = AF : AB और दिखाईये कि FE || BC
View SolutionThe side BC of a DeltaABC is bisected at D. O is any point on AD. BO and CO are produced to meet AC and AB at E & F respectively. AD is produced to C1 so that D is the mid-point of OC1. Prove that FE||BC.
View Solutionबिन्दु D, E, F क्रमशः त्रिभुज की भुजाओ BC, CA और AB के मध्य-बिन्दु है। सिद्ध करे कि AD, EF को समद्विभाजित करता है।
View SolutionThe side of a triangle is bisected at is any point in produced meet in respectively and is produced to so that is the mid-point of . Prove that and show that .
View Solutionयदि की भुजाओं BC,CA और AB के मध्यबिंदु क्रमशः D,E और F हों तो सिद्ध कीजिए कि AD रेखाखंड EF को समद्विभाजित करती है।
View SolutionO is any point in the plane of the triangle ABC,AO,BO and CO meet the sides BC,CA nd AB in D,E,F respectively show that
View SolutionO is any point in the plane of the triangle ABC,AO,BO and CO meet the sides BC,CA nd AB in D,E,F respectively show that
View SolutionABC is a triangle and 'O', any point in the palne of the triangle. The lines AO, BO and CO meet the sides BC, CA and AB is D,E,F respectively. Then equal to
View SolutionIn F are mid-points of the sides BC, CA and AB respectively . Show that :
AD is perpendicular to EF.View Solutionमें, AD एक माध्यिका है । और के समद्विभाजक क्रमशः AB एवं AC से E एवं F बिन्दु पर मिलते है । सिद्ध कीजिए कि है ।
View SolutionIn F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.View SolutionThe side AC of a triangle ABC is produced to point E so that AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
View Solutionमाना कि ABC एक समद्विबाहु त्रिभुज हैं, जहाँ AB=AC तथा D,E तथा F क्रमशः BC,CA तथा AB के मध्य-बिंदु हैं, तो सिद्ध करें कि AD EF तथा EF ,AD को समद्विभाजित करती है।
View SolutionThe side AC of a triangle ABC is produced to point E so that AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that:
View Solutionएक की भुजा BC बिंदु D पर समद्विभाजित है। भुजा AD पर कोई बिंदु O है। रेखाखण्ड BO तथा CO को आगे बढ़ाने पर भुजा AC तथा AB पर क्रमशः बिंदु E तथा F पर मिलती है। भुजा AD को बिंदु G तक आगे बढ़ाया गया है जहाँ बिंदु D,OG के मध्य बिंदु है। सिद्ध कीजिए कि AO=AG=AF AB , तथा
 View Solution
View Solution
