A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
(a) at the mean position of the platform
(b) for an amplitude of gω2
(c) for an amplitude of g2ω2
(d) at the highest position of the platform
The correct Answer is:B
For block A to move in SHM.
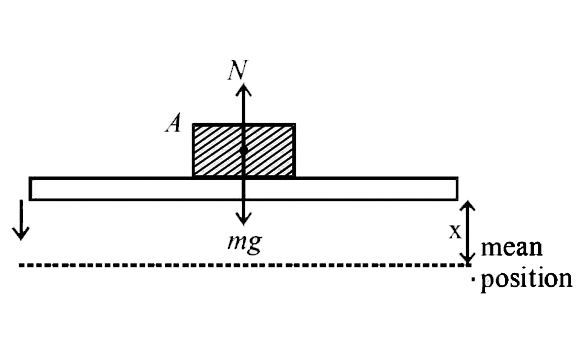
mg−N=mω2x
where x is the distance from mean position For block to leave contant N=0
⇒mg=mω2ξmpliesx=gω2
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
Similar Questions
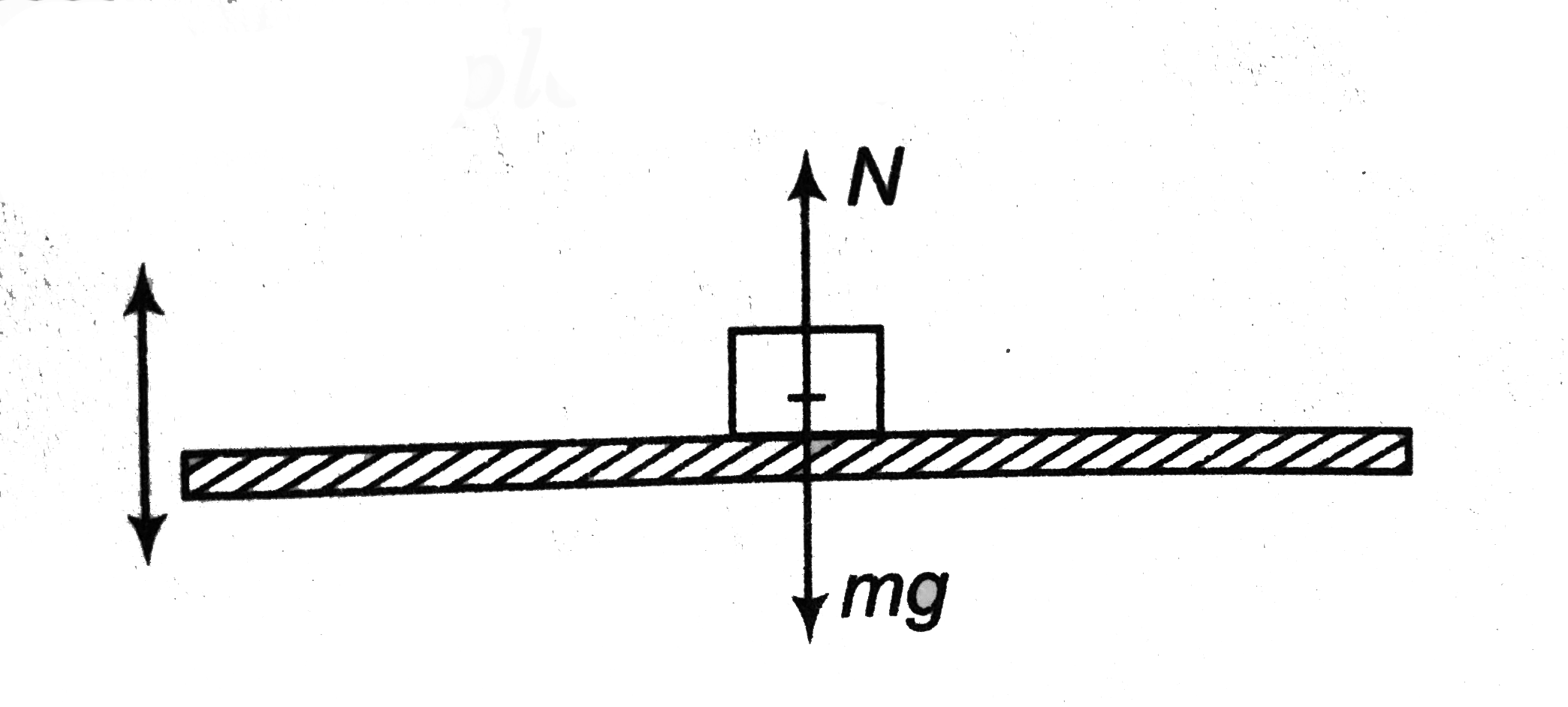
A block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
View SolutionA particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
View Solution
Knowledge Check
In the previous question, the angular frequency of the simple harmonic motion is ω. The coefficient of friction between the coin and the platform is μ. The amplitude of oscillation is gradually increased. The coin will begin to slip on the platform for the first time
(i) at the extreme positions of oscillations
(ii) at the mean position
(iii) for an amplitude of μgω2
(iv) for an amplitude of gμω2A(i),(iii)B(ii), (iii)C(i), (iv)D(ii),(iv)A coin is placed on a horizontal platform, which undergoes horizontal simple harmonic motion about a mean position O. The coin does not slip on the platform. The force of friction acting on the coin is F.
(i) F is always directed towards O
(ii) F is directed towards O when the coin is moving away from O, and away from O when the coin moves towards O
(iii) F=0 when the coin and platform come to rest momentarily at the extreme position of the harmonic motion
(iv) F is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motionAF is always directed towards OBF is directed towards O when the coin is moving away from O, and away from O when the coin moves towards OCF=0 when the coin and platform come to rest momentarily at the extreme position of the harmonic motionDF is maximum when the coin and platform come to rest momentarily at the extreme position of the harmonic motionThe total work done by the restoring force in simple harmonic motion of amplitude A and angular velocity ω in one oscillation is
A12mω2A2BmA2ω2CZeroD12mAω
A horizontal platform vibrate up and down with a simple harmonic motion of amplitude 20 c.m. At what frequency will an object kept on the platform remain just in contact with the platform ? Take g=9.81m/s2.
View SolutionThe total work done by a restoring force in simple harmonic motion of amplitude A and angular velocity. ω, in one oscillation is
View SolutionA particle undergoes simple harmonic motion having time period T. The time taken in 3/8th oscillation is
View SolutionA block of 0.5kg is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of 0.5Hz. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly
View SolutionA coin of mass m is placed on a horizontal platform which is undergoing S.H.M. about a mean position O in horizontal plane. The force of friction on the coin is f. while the coin does not slip on the platform f is
View Solution
