A highly rigid cubical block A of small mass and slide is fixed rigidly on to another cubical block B of the same dimensions and of low modulus of rigidity such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface. A small force is applied perpendicular to one of the sides faces of A. After the force is withdrawn, block A executes small oscillations the time period of which is given by.
(2 pi) sqrt (M eta)/(L)
The correct Answer is:D
To solve the problem, we need to determine the time period of the small oscillations of block A after a force F is applied and then withdrawn. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have two cubical blocks, A and B. Block A is rigid and has a small mass M, while block B has a low modulus of rigidity η. Block A completely covers block B, which is fixed to a horizontal surface.
Step 2: Apply the Force
A small force F is applied perpendicular to one of the side faces of block A. This force causes block B to deform slightly due to its low modulus of rigidity. The deformation leads to a shear strain in block B.
Step 3: Relate Force to Deformation
The shear stress (τ) in block B due to the applied force can be expressed as:
τ=FA
where A is the area of the face of block A in contact with block B, which is L2 (since the side length of the cube is L).
The shear strain (γ) is given by:
γ=ΔLL
where ΔL is the amount of deformation in block B.
Step 4: Use Modulus of Rigidity
The modulus of rigidity (η) relates shear stress and shear strain:
η=τγ
Substituting the expressions for shear stress and shear strain:
η=F/(L2)ΔL/L
Rearranging gives:
F=ηL2ΔL⋅ΔL=ηLΔL
Step 5: Relate to Simple Harmonic Motion
When the force F is removed, block A will oscillate about its equilibrium position. The restoring force can be modeled as:
F=−KΔL
where K is the effective spring constant. From our previous equation, we can identify:
K=ηLΔL
Step 6: Find Angular Frequency
In simple harmonic motion, the force can also be expressed as:
F=Mω2x
where x is the displacement from the equilibrium position. Setting the two expressions for force equal gives:
ηLΔL=Mω2ΔL
Cancelling ΔL (assuming it is not zero):
ηL=Mω2
Thus, we can solve for ω:
ω=√ηLM
Step 7: Calculate Time Period
The time period T of the oscillation is related to the angular frequency by:
T=2πω
Substituting for ω:
T=2π√MηL
Final Result
Thus, the time period of the oscillations of block A is given by:
T=2π√MηL
We have two cubical blocks, A and B. Block A is rigid and has a small mass M, while block B has a low modulus of rigidity η. Block A completely covers block B, which is fixed to a horizontal surface.
A small force F is applied perpendicular to one of the side faces of block A. This force causes block B to deform slightly due to its low modulus of rigidity. The deformation leads to a shear strain in block B.
The shear stress (τ) in block B due to the applied force can be expressed as:
τ=FA
where A is the area of the face of block A in contact with block B, which is L2 (since the side length of the cube is L).
γ=ΔLL
where ΔL is the amount of deformation in block B.
The modulus of rigidity (η) relates shear stress and shear strain:
η=τγ
Substituting the expressions for shear stress and shear strain:
η=F/(L2)ΔL/L
Rearranging gives:
F=ηL2ΔL⋅ΔL=ηLΔL
When the force F is removed, block A will oscillate about its equilibrium position. The restoring force can be modeled as:
F=−KΔL
where K is the effective spring constant. From our previous equation, we can identify:
K=ηLΔL
In simple harmonic motion, the force can also be expressed as:
F=Mω2x
where x is the displacement from the equilibrium position. Setting the two expressions for force equal gives:
ηLΔL=Mω2ΔL
Cancelling ΔL (assuming it is not zero):
ηL=Mω2
Thus, we can solve for ω:
ω=√ηLM
The time period T of the oscillation is related to the angular frequency by:
T=2πω
Substituting for ω:
T=2π√MηL
Thus, the time period of the oscillations of block A is given by:
T=2π√MηL
Topper's Solved these Questions
Similar Questions
A cubical block of side a and of mass m rests on a rough horizontal surface. A horizontal force F is applied to normal to one of the faces at height h above the base h>a/2. What is the minimum value of F for which the cube begins to tip about an edge?
View SolutionA force Fis tangentially applied on the upper face of a cube of side b and whose lower face is fixed. If modulus of rigidity is n then upper surface of cube is shifted to
View Solution
Knowledge Check
A highly rigid cubical block A of small mass M and side L is fixed rigidly on the other cubical block of same dimensions and of modulus of rigidity η such that the lower face of A completely covers the upper face of B. The lower face of B is rigidly held on a horizontal surface . A small force F is applied perpendicular to one of the side faces of A. After the force is withdrawn , block A executes faces of A. After the force is withdrawn , block A exceutes small oscillations , the time period of which is given by
A2π√MηLB2π√Mη/LC2π√ML/ηD2π√M/ηLthe gauge pressure at the lower face of the block is
A84PaB384PaC484PaD784PaOne of the square faces of a metal slab of side 50 cm and thickness 20 cm is rigidly fixed on a horizontal surface. If a tangential force of 30 N is applied to the top face and it is known that the shear modulus of the material is 4×1010N/m2, then the displacement (in m) of the top face is
A4×10−12mB4×10−10mC6×10−10mD8×10−10m
A cube with all six faces coloured is cut into 64 cubical blocks of the same size which are thoroughly mixed. Find the probability that the 2 randomly chosen blocks have 2 coloured faces each.
View SolutionA cubical block of side 10 cm floats at the interface of an oil and water. The pressure above that of atmosphere at the lower face of the block is
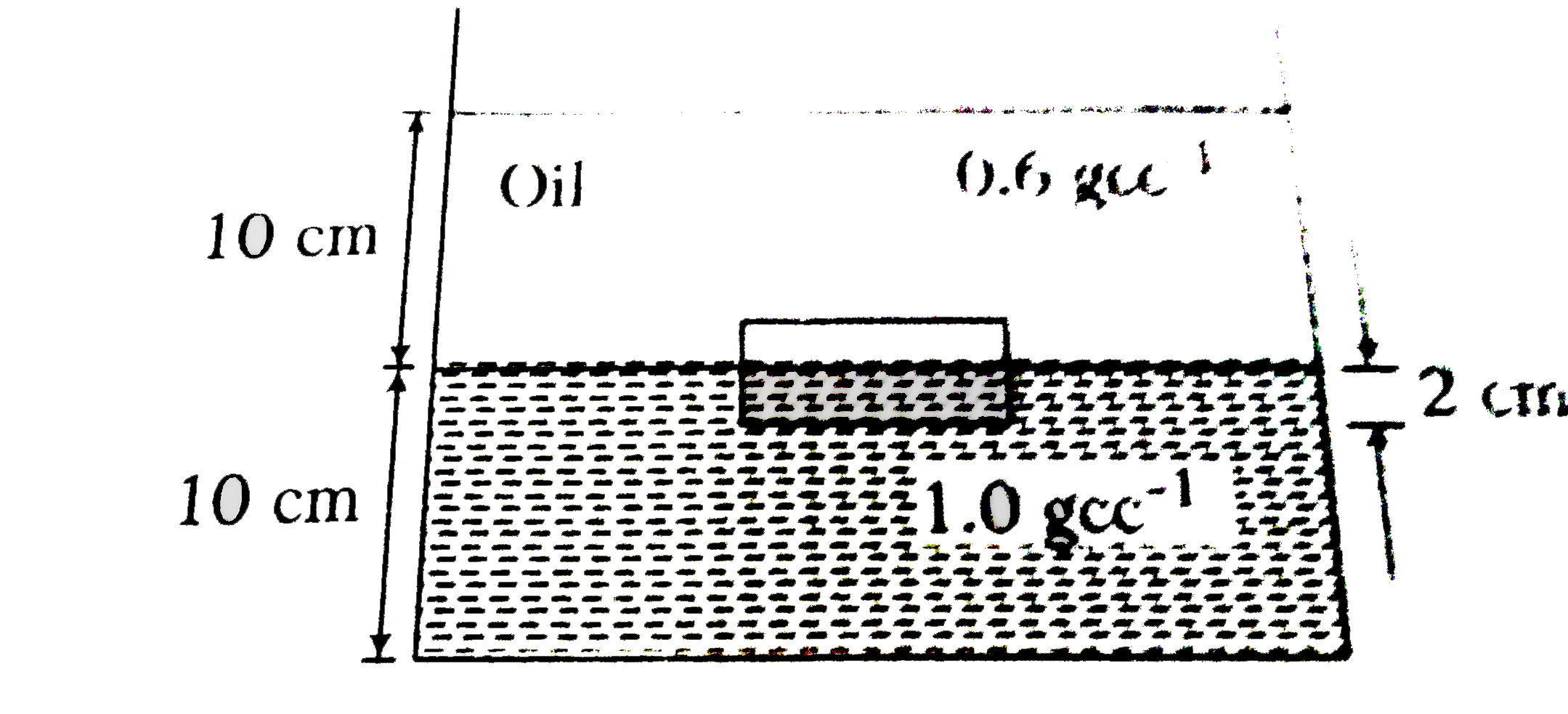
View SolutionTwo blocks of equal mass 2 kg are placed on a rough horizontally surfaces as shown and a force F is applied on the upper block . The system is initially at rest . Find acceleration of the lower block in m/s2 .

View SolutionA cubical block of side 10cm floats at the interface of an oil and water as shown in the figure. The density of oil is 0.6gcm−3 and the lower face of ice cube is 2cm below the interface. The pressure above that of the atomosphere at the lower face of the block is

View SolutionA block B of mass 0.6kg slides down the smooth face PR of a wedge A of mass 1.7kg which can move freely on a smooth horizontal surface.
The inclination of the face PR to the horizontal is 45∘ . Then :

View Solution
