Question

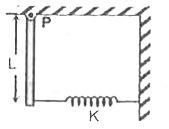
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :

Options

A. `2 pi (m //K)^(1//2)`
B. `2 pi sqrt(m ((Y A + KL)))/(YAK)`
C. `2 pi [(m Y A //K L)^(1//2)`
D. `2 pi [(m L // Y A)^(1//2)`

Answer

B

Explanation

To solve the problem of finding the time period (T) of the oscillation of a mass attached to a spring and a wire, we will follow these steps:

Step 1: Understand the System
We have a long metallic wire of length \(L\) tied to the ceiling, with a spring of spring constant \(K\) attached to the free end. A mass \(m\) is hanging from the spring. When the mass is pulled down and released, it will oscillate.

Step 2: Identify the Forces
When the mass is displaced, both the spring and the wire will experience tension. The total force acting on the mass when displaced by a distance \(x\) can be expressed as:
\( F = Kx + F_{\text{wire}} \)
where \(F_{\text{wire}}\) is the force due to the extension of the wire.

Step 3: Calculate the Extension of the Wire
The extension (\(\Delta L\)) of the wire can be calculated using Young's modulus (\(Y\)):
\( Y = \frac{F/A}{\Delta L/L} \)
Rearranging gives:
\( F = \frac{Y A \Delta L}{L} \)
Here, \(A\) is the cross-sectional area of the wire.

Step 4: Relate Forces to Spring Constant
The effective spring constant \(K'\) of the wire can be expressed as:
\( K' = \frac{Y A}{L} \)
Thus, the total effective spring constant \(K_{\text{eq}}\) of the system (spring and wire) when combined in series is:
\( \frac{1}{K_{\text{eq}}} = \frac{1}{K} + \frac{1}{K'} \)
Substituting \(K'\):
\( \frac{1}{K_{\text{eq}}} = \frac{1}{K} + \frac{L}{Y A} \)

Step 5: Calculate the Time Period
The time period \(T\) of a mass-spring system is given by:
\( T = 2\pi \sqrt{\frac{m}{K_{\text{eq}}}} \)
Substituting for \(K_{\text{eq}}\):
\( T = 2\pi \sqrt{\frac{m}{\left(\frac{1}{K} + \frac{L}{Y A}\right)^{-1}}} \)

Step 6: Simplify the Expression
After simplification, we can express \(T\) as:
\( T = 2\pi \sqrt{m \left(\frac{K Y A}{K Y + L}\right)} \)

Final Expression
Thus, the time period \(T\) of the oscillation is:
\( T = 2\pi \sqrt{\frac{m (K L + Y A)}{K Y A}} \)