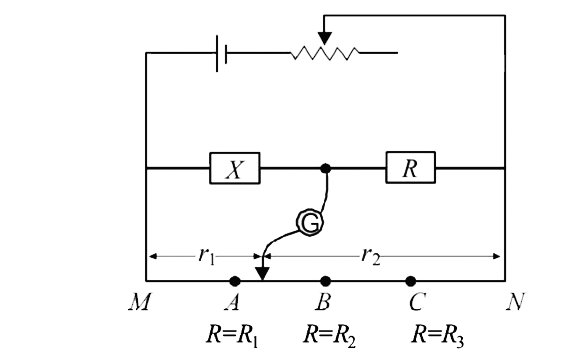
An unknown resistance X is to be determined using resistances R1,R2orR3. Their corresponding null points are A, B and C. Find which of the above will give the most accurate reading and why?
 . R=R1orR2orR3.
. R=R1orR2orR3.
The correct Answer is:B
KEY CONCEPT : At all null points the wheatstone bridge will
be balanced
∴Xr1=Rr2
⇒X=R(r1r2)
where R is a constant r1andr2 are variable.
The maximum fractional
error is
ΔXX=Δr1r1+Δr2r2
Here, Δr1=Δr2=y (say) then
For ΔXX→beminiμmr_1 xx r_2shod––bemax<br>[:. r_1 + r_2 = c (constt.)]<br>LetE = r_1 xx r_2<br>rArr E = r_1 xx (r_1-c)<br>:. (dE)/(dr_1) = (r_1-c) + r_1 = 0<br>rArr r_1 = c/2 rArr r_2 = c/2 rArr r_1 = r_2<br>rArr R_2 gives the most accureate value.
 .
.
Topper's Solved these Questions
Similar Questions
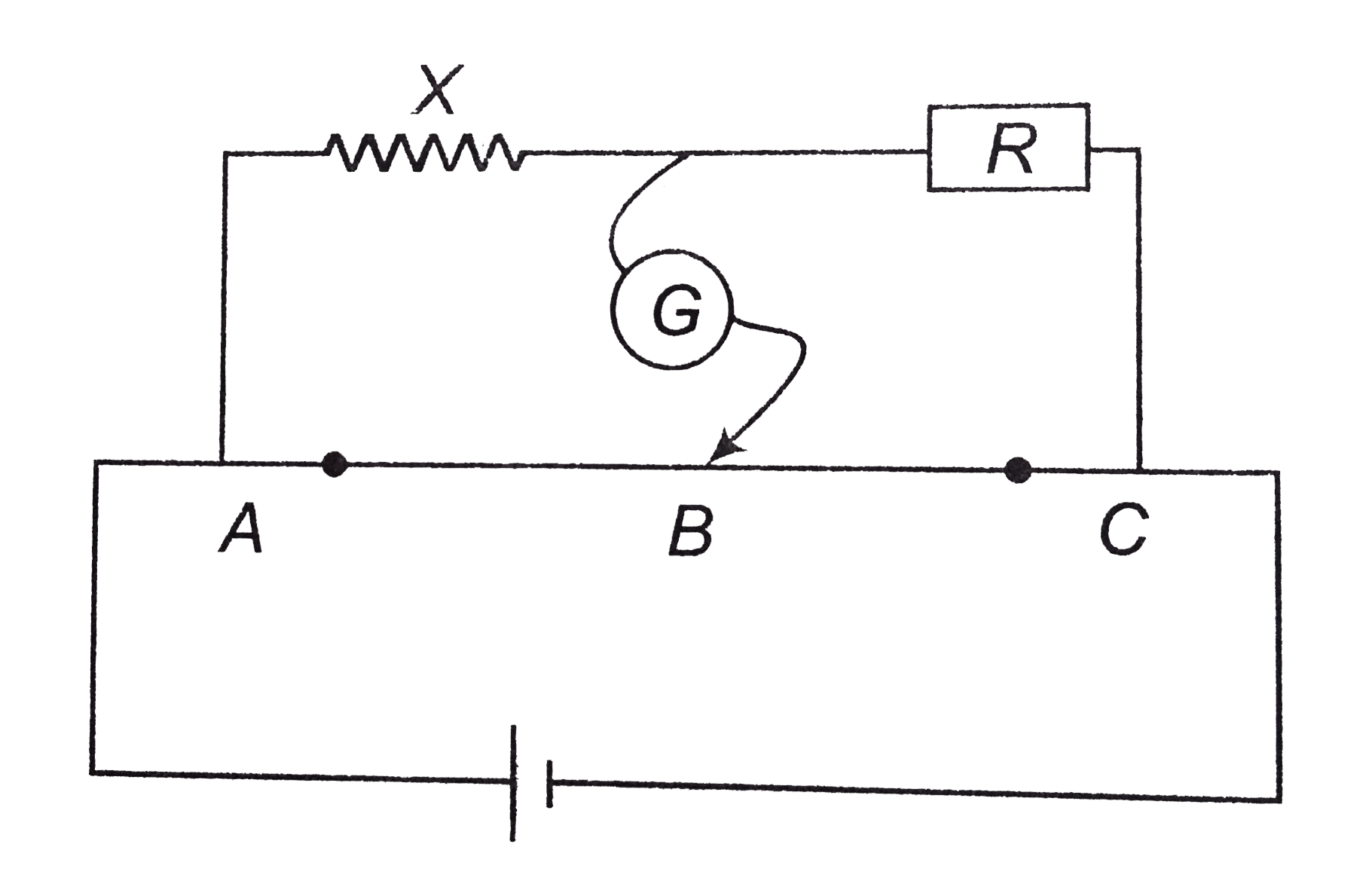
R1,R2,R3 are different values of R,A,B and C are the null points obtained corresponding to R1,R2 and R3 respectively. For which resistor, the value of X will be the most accurate and why?
View SolutionAn unknown resistance r is determined in terms of a standard resistance R=100 Ω by using potentiometer. The potential difference across r is balanced against 45 cm length of the wire and that (r+R) is obtained at 70 cm of the wire . Find the value of the unknown resistance in Ω.
View Solution
Knowledge Check
An unknown resistance r si determined in terms of a standared resistance R=100Ω by using potentiometer. The potential difference across r is balanced againt 45cm length of the wire and that (r+R) is obtained at 70cm of the wire. Find the value of the unknown resistance.
A200ΩB280ΩC180ΩD100Ωr1+r2+r3−r=
ARB2RC3RD4RTwo ideal batteries of emf V1andV2 and three resistances R1,R2andR3 are connected as shown in the figure. The current in resistance R2 would be zero if
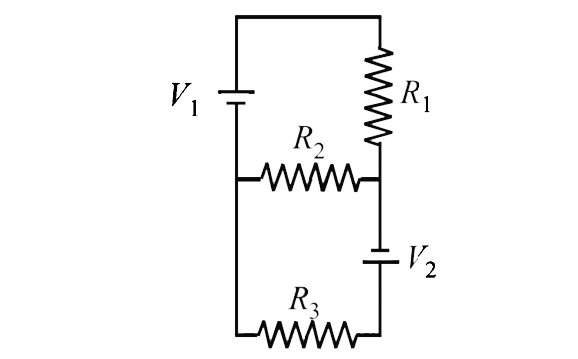 AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and3R1=R2=R3
AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and3R1=R2=R3
R1,R2,R3 are different values R,A,B and C are the null points obtained corresponding to R1,R2andR3 respectively. For which resistor, the value of X will be the most accurate and why?
 .
.
View SolutionIn the situation shown, resistance R1,R2 and R3 are in the ratio 3:2:1 , then
View SolutionShow that if three slabs of thermal resistance R1,R2 and R3 are placed in contact, the thermal resistance of the compound slab is given by R=R1+R2+R3.
View SolutionResistance R1and R2, each 60Ω, are connected in series. The points A and B is 120V. Find the reading of voltmeter connected resistance r=120Ω
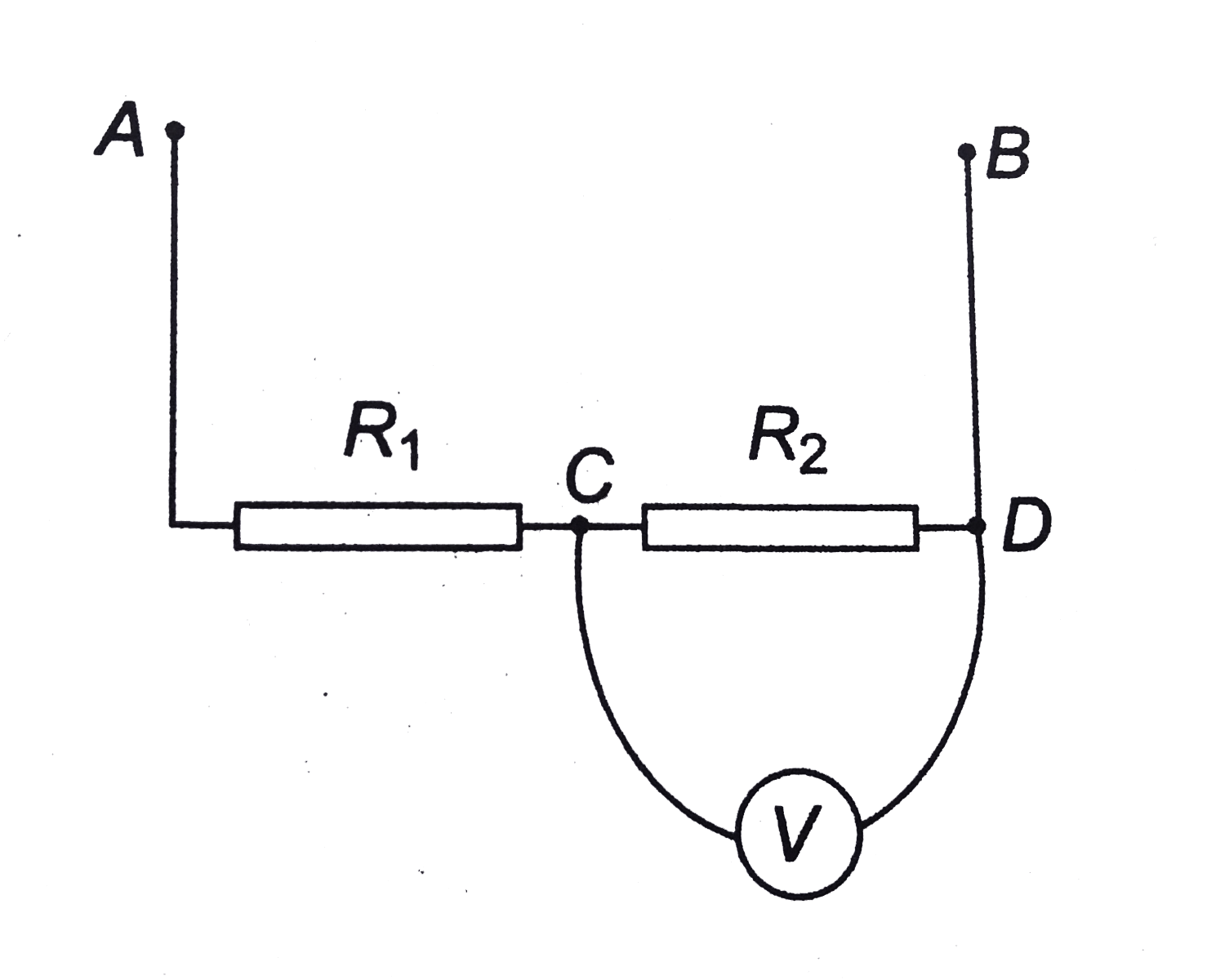
View SolutionWhen two resistors of resistances R1andR2 are connected in parallel, the net resistance is 3Ω. When connected in series, its value is 16Ω. Calculate the values of R1andR2.
View Solution