When two identical batteries of internal resistance each are connected in series across a resistor R, the rate of heat produced in R is . When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2Omega is
The correct Answer is:D
To solve the problem, we need to find the value of the resistor R when two identical batteries of internal resistance 1Ω each are connected in series and parallel across the resistor R. We are given that the rate of heat produced in R when the batteries are in series is J1 and when they are in parallel is J2, with the relation J1=2.25J2.
1. Determine the Current in Series Connection:
- When the two batteries are connected in series, the total voltage VT is 2V (where V is the voltage of each battery).
- The total internal resistance in series is 2Ω (since each battery has 1Ω).
- The total resistance in the circuit is R+2.
- The current I1 through the resistor R can be calculated using Ohm's law:
I1=VTR+2=2VR+2
2. Calculate the Power (Heat) in Series:
- The power J1 (rate of heat produced in R) is given by:
J1=I21R=(2VR+2)2R
- Simplifying this gives:
J1=4V2R(R+2)2
3. Determine the Current in Parallel Connection:
- When the two batteries are connected in parallel, the total voltage across R remains V (the same as one battery).
- The equivalent internal resistance Req of the two batteries in parallel is:
Req=111+11=12Ω
- The total resistance in this case is R+0.5.
- The current I2 through the resistor R can be calculated as:
I2=VR+0.5
4. Calculate the Power (Heat) in Parallel:
- The power J2 (rate of heat produced in R) is given by:
J2=I22R=(VR+0.5)2R
- Simplifying this gives:
J2=V2R(R+0.5)2
5. Relate J1 and J2:
- We know from the problem statement that:
J1=2.25J2
- Substituting the expressions for J1 and J2:
4V2R(R+2)2=2.25⋅V2R(R+0.5)2
- Canceling V2R from both sides (assuming V≠0 and R≠0):
4(R+2)2=2.25⋅1(R+0.5)2
6. Cross-Multiply and Simplify:
- Cross-multiplying gives:
4(R+0.5)2=2.25(R+2)2
- Expanding both sides:
4(R2+R+0.25)=2.25(R2+4R+4)
4R2+4R+1=2.25R2+9R+9
- Rearranging gives:
(4−2.25)R2+(4−9)R+(1−9)=0
1.75R2−5R−8=0
7. Solve the Quadratic Equation:
- Using the quadratic formula R=−b±√b2−4ac2a:
R=5±√(−5)2−4⋅1.75⋅(−8)2⋅1.75
R=5±√25+563.5
R=5±√813.5
R=5±93.5
- This gives two possible solutions:
R=143.5=4(valid)
R=−43.5(not valid)
Final Answer:
Thus, the value of R is 4Ω.
- When the two batteries are connected in series, the total voltage VT is 2V (where V is the voltage of each battery).
- The total internal resistance in series is 2Ω (since each battery has 1Ω).
- The total resistance in the circuit is R+2.
- The current I1 through the resistor R can be calculated using Ohm's law:
I1=VTR+2=2VR+2
- The power J1 (rate of heat produced in R) is given by:
J1=I21R=(2VR+2)2R
- Simplifying this gives:
J1=4V2R(R+2)2
- When the two batteries are connected in parallel, the total voltage across R remains V (the same as one battery).
- The equivalent internal resistance Req of the two batteries in parallel is:
Req=111+11=12Ω
- The total resistance in this case is R+0.5.
- The current I2 through the resistor R can be calculated as:
I2=VR+0.5
- The power J2 (rate of heat produced in R) is given by:
J2=I22R=(VR+0.5)2R
- Simplifying this gives:
J2=V2R(R+0.5)2
- We know from the problem statement that:
J1=2.25J2
- Substituting the expressions for J1 and J2:
4V2R(R+2)2=2.25⋅V2R(R+0.5)2
- Canceling V2R from both sides (assuming V≠0 and R≠0):
4(R+2)2=2.25⋅1(R+0.5)2
- Cross-multiplying gives:
4(R+0.5)2=2.25(R+2)2
- Expanding both sides:
4(R2+R+0.25)=2.25(R2+4R+4)
4R2+4R+1=2.25R2+9R+9
- Rearranging gives:
(4−2.25)R2+(4−9)R+(1−9)=0
1.75R2−5R−8=0
- Using the quadratic formula R=−b±√b2−4ac2a:
R=5±√(−5)2−4⋅1.75⋅(−8)2⋅1.75
R=5±√25+563.5
R=5±√813.5
R=5±93.5
- This gives two possible solutions:
R=143.5=4(valid)
R=−43.5(not valid)
Thus, the value of R is 4Ω.
Topper's Solved these Questions
Similar Questions
When two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View Solution
Knowledge Check
Two identical batteries, each of EMF 2V and internal resistance r=1Ω are connected as shown. the maximum power that can be developed across R using these batteries is :
 A3.2WB8.2WC2WD4W
A3.2WB8.2WC2WD4WTwo identical batteries, each of emf 2V and internal resistance r=1Ω are connected as shown. The maximum power that can be developed across R using these batteries is
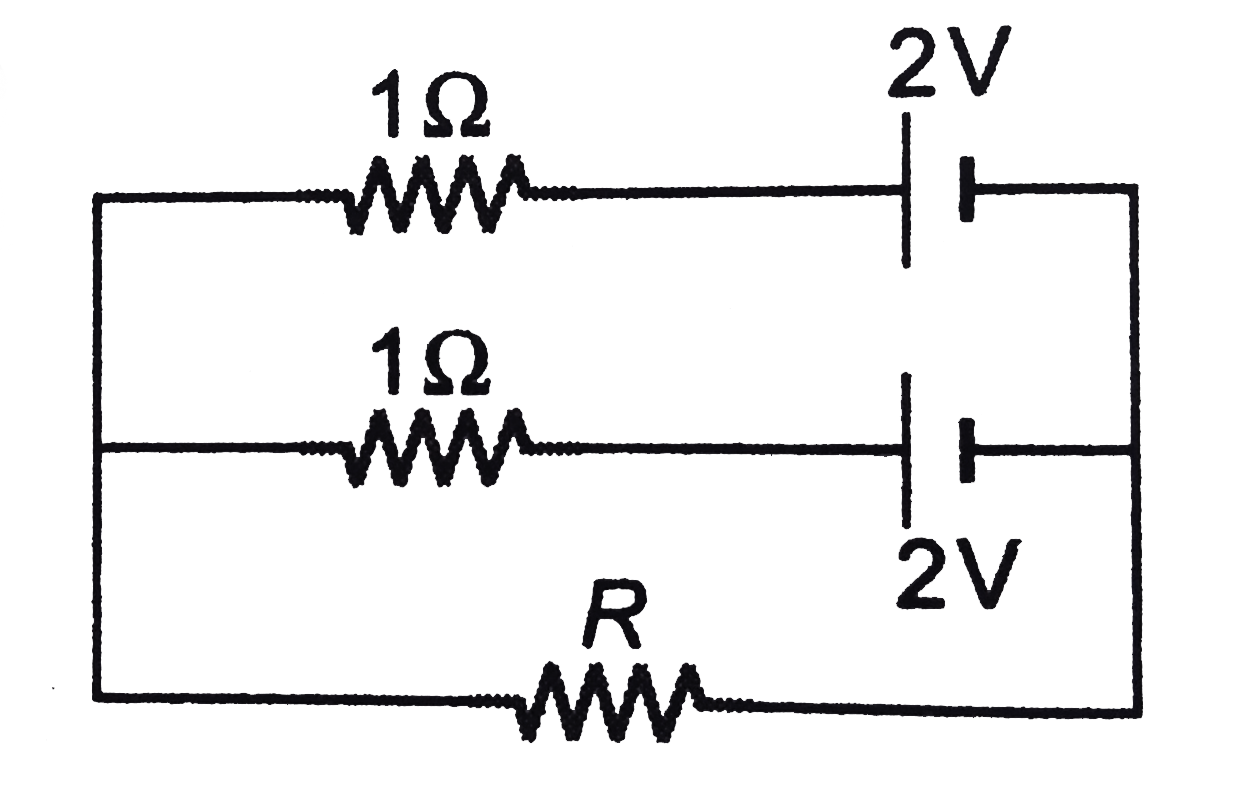 A3.2WB8.2WC2WD4W
A3.2WB8.2WC2WD4Wn identical calls, each of internal resistance (r) are first connected in parallel and then connected in series across a resistance (R). If the current through R is the same in both cases, then
AR=r2Br=R2CR=rDr=0
A galvanometer, together with an unknown resistance in series, is connected across two identical batteries of each 1.5V. When the batteries are connected in series,the galvanometer records a current of 1A, and when the batteries are connected in parallel, the current is 0.6A. In this case, the internal resistance of the battery is 1/'∗'Ω.
What is the value of '**'?
View SolutionFive identical cells each of internal resistance 1Ω and emf 5V are connected in series and in parallel with an external resistance 'R' . For what value of 'R', current in series and parallel combination will remain the same ?
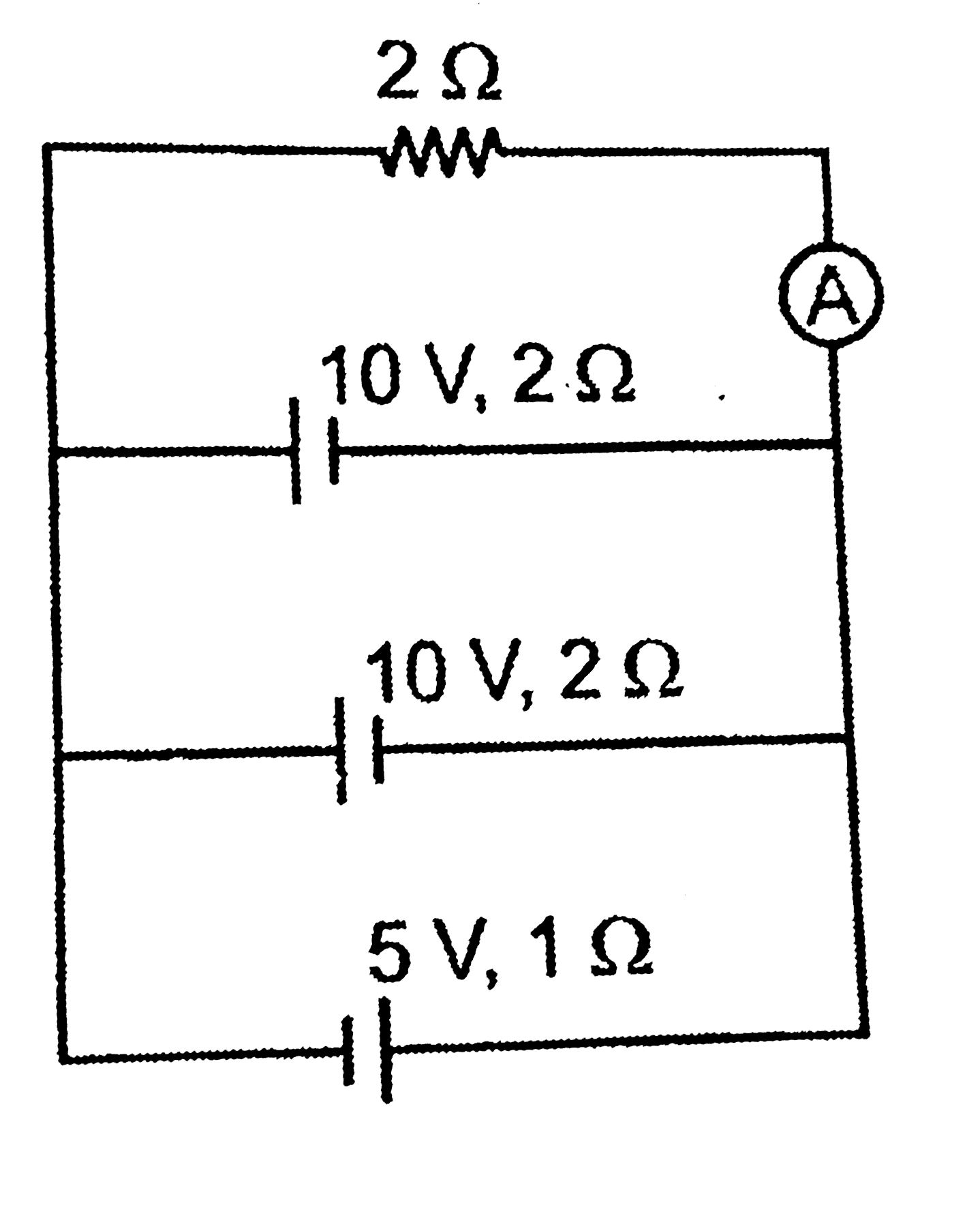
View SolutionThree batteries having emfs and internal resistances as shown in figure are connected across a resistor of 2Ω. The reading of ammeter is
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionTwo coils of resistances 3Ωand6Ω are connected in series across a battery of emf12V. Find the electrical energy consumed in 1 minute in each resistance when these are connected in series.
View Solution
