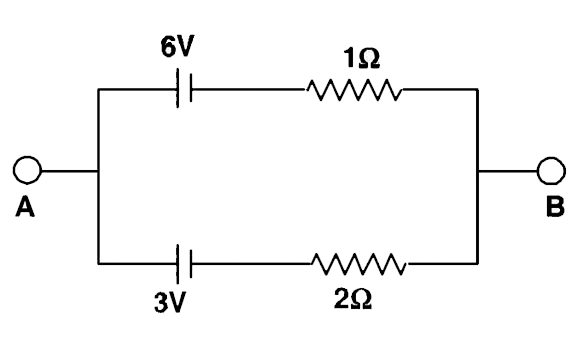
Two batteries of different emfs and different internal resistances are connected as shown. The voltage across AB in volts is.
 .
.
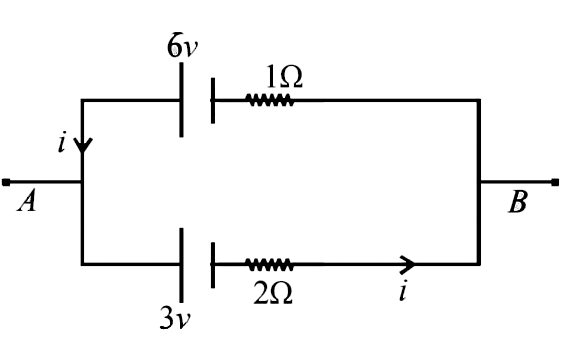
let i be the current flowing in the circuit. Apply Kirchhoff's
law in the loop we get
−3−2i−i+6=0
∴3i=3
∴i=1Amp.
Now let us travel in the circuit from A to B through battery of 6V, we get
VA−6+1×1=VB
:. V_(A) - V_(B) = 5 volt.
Topper's Solved these Questions
Similar Questions
The series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
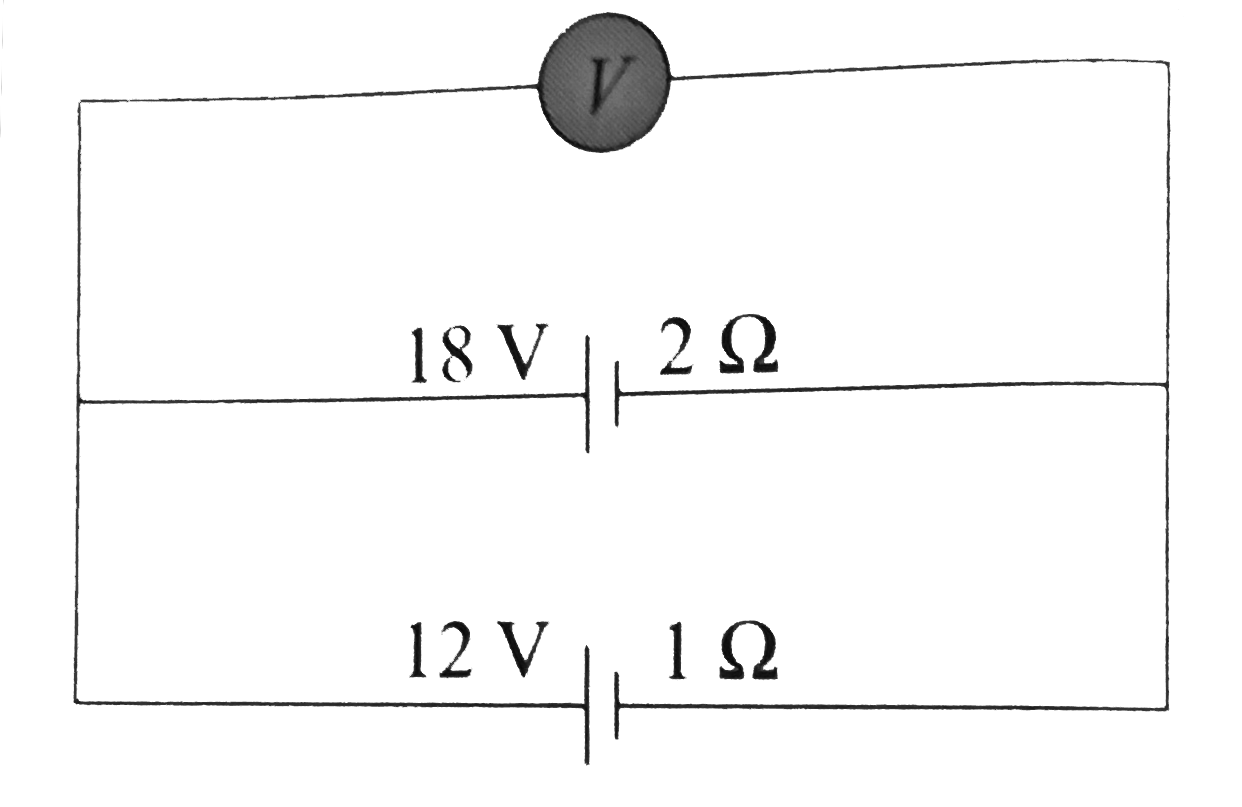
View SolutionTwo batteries, one of emf 18 volts and internal resistance 2Ω and the other fo emf 12 volts and internal resistance 1Ω, are connected as shown. The voltmeter V will record a reading of
View Solution
Knowledge Check
Two batteries of difference emf's and internal resistance are connected in parallel to one another.
AEquivalent emf will be grater than either of the emf'sBEquivalent emf will be smaller than either of the emfCEquivalent internal resistance will be grater than either of the two internal resistancesDEquivalent internal resistance will be smaller than either of the two internal resistances.Two batteries of different emf and internal resistances connected in series with each other and with an external load resistor. The current reversed, the current becomes 1.0 A. the ratio of the emf of the two batteries is
A2.5:1B2:1C3:2D1:1Two identical batteries, each having emf of 1.8 V and of equal internal resistances are connected as shown in the figure. Potential difference between A and B will be equal to (Ignore the resistance of lead wires)
 A3.6 VB1.8 VCzeroDNone of these
A3.6 VB1.8 VCzeroDNone of these
Two batteries, one of emf 18V and internal resistance 2Ω and the other of emf 12 and internal resistance 1Ω , are connected as shown. The voltmeter V will record a reading of

View SolutionTwo batteries of emf 4 V and 8 V with internal resistances 1Ω and 2Ω are connected in a circuit with a resistance of 9Ω as shown in figure. The current and potential difference between the points P and Q are
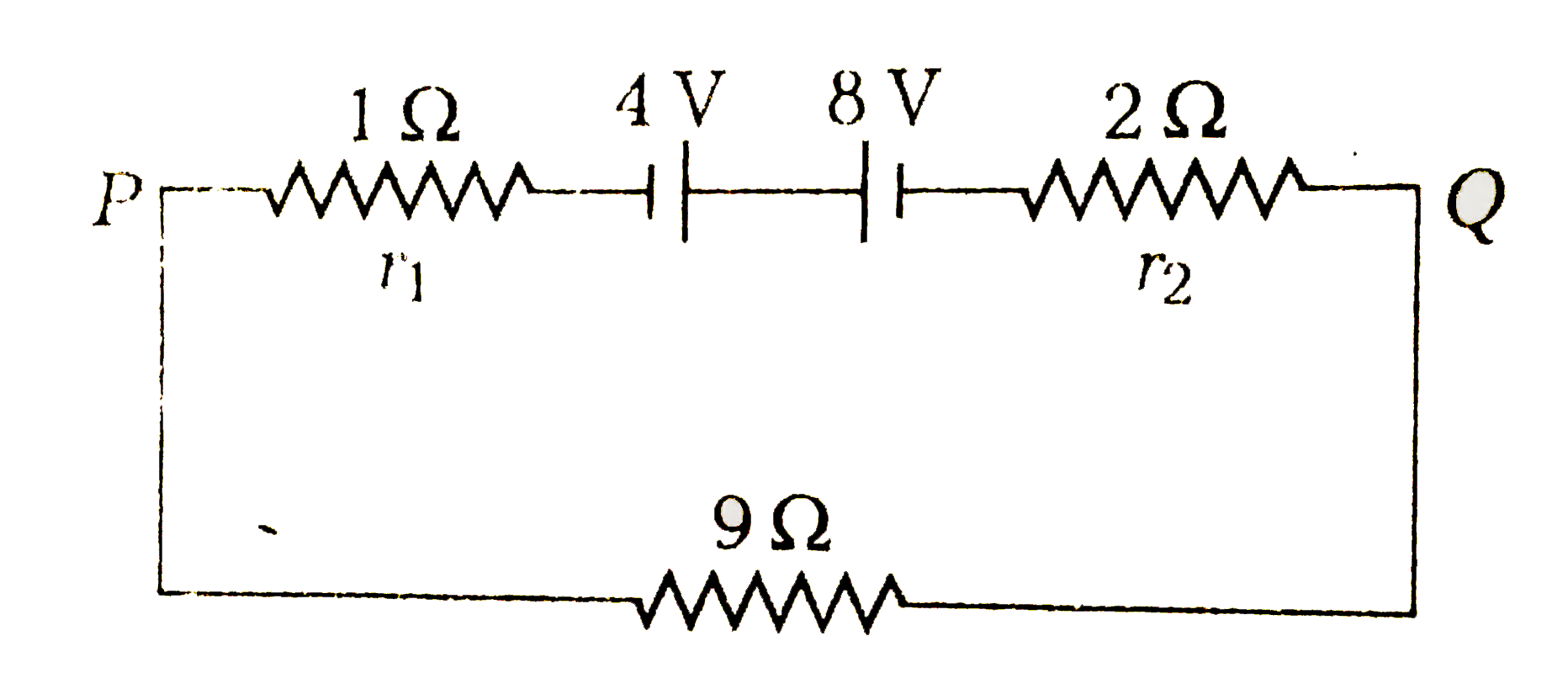
View SolutionTwo identical batteries, each of EMF 2V and internal resistance r=1Ω are connected as shown. the maximum power that can be developed across R using these batteries is :

View SolutionTwo batteries, one of emf 18 V and internal resistance 2 Ω and the other of emf 12 V and internal resistance 1Ω , are connected in parallel as shown in Fig. The voltmeter V will record a reading of

View SolutionTwo cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
View Solution