चित्र में, CD ।। AE तथा CY ।। BA
(i ) ΔCBX के बराबर वाले त्रिभुज का नाम बताइये।
(ii ) सिद्ध कीजिए कि (ΔZDE)=ar(ΔCZA)
(iii) सिद्ध कीजिए कि ar(BCZY)=ar(ΔEDZ)
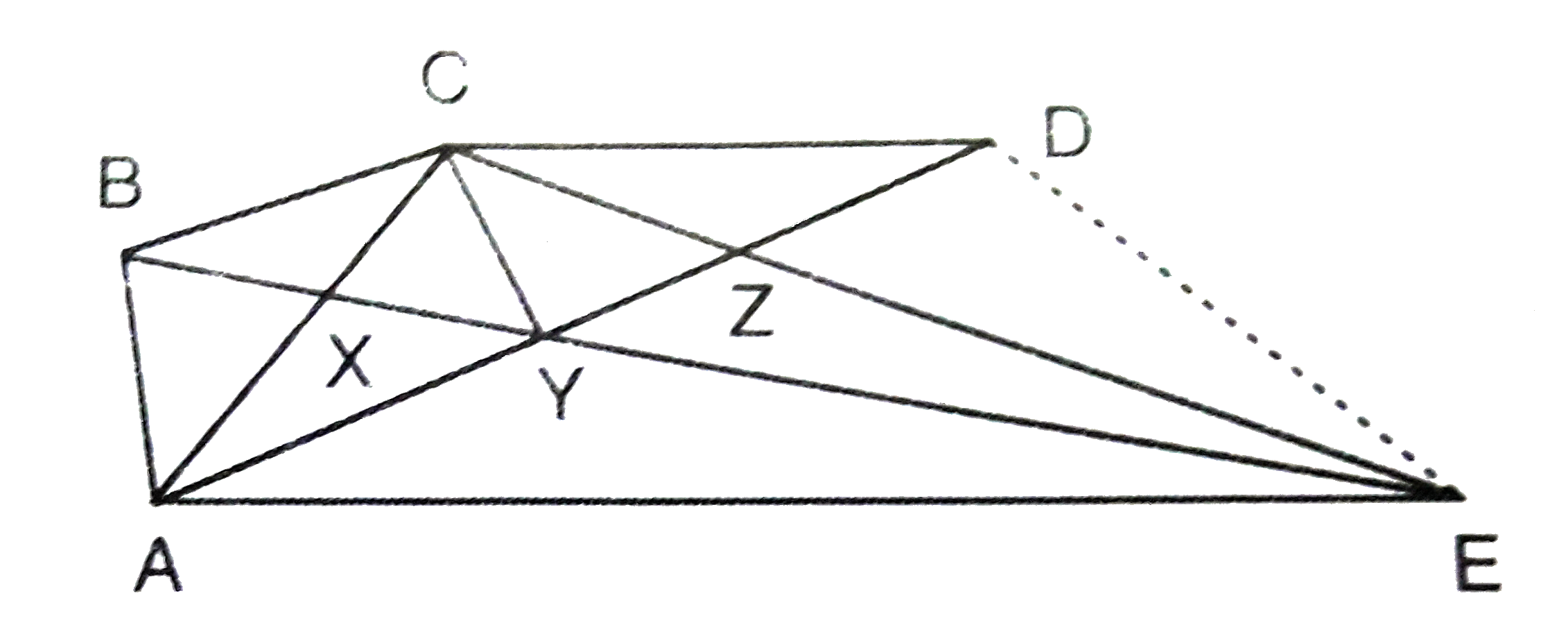
(ii ) त्रिभुज ADE तथा ACE एक ही आधार AE पर एक ही समांतर रेखाओं AE और CD युग्म के बीच स्थित है।
∴ar(ΔADE)=ar(ΔACE)
⇒ar(ΔADE)−ar(ΔAZE)=ar(ΔACE)−ar(ΔAZE)
⇒ar(ZDE)=ar(ΔACZ)
(iii ) त्रिभुज ACY तथा BCY एक ही आधार पर और एक ही समांतर रेखाओं CY और BA के बीच स्थित है।
∴ar(ΔACY)=ar(ΔBCY) ...(i)
अब, ar(ΔACZ)=ar(ΔZDE)
⇒ar(ΔACY)+ar(ΔCYZ)=ar(ΔEDZ)
⇒ar(ΔBCY)+ar(ΔCYZ)=ar(ΔEDZ) [(i) से ]
⇒ar(□BCZY)=ar(ΔEDZ)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अति लघुत्तरात्मक प्रश्न
9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.2
4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
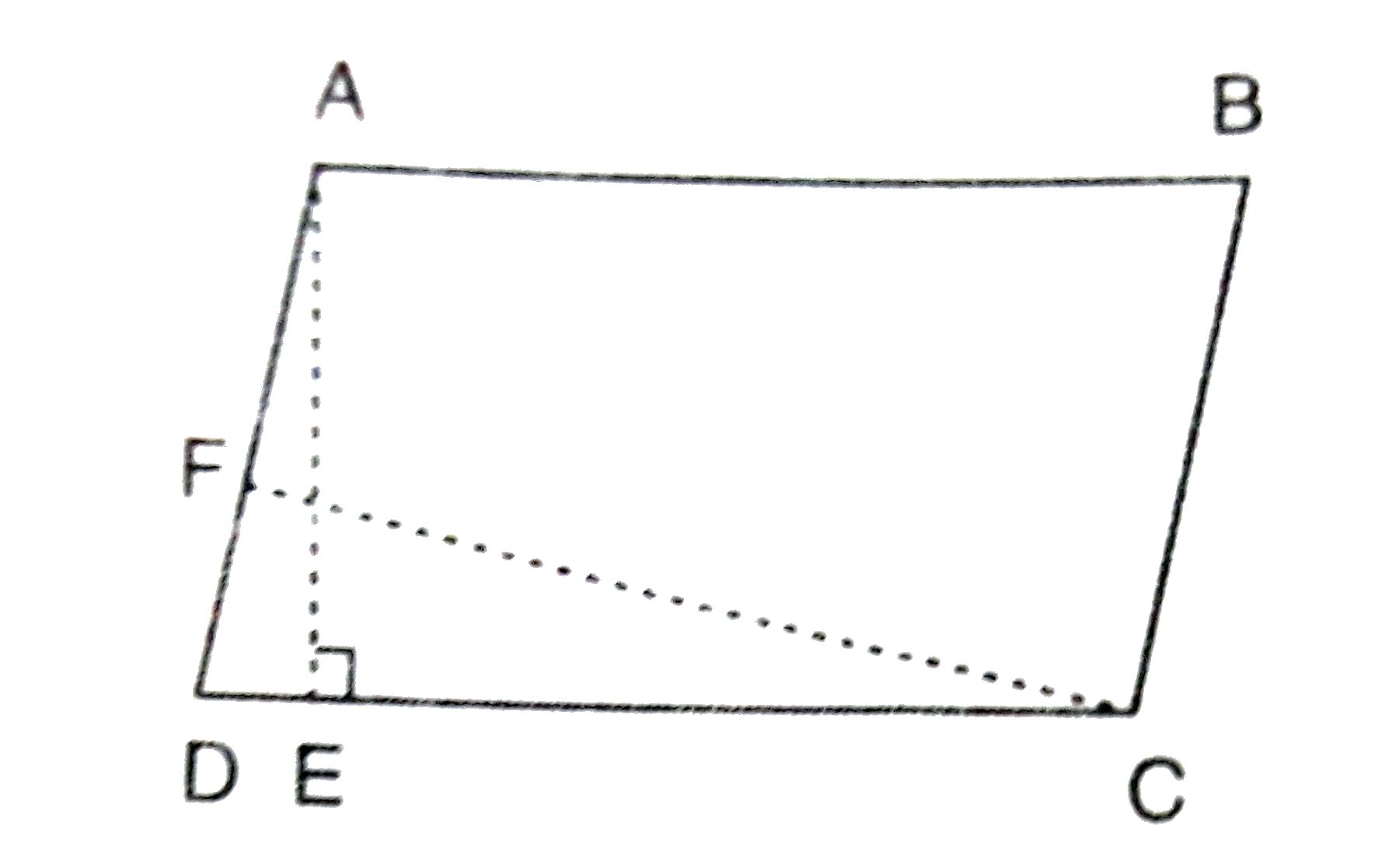
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
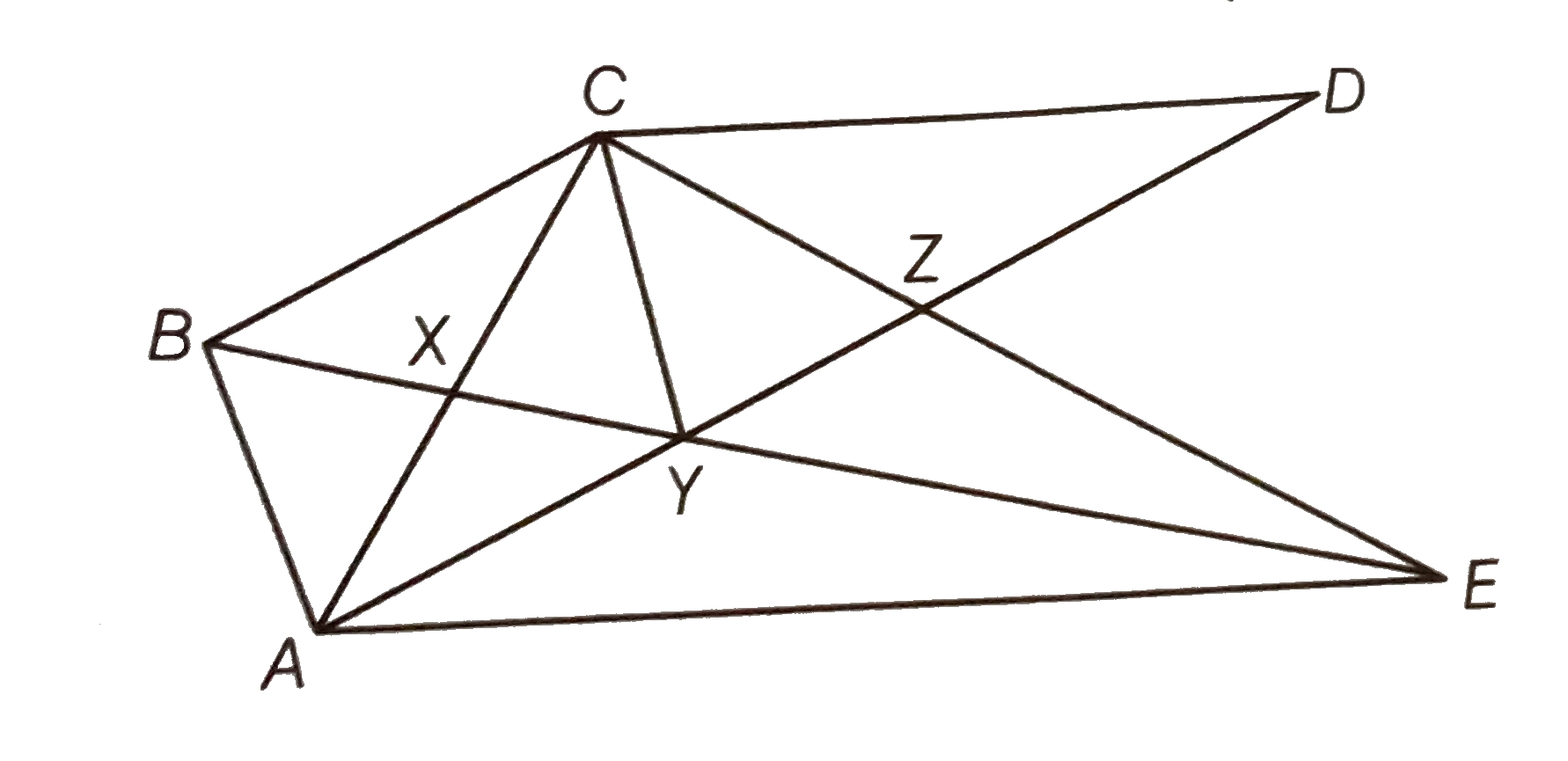
View SolutionIn figure, CD∣∣AE and CY∣∣BA. Prove that ar(ΔCBX)=ar(ΔAXY).
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionMatch the followings (column I with column II)
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/NCERT_BIO_XI_C03_E01_011_Q01.png" width="80%"gt
View Solution
