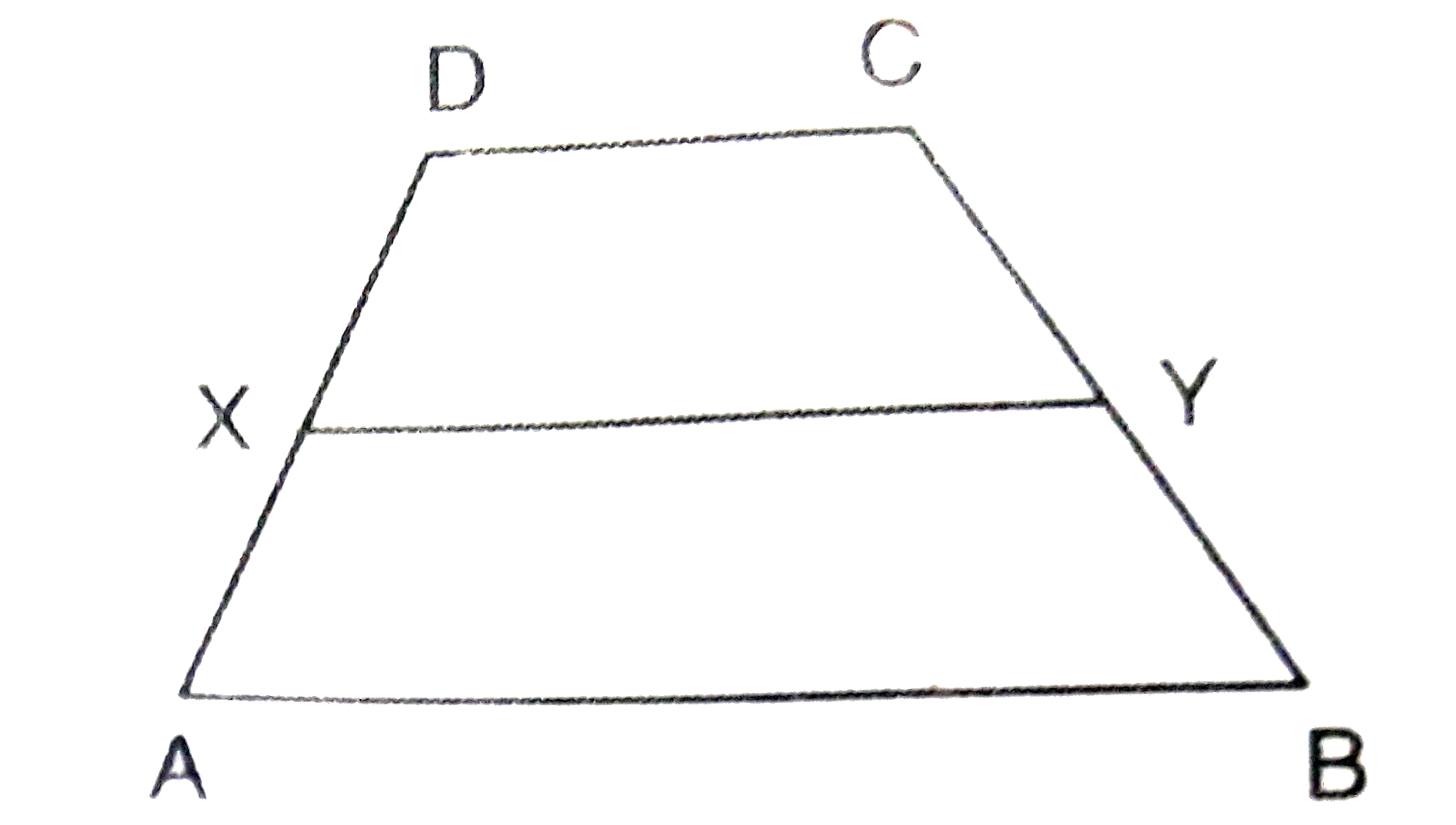
चित्र में, ABCD एक समलम्ब है जिसमें AB ।। BC तथा DC = 40 सेमी तथा AB = 60 सेमी यदि AD तथा BC के मध्य-बिंदु क्रमशः X तथा Y हो, तो सिद्ध कीजिए कि
(i) XY = 50 सेमी
(ii ) DCYX एक समलम्ब है।
(iii) ar(समलम्ब DCYX) =911ar(समलम्ब XYBA )
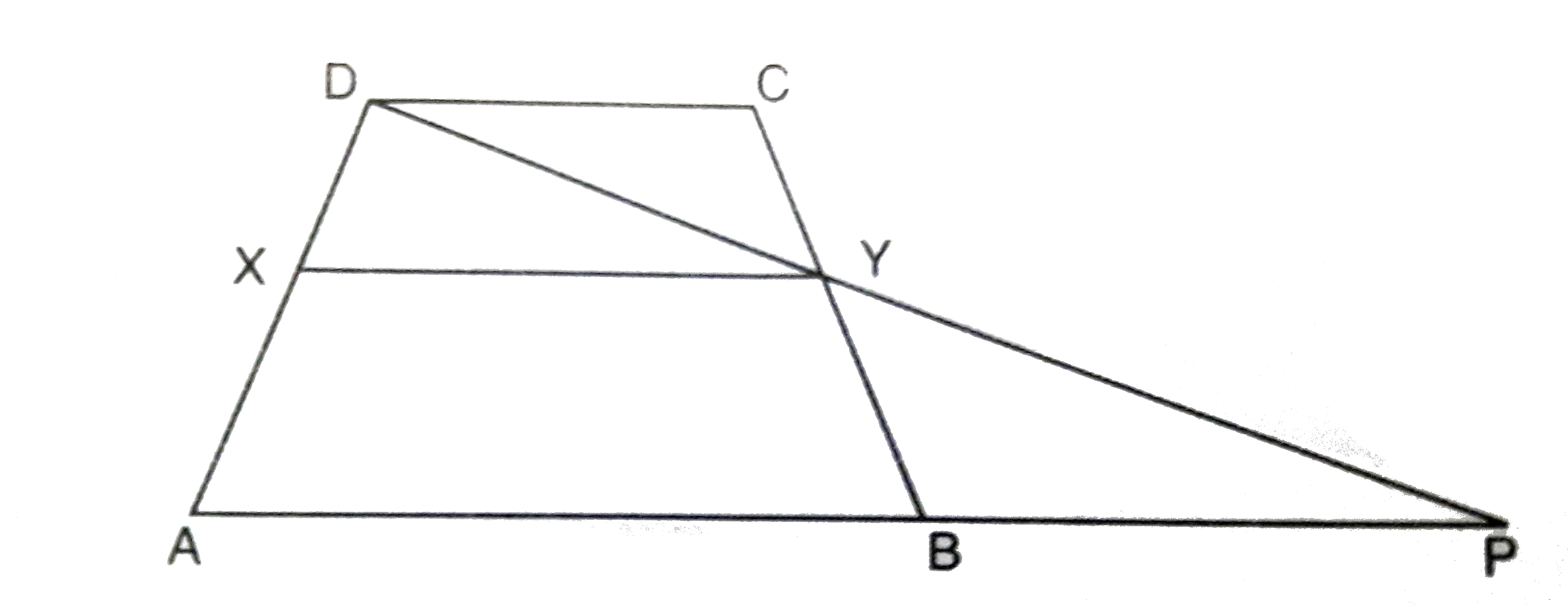
(i ) DY को मिलाकर आगे बढ़ाया जो AB के बढे भाग को P पर मिलता है।
ΔBYP तथा ΔCYD में
∠BYP=∠CYD [ शीर्षाभिमुख कोण ]
∠DCY=∠PBY [∵DC||AP]
तथा BY=CY
अतः कोण- भुजा-कोण सर्वांगसमता अभिगृहित से,
ΔBYP≅ΔCYD
⇒DY=YP तथा DC=BP
⇒Y,DP का मध्यबिंदु है ।
∴ XY || AP तथा XY=12AP
⇒XY=12(AB+BP)
⇒XY=12(AB+DC)⇒XY=12(60+40) सेमी =50 सेमी
(ii ) यह दिया है, कि
XY || AP [ उपरोक्त सत्यापित परिणाम से]
⇒ XY || AB तथा AB || DC [∵ ABCD एक समलम्ब है ]
⇒ XY || DC
⇒□DCYX एक समलम्ब है।
(iii ) चूँकि X और Y क्रमशः AD और BC के मध्य बिंदु हैं। अतः समलम्ब DCYX तथा ABYX एक ही ऊँचाई ( माना h सेमी ) के है।
अब, ar( समलम्ब DCYX ) =12(DC+XY)×h=12(40+50)h=45h वर्ग सेमी
ar( समलम्ब ABYX )=12(AB+XY)×h=12(60+50)h=55h वर्ग सेमी
∴ar(समलम्बDCYX)ar(समलम्बABYX)=45h55h=911
⇒ ar( समलम्ब DCYX)=911ar(समलम्ब ABYX)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अति लघुत्तरात्मक प्रश्न
9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.2
4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
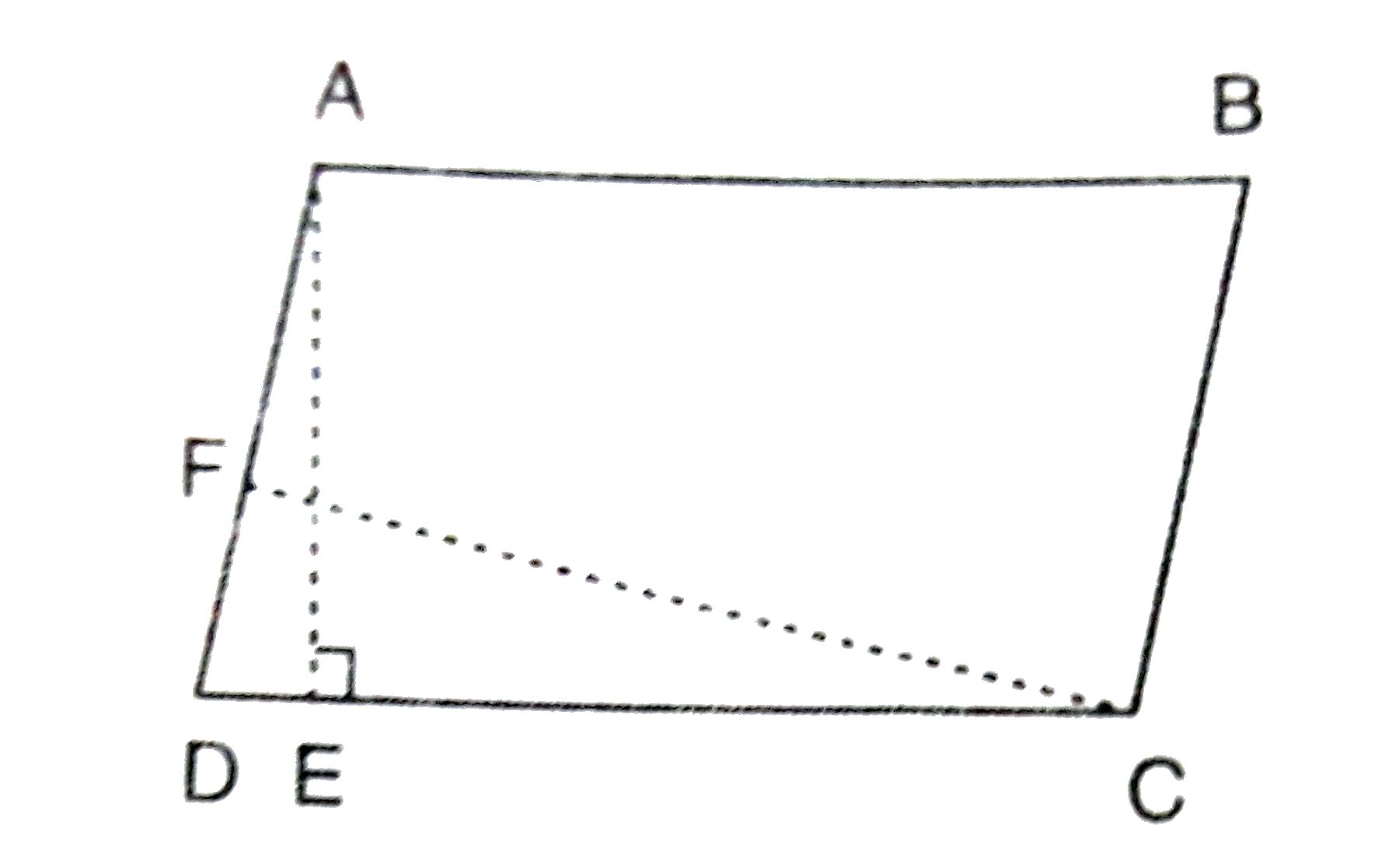
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionएक बेलन का व्यास 10 सेमी. तथा ऊंचाई 7 सेमी. है, तो बेलन का आयतन ज्ञात कीजिए।
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View SolutionABCD is a trapezium, in which AB||DC, DC=30cm And AB=50cm is. If X and Y are the mid-points of AD and BC respectively, prove that ar (DCYX) = (7)/(9) is ar (XYBA).
View SolutionABC is a triangle. AB =10cm and BC=16 cm AD=8 cm and is perpendicular to side BC. What is the length (in cm) of side AC? ABC एक त्रिभुज है। AB =10 सेमी तथा BC=16 सेमी है। AD=8 सेमी है तथा यह भुजा BC के समलम्ब है। भुजा AC का मान (सेमी. में) क्या है?
View SolutionABCD is a trapezium. Sides AB and CD. are parallel to each other.AB=6 cm, CD=18cm, BC=8cm and AD=12cm. A line parallel to AB divides the trapezium in two parts of equal perimeter. This line cuts BC at E and AD at F. If BE/EC = AF/FD, than what is the value of BE/EC? ABCD एक सम्लम्ब चतुर्भज है। भुजाएँ AB तथा CD एक दूसरे के समान्तर है। AB=6 सेमी. CD=18 सेमी. BC=8 सेमी. तथा AD= 12 सेमी. है। AB के समान्तर एक रेखा सम्लम्ब को दी बराबर परिमाप वाले हिस्से में काटता है। यह रेखा भुजा BC को E पर तथा AD को F पर काटती है। यदि BE/EC=AF/FD है, तो BE/EC का मान क्या है?
View SolutionABCD is a trapezium in which AB parallel to DC and its diagonals intersect at P. If AP = (3x - 1) cm, PC = (5x - 3) cm, BP = (2x + 1) cm and PD = (6x - 5) cm, then the length of DB is: ABCD एक समलम्ब है जिसमें AB, DC के समानांतर है तथा इसके विकर्ण P पर एक दूसरे को काठते हैं | यदि AP = (3x - 1) सेमी, PC = (5x - 3) सेमी, BP = (2x + 1) सेमी तथा PD = (6x - 5) सेमी है, तो DB की लंबाई क्या होगी ?
View Solutiontriangle ABC ~ triangle RQP and AB = 4 cm , BC = 6 cm and AC = 5 cm. If ar(triangle ABC) : ar (triangle PQR)=9:4 , then PQ is equals to : triangle ABC ~ triangle RQP है तथा AB = 4 सेमी, BC = 6 सेमी और AC = 5 सेमी है | यदि ar(triangle ABC) : ar (triangle PQR)=9:4 ,है, तो PQ किसके बराबर है ?
View Solution
