चित्र में, ABC तथा BDE समबाहु त्रिभुज इस प्रकार है कि BC का मध्य-बिंदु D है। यदि AE , BC को बिंदु F पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि
(i) ar(ΔBDE)=14ar(ΔABC)
(ii) ar(ΔBDE)=12(ΔBAE)
(iii) ar(ΔBFE)=2ar(ΔFED)
(iv) ar(ΔFED)=18ar(ΔAFC)
(v) ar(ΔABC)=2ar(DetlaABC)=2ar(ΔBEC)
(vi) ar(ΔBFE)=ar(ΔAFD)
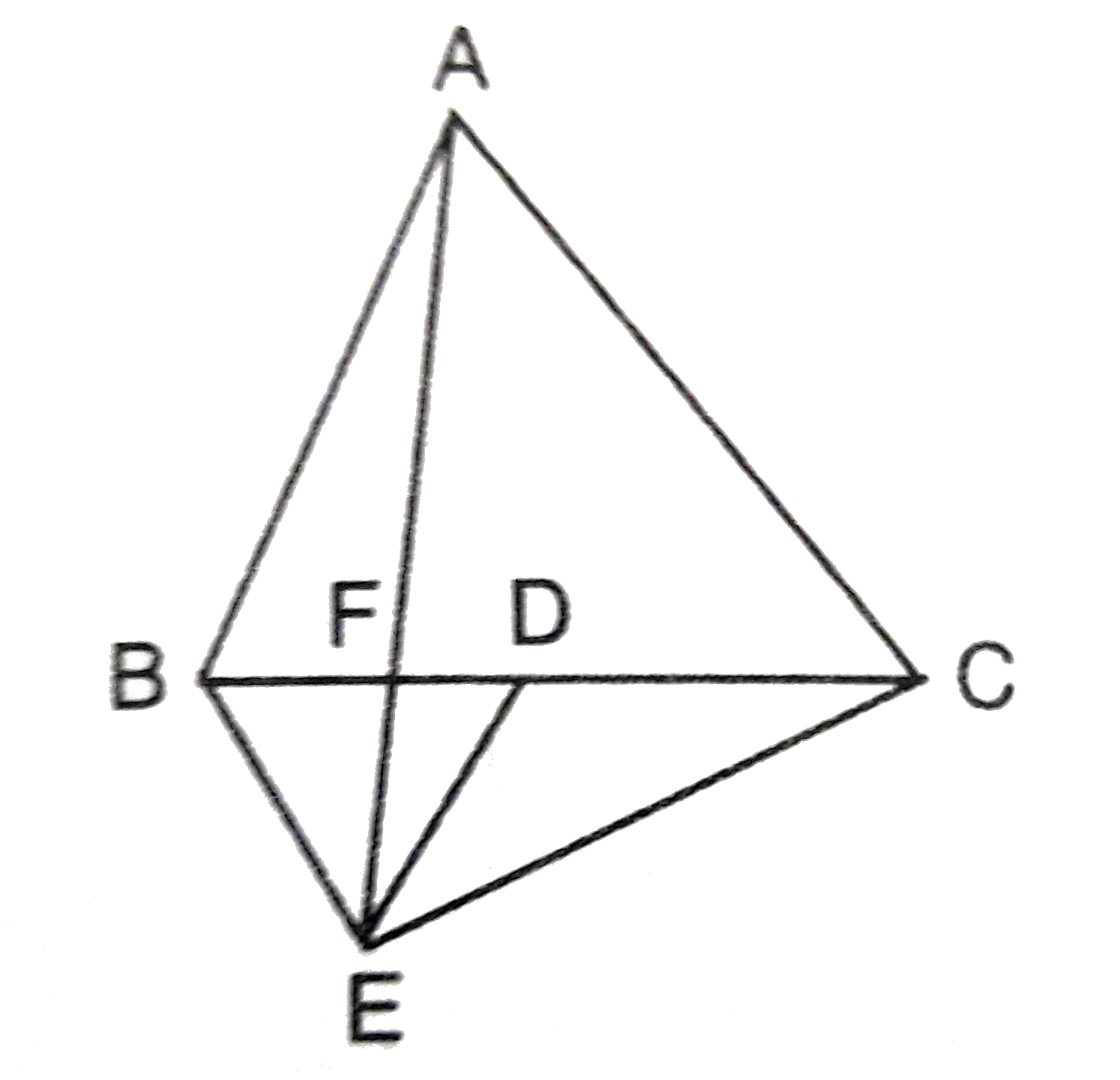
माना AB = BC = CA= x है। अतः BD=x2=DE=BE
(i ) स्पष्ट है कि
ar(ΔABC)=√34x2 तथा ar(ΔBDE)=√34(x2)2=14×√34x2
∴ar(ΔBDE)=14ar(ΔABC)
(ii ) यह दिया है कि त्रिभुज ABC और त्रिभुज BED समबाहु त्रिभुज है।
∴∠ACB=∠DBE=60∘
⇒ BE || AC
⇒ar(ΔBAE)=2ar(ΔBEC) ...(i)
⇒ar(ΔBAE)=2ar(ΔBDE) [∵ED,ΔEBC की एक माध्यिका है∴ar(ΔBEC)=2ar(ΔBDE)]
⇒ar(ΔBDE)=12ar(ΔBAE)
(iii ) चूँकि ΔABC एवं ΔBDE समबाहु त्रिभुज है।
∴∠ABC=60∘ तथा ∠BDE=60∘
⇒∠ABC=∠BDE
⇒ AB || DE
⇒ar(ΔBED)=ar(ΔAED)
⇒ar(ΔBED)−ar(ΔEFD)=ar(ΔAED)−ar(ΔEFD)
⇒ar(ΔBEF)=ar(ΔAFD)
(iv) चूँकि ED,ΔBEC की एक माध्यिका है।
∴ar(ΔBEC)=2ar(ΔBDE)
⇒ar(ΔBEC)=2×14ar(ΔABC) [ उपरोक्त (i ) से ar(ΔBDE)=14ar(ΔABC)]
⇒ar(ΔBEC)=12ar(ΔABC)
⇒(ΔABC)=2ar(ΔBEC)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अति लघुत्तरात्मक प्रश्न
9 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.2
4 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
यदि ABC व BDE दो समबाहु त्रिभुज इस प्रकार है कि बिंदु D भुजा BC का मध्य बिंदु है, तो त्रिभुज ABC और त्रिभुज BDE के क्षेत्रफल का अनुपात ज्ञात करो।
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है। AE⊥DC तथा CF⊥AD । यदि AB = 16 सेमी, AE = 8 सेमी तथा CF = 10 सेमी , तो AD का मान ज्ञात कीजिये ।
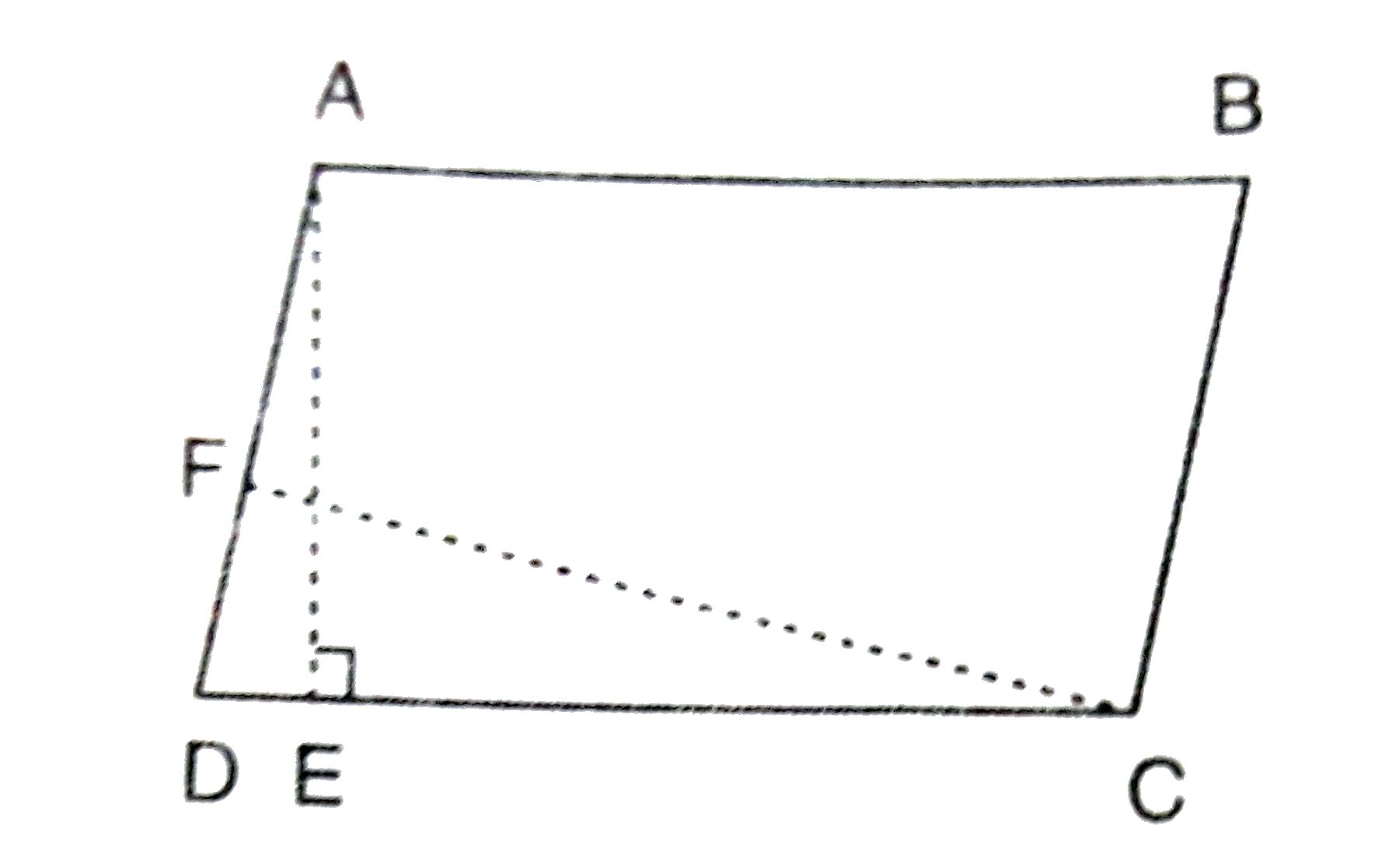
View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
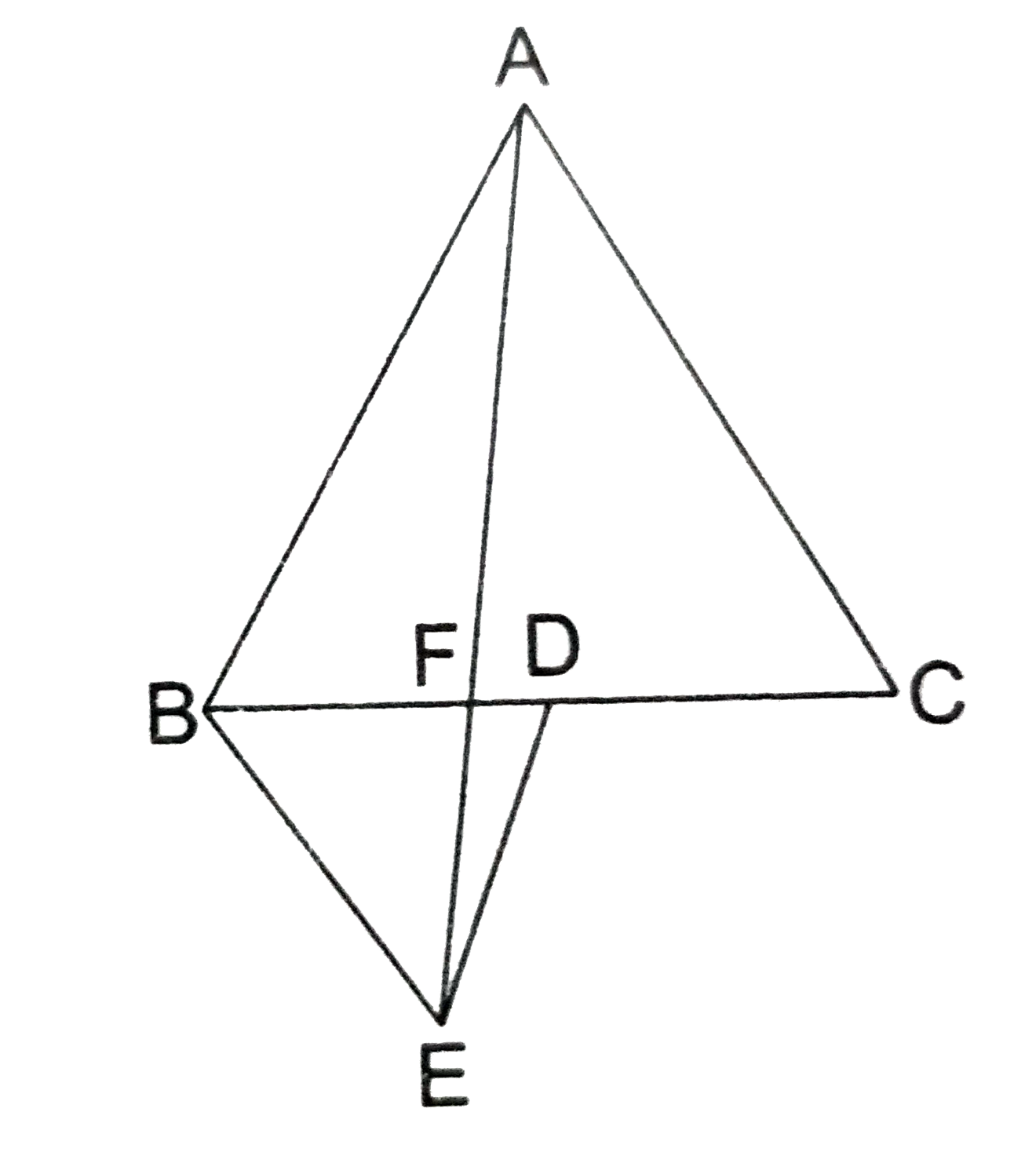
View Solutionदिए गए आकृति में ABC और BDF दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य बिंदु है |यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाई की
ar(BDF)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE) ltBrgt (iii) ar(ABC)=2ar(BEC)
(iv) ar(BEF)=ar(AFD) ltBrgt (v) ar(BEF)=2ar(FED)
(vi)ar(FED)=18ar(AFC)
View SolutionF,Cl, Br ,I and Ar are collectively known as ____________.
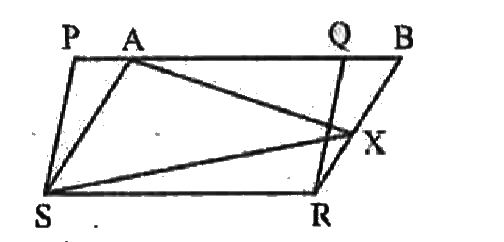
View SolutionIn, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
ar (PQRS) = ar (ABRS)
as (AXS) = 12 ar (PQRS)
View SolutionFactorise:
ar+br+at+bt
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
View Solutionआकृति में PQRS और ABRS समांतर चतुर्भज है तथा x भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि
ar(AXS)=12ar(PQRS)
View SolutionPQRS and ABRS are parallelograms and X is any point on the side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(ΔAXS)=12ar(PQRS)
View Solution
