An ant is at a corner of a cubical room of side a. The ant can move with a constant speed u. The minimum time taken to reach the farthest corner of the cube is
3au
√3au
√5au
(√2+1)au
The correct Answer is:C
To solve the problem of finding the minimum time taken by an ant to reach the farthest corner of a cubical room of side a while moving with a constant speed u, we can follow these steps:
Step 1: Understand the Geometry of the Problem
The ant starts at one corner of the cube (let's call it point A) and needs to reach the opposite corner (point B). The distance between these two points is the diagonal of the cube.
Step 2: Calculate the Distance
The distance d between two opposite corners of a cube can be calculated using the 3D distance formula. For a cube with side length a, the distance d is given by:
d=√a2+a2+a2=√3a2=a√3
Step 3: Relate Distance to Time
The time t taken to cover a distance d at a constant speed u can be expressed using the formula:
t=du
Step 4: Substitute the Distance
Substituting the expression for d into the time formula gives:
t=a√3u
Step 5: Conclusion
Thus, the minimum time t taken by the ant to reach the farthest corner of the cube is:
t=a√3u
The ant starts at one corner of the cube (let's call it point A) and needs to reach the opposite corner (point B). The distance between these two points is the diagonal of the cube.
The distance d between two opposite corners of a cube can be calculated using the 3D distance formula. For a cube with side length a, the distance d is given by:
d=√a2+a2+a2=√3a2=a√3
The time t taken to cover a distance d at a constant speed u can be expressed using the formula:
t=du
Substituting the expression for d into the time formula gives:
t=a√3u
Thus, the minimum time t taken by the ant to reach the farthest corner of the cube is:
t=a√3u
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Subjective
51 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct
6 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Assertion And Reason
12 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Six particles situated at the corners of a regular hexagon of side a move at a constant speed v. Each particle maintains a direction towards the particle at the next corner. Calculate the time the particles will take to meet each other.
View SolutionEight equal point charges each of charge 'q' and mass 'm' are placed at eight corners of a cube of side 'a'
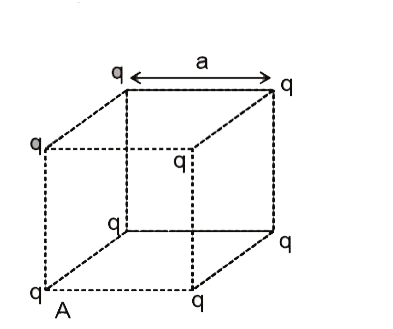
If all the charges are released at rest then find out their speed when they are at the corners of cube of side 2a.
View Solution
Knowledge Check
Four particles situated at the corners of a square of side ‘a’ move at a constant speed v. Each particle maintains a direction towards the next particle in succession. Calculate the time particles will take to meet each other.
AavBa2vCa3vD2a3vA car parked on a road side from sometimes , starts moving with a constant speed . Which of the following distance- time graph shows the motion of that car ?
A B
B C
C D
D
A car parked on a road side from sometime, starts moving with a constant speed. Which of the following distance-time graph shows the motion of that car ?
A B
B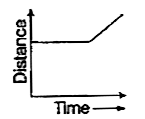 C
C D
D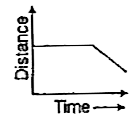
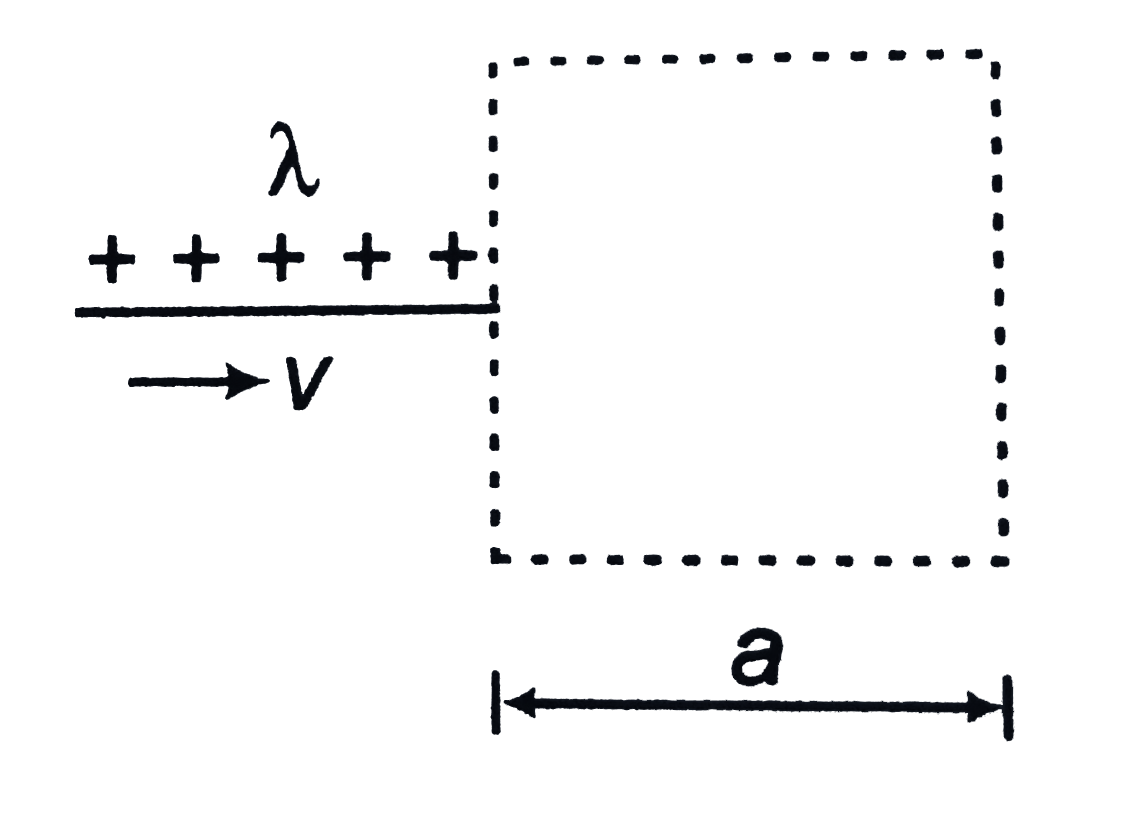
Figure shows an imaginary cube of side a. A uniformly charged rod of length a moves towards right at a constant speed v. At t=0 the right end of the just touches the left face of the cube. Plot a graph between electric flux passing through the cube versus time.
View SolutionIn the figure the top view of a compartment of a train is shown. A man is sitting at a corner 'B' of the compartment . The man throws a ball ( with respect to himself ) along the surface of the floor towards the corner 'D' of the compartment of the train. The ball hits the corner 'A' of the compartment, then find the time at which it hits A after the ball is thrown . Assume no other collision during motion and floor is smooth. The length of the compartment is given 'l' and the train is moving with constant acceleration 'a' in the direction shown in the figure.
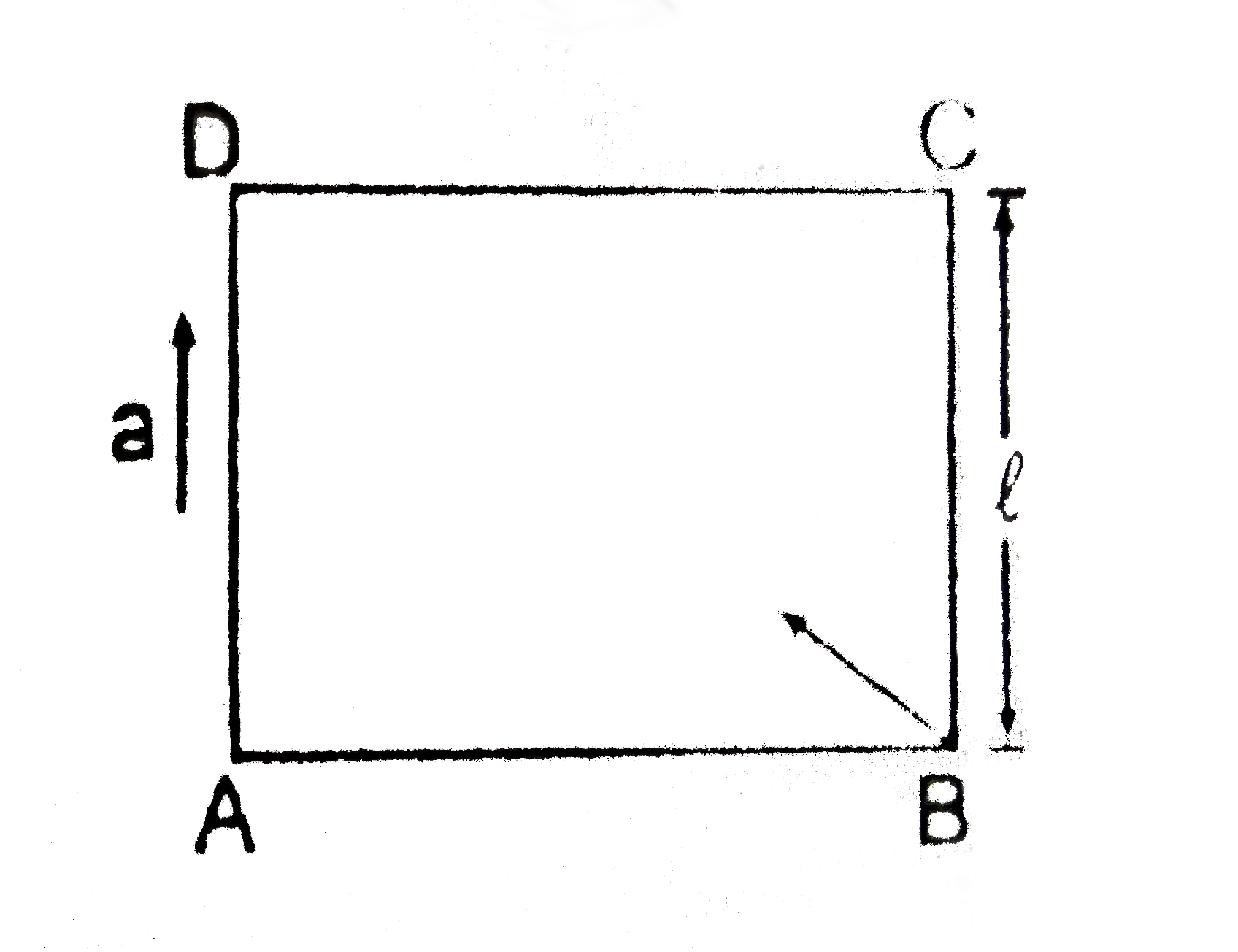
View SolutionAn insect fly start from one corner of a cubical room and reaches at diagonally opposite corner. The magnitude or displacement of the insect is 40√3 ft. Find the volume of cube.
View Solutionthe distance between two stations is 20 km. if a train moves with a constant speed of 60kmh−1 , then the time taken by the train moves with a constant speed of 60kmh−1 , then the time taken by the rain to reach the next station is _____
View SolutionThe distance between two stations is 20 km. If a train moves with a constant speed of 60 km h−1, then the time taken by the train to reach the next station is _____.
View Solution