Coefficient of friction between two block shown in figure ia μ=0.4. The blocks are given velocities of 2m/s and 8m/s in the directions figure. Find

(a) The time when relative motion between them will stop
(b) the common velocities of blocks upto that instant. (c) Displacement of 1kgand 2kg block upto that instant (g=10m/s2).
2kg block has relative motion towards right.Therefore , maximum friction will acts on it towards left
f=μN=(0.4)(1)(10)=4N
a1=41=4m/s2
a2=−42=2m/s2
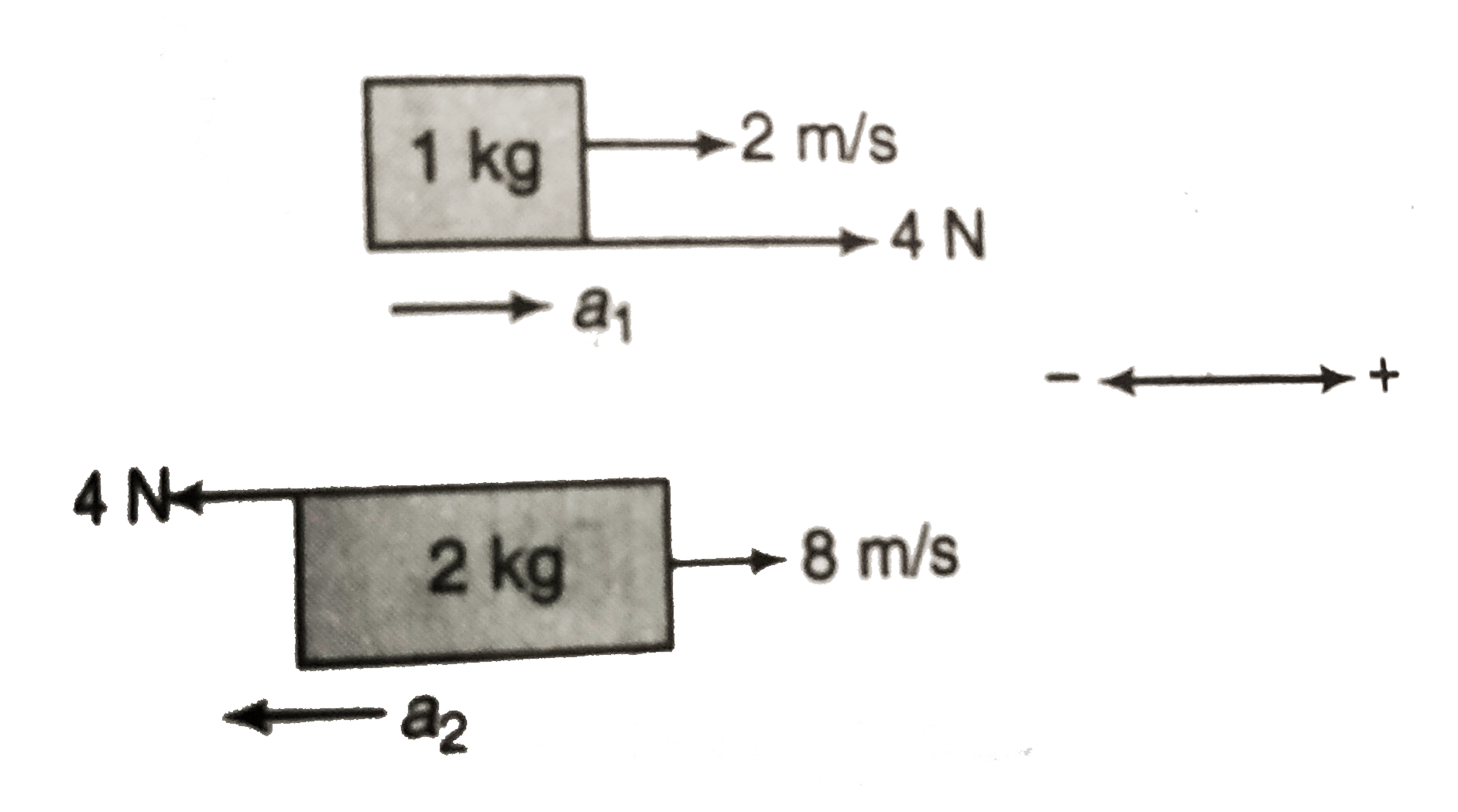
(b) Relative motion between them will stop when ,
v1=v1 ...(i)
∴u1+a1t=u2+a2t ...(ii)
∴2+4t=8−2t ...(iv) or t=1s
(b) Substituting value of 't' in Eq. (ii),either on RHS or on LHS common velocity =6m/s
( c) s1=u1t+12a1t2
=(2)(1)+12(4)(1)2=4m
s2=u2t+12a2t2
=(8)(1)+12(−2)(1)2=7m
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
Coefficient of friction between two blocks shown in Fig. 7.203 is μ=0.4 . The blocks are given velocities of 2 m/s and 8 m/s in the directions shown in figure . The time when relative motion between them will stop is ( in sec) . :

View Solutioncoefficient of friction between two blocks shown in figure is μ=0.6. The blocks are given velocities in the direction shown in figure. Find
(a) the time when relative motion between them is slopped.
(b) the common velocity of the two blocks.
(c) the displocement of 1kg and 2kg blocks upto that instant. (Takeg=10m/s2)

View Solution
Knowledge Check
In the figure two blocks are given velocities as shown. The lower block is very long. Find velocities of both the blocks when relative motion between them is ceased
 A2m/s (towards right)B1m/s (towards left)C2m/s (towards left)D1m/s (towards right)
A2m/s (towards right)B1m/s (towards left)C2m/s (towards left)D1m/s (towards right)In the figure shown, upper block is given a velocity of 6m/s and lower block. 3m/s. When relative motion between them is stopped
 AWork done by friction on upper block is −10JBWork done by friction on lower block +10JCNet work done by friction is zeroDAll of the above
AWork done by friction on upper block is −10JBWork done by friction on lower block +10JCNet work done by friction is zeroDAll of the aboveIn the figure shown, upper block is given a velocity of 6m/s and lower block. 3m/s. When relative motion between them is stopped
 AWork done by friction on upper block is negativeBWork done by frictoin on both the blocks is negativeCWork done by friction on lower block is negativeDWork done by friction on both the blocks is positive
AWork done by friction on upper block is negativeBWork done by frictoin on both the blocks is negativeCWork done by friction on lower block is negativeDWork done by friction on both the blocks is positive
A conveyor belt is moving with constant speed of 6m/s. A small block is just dropped on it.Coefficient of friction between the two is μ=0.3. Find

(a) The time when relative motion between them will stop
(b) Displacement of block upto that instant (g=10m/s2).
View SolutionThe coefficient of friction between the two blocks shown in the figure is μ=0.4 and between the lower block and the ground is zero. The blocks are given velocities of 2ms−1 and 8ms−1 respectively in the direction shown in the figure. In how much time (in seconds) the slipping between the blocks will stops ?
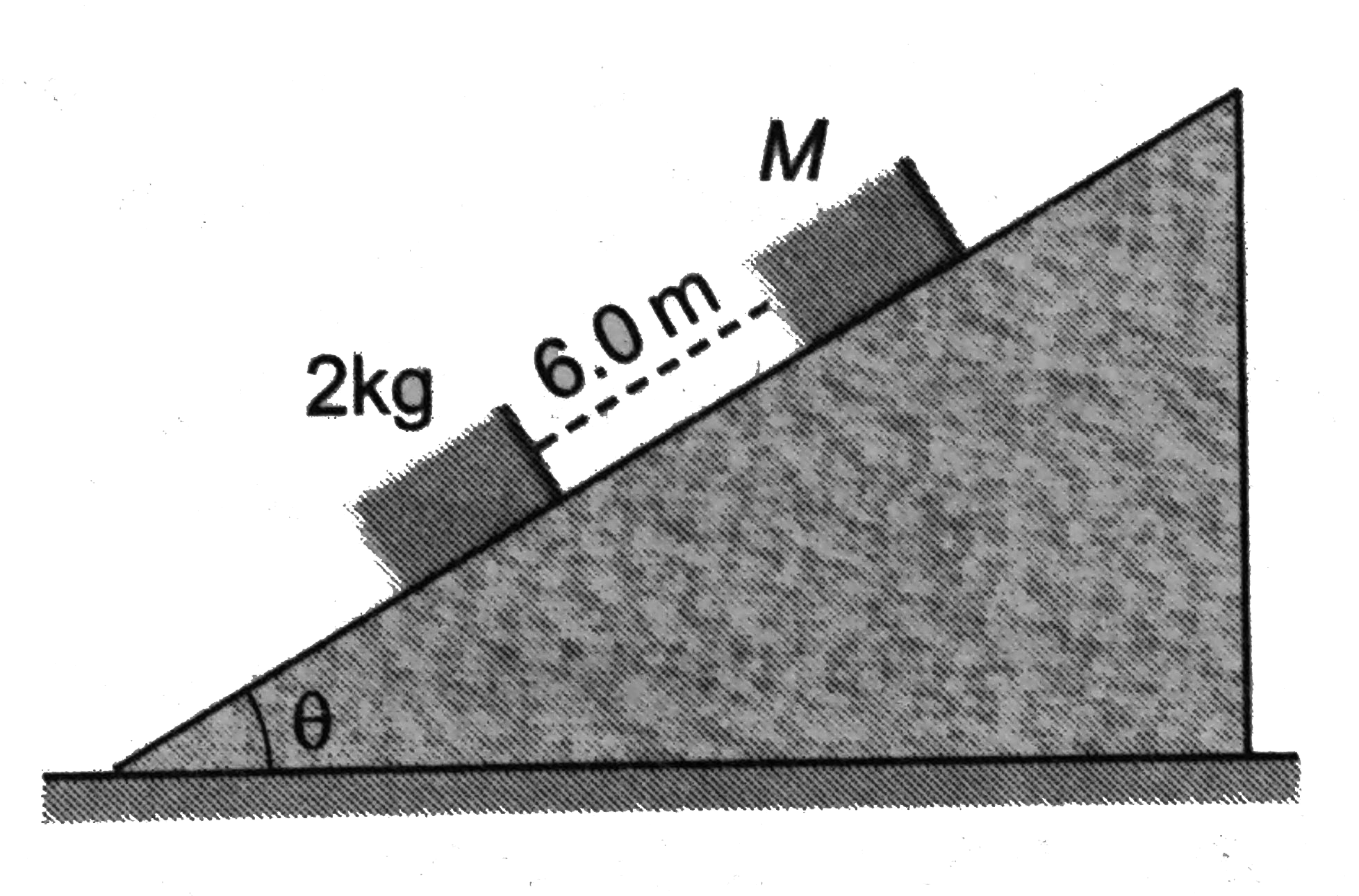
View SolutionTwo blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
View SolutionIn the figure shown upper block is given a velocity of 6m/s and lower block 3m/s. When relative motion between them is stopped.
 .
.
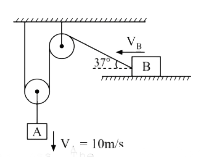
View SolutionIn the arrangement shown, velocity of block A is 10 m/s at a moment. Then the velocity of block B at this instant is :
View Solution