A uniform cube of mass m and slidea is resting in equilibrium on a rough 45∘ inclined surface. The distance point of application of normal reation measured from the lower edge of the cube is
zero
a3
a√2
a4
The correct Answer is:A
To solve the problem of finding the distance from the lower edge of the cube to the point of application of the normal reaction on a rough inclined surface, we will follow these steps:
1. Identify Forces Acting on the Cube:
- The weight of the cube, mg, acts vertically downwards.
- The normal force N acts perpendicular to the inclined surface.
- The frictional force f acts parallel to the inclined surface, opposing the tendency of the cube to slide down.
2. Determine the Angles:
- The inclined surface makes an angle θ=45∘ with the horizontal.
3. Break Down the Weight into Components:
- The component of the weight acting down the incline is mgsinθ.
- The component of the weight acting perpendicular to the incline is mgcosθ.
4. Equilibrium Conditions:
- Since the cube is in equilibrium, the sum of forces in both the perpendicular and parallel directions must be zero.
- In the perpendicular direction:
N=mgcosθ
- In the parallel direction:
f=mgsinθ
5. Static Friction:
- The frictional force f is equal to mgsinθ because the cube is not moving.
6. Calculate the Moments about the Center of the Cube:
- Let x be the distance from the center of the cube to the point of application of the normal force.
- The moment due to friction about the center (C) is:
Moment due to friction=f⋅A2=mgsinθ⋅A2
- The moment due to the normal force is:
Moment due to normal=N⋅x=mgcosθ⋅x
7. Set Up the Moment Equation:
- Since the cube is in equilibrium, the sum of moments about point C must be zero:
mgsinθ⋅A2−mgcosθ⋅x=0
8. Solve for x:
- Rearranging the equation gives:
mgsinθ⋅A2=mgcosθ⋅x
- Dividing both sides by mg (which cancels out) and substituting θ=45∘ (where sin45∘=cos45∘=1√2):
A2=x
- Thus, we find:
x=A2
9. Determine the Distance from the Lower Edge:
- The distance from the lower edge of the cube to the point of application of the normal reaction is:
Distance from lower edge=A−x=A−A2=A2
- Since the normal force acts at the lower edge, the distance from the lower edge is effectively:
0
Final Answer:
The distance from the lower edge of the cube to the point of application of the normal reaction is 0.
- The weight of the cube, mg, acts vertically downwards.
- The normal force N acts perpendicular to the inclined surface.
- The frictional force f acts parallel to the inclined surface, opposing the tendency of the cube to slide down.
- The inclined surface makes an angle θ=45∘ with the horizontal.
- The component of the weight acting down the incline is mgsinθ.
- The component of the weight acting perpendicular to the incline is mgcosθ.
- Since the cube is in equilibrium, the sum of forces in both the perpendicular and parallel directions must be zero.
- In the perpendicular direction:
N=mgcosθ
- In the parallel direction:
f=mgsinθ
- The frictional force f is equal to mgsinθ because the cube is not moving.
- Let x be the distance from the center of the cube to the point of application of the normal force.
- The moment due to friction about the center (C) is:
Moment due to friction=f⋅A2=mgsinθ⋅A2
- The moment due to the normal force is:
Moment due to normal=N⋅x=mgcosθ⋅x
- Since the cube is in equilibrium, the sum of moments about point C must be zero:
mgsinθ⋅A2−mgcosθ⋅x=0
- Rearranging the equation gives:
mgsinθ⋅A2=mgcosθ⋅x
- Dividing both sides by mg (which cancels out) and substituting θ=45∘ (where sin45∘=cos45∘=1√2):
A2=x
- Thus, we find:
x=A2
- The distance from the lower edge of the cube to the point of application of the normal reaction is:
Distance from lower edge=A−x=A−A2=A2
- Since the normal force acts at the lower edge, the distance from the lower edge is effectively:
0
The distance from the lower edge of the cube to the point of application of the normal reaction is 0.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.5
2 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
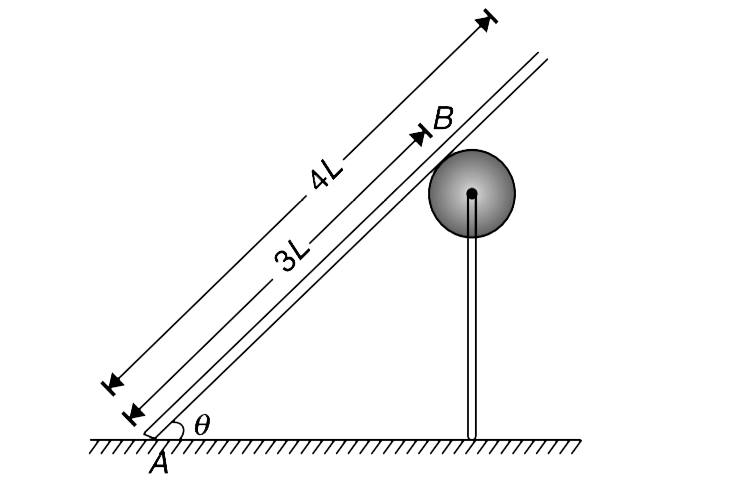
A uniform rod has mass M and length 4L. It rests in equilibrium with one end on a rough horizontal surface at A. At point B, at a distance 3L from A, it is supported by a fixed smooth roller. The rod just remains in equilibrium when θ=30∘
(a) Find the normal force applied by the horizontal surface on the rod at point A.
(b) Find the coefficient of friction between the rod and the surface.
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
View Solution
Knowledge Check
A horizontal force F=mg3 is applied on the upper surface of a uniform cube of mass m and slide a which is resting on a rough horizontal surface having μ=12. The distance between lines of action of mg and normal reation is
Aa2Ba3Ca4DNone of theseA horizontal force F=mg/3 is applied on the surface of a uniform cube of mass 'm' and side 'a' which is resting on a rough horizontal surface having μS=1/2. The distance between lines of action of 'mg' and normal reactiom 'N' is -
Aa/2Ba/3Ca/4DNoneA uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
A14mgB2mgC12mgD23mg
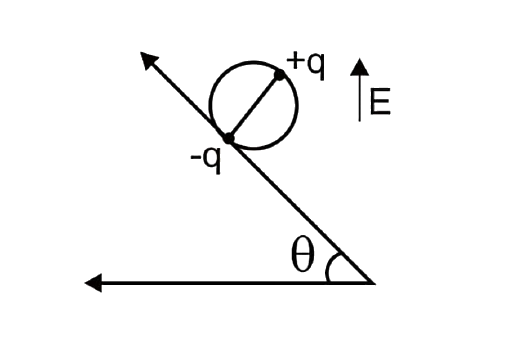
A wheel having mass m has charges +q and −q on diametrically opposite points. It remains in equilibrium on a rough inclined plane in the presence of a uniform vertical electric field E. The value of E is
View Solution
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
View SolutionA uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
View SolutionA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
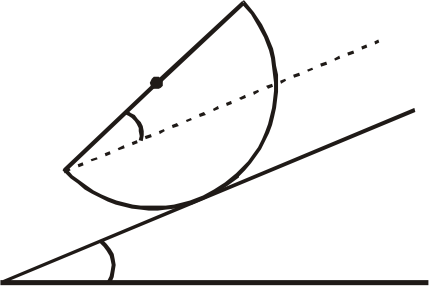
View SolutionA uniform thin hemispherical shell is kept at rest and in equilibrium on an inclined plane of angle of inclination θ=30∘ as shown inf figure. If the surface of the inclined plane is sufficiently rough to prevent sliding then the angle α made by the plane of hemisphere with inclined plane is :
View Solution
