A metal rod of length 1m is clamped at two points as shown in the figure. Distance of the clamp from the two ends are 5 cm and 15 cm, respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young's modulus of elasticity and density of aluminium are Y=1.6×1011Nm−2 and ρ=2500kgm−3 , respectively.

The correct Answer is:A, B, D
Speed of longitudinal waves in the rod,
v=√Yρ=√1.6×(1011)2500⎞⎟
⎟⎠=8000m/s
At the clamped position nodes will be formed.
Between the clamps integer number of loops will
be formed. Hence,
n1λ2=80
or n1λ=160.......(i)
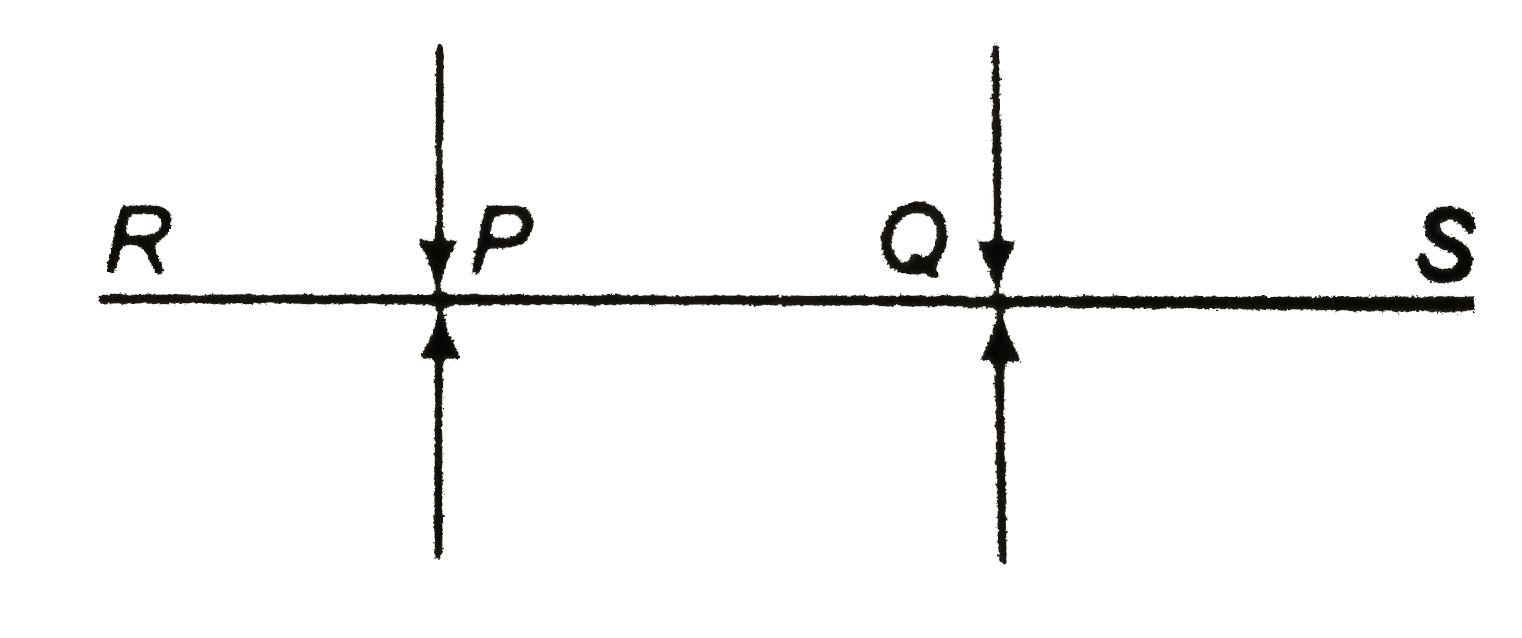
Between P and R, P is a fixed end and R is the free
end. It means the number of loops between P and
R will be odd multiple of λ4 . Then,
2n2−12λ2=5
or (2n2−1)λ=20 ...... (ii)
Also between Q and S, lt brgt (2n3−1)λ=60 ..........(iii)
From Eqs. (i) and (ii), we get
n12n2−1=16020=8 ........ (iv)
and from Eqs. (i) and (iii).
n12n3−1=16060=83 .......(v)
For minimum frequency n1n2andn3 should be
least from Eqs. (iv) and (v).
We get, n1=8,n2=1,n3=2
λ=202n2−1=20cm [from Eq. (ii)]
= 0.2 m
∴fmin=vλ=80000.2
= 40 kHz.
Next higher frequency corresponds to
n1=24,n2=2
and n3=5
f=120kHz
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:Level 2 Single Correct
Explore 15 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:Level 2 More Than One Correct
Explore 6 Videos
- SUPERPOSITION OF WAVESBook:DC PANDEYChapter:SUPERPOSITION OF WAVESExercise:Level 1 Subjective
Explore 24 Videos
- SOUND WAVESBook:DC PANDEYChapter:SOUND WAVESExercise:Exercise 19.7
Explore 4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBook:DC PANDEYChapter:THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESExercise:Medical entrance gallary
Explore 30 Videos
Similar Questions
A metal rod length l=100 cm is changed at two points A and B as shown in fig. Distance of each clamp from neared and is a=30 cm. if density and Young's modulus of elesticity of rod material are ρ=9000kg/m3 and Y=144Gpa, respectively, calculate minimum and next higher frequency of natural longitudinal oscillations of the rod.
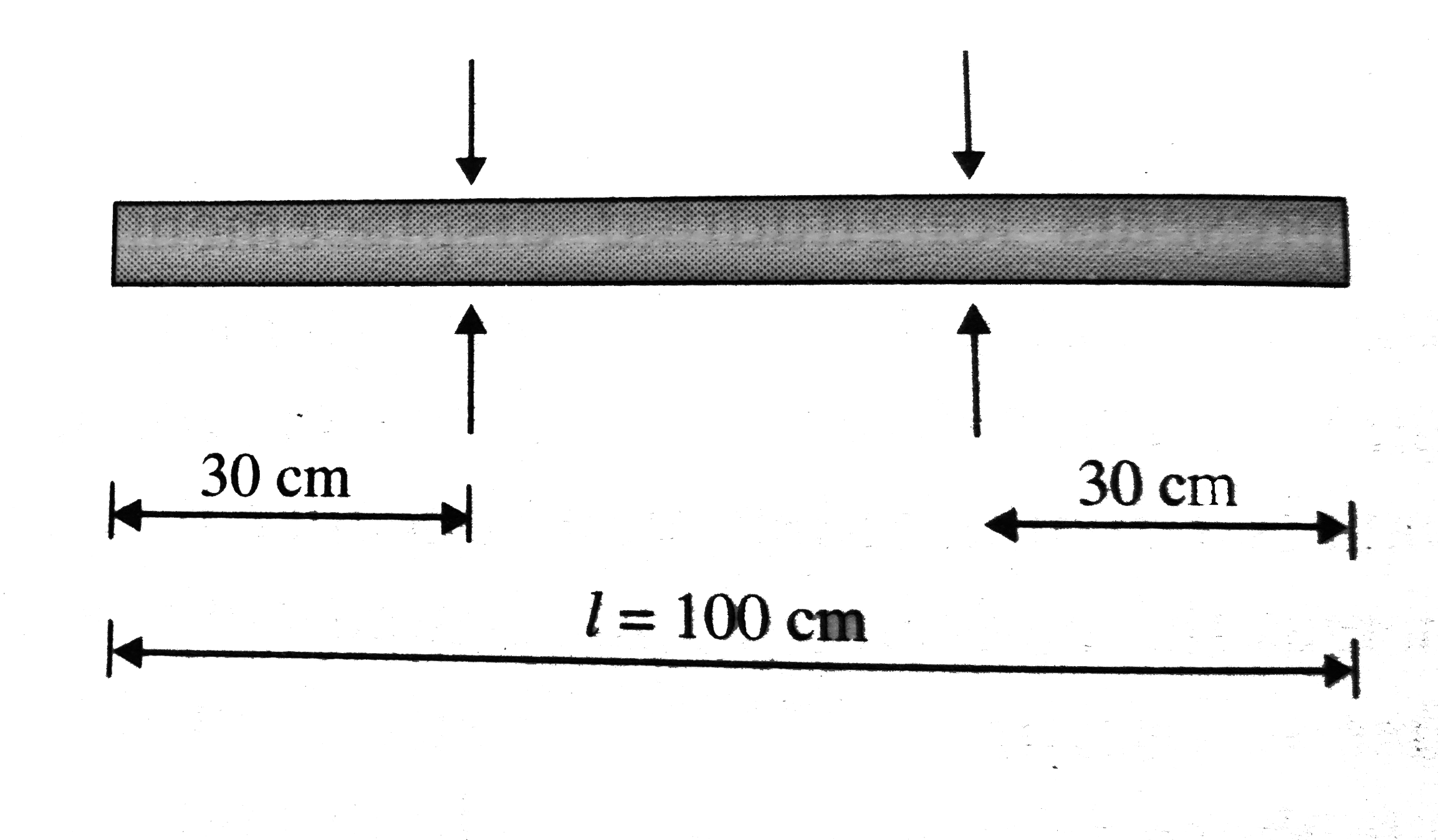
View SolutionA metal rod length l=100 cm is changed at two points A and B as shown in fig. Distance of each clamp from neared and is a=30 cm. if density and Young's modulus of elesticity of rod material are ρ=9000kg/m3 and Y=144Gpa, respectively, calculate minimum and next higher frequency of natural longitudinal oscillations of the rod.

View Solution
Knowledge Check
A metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec isA11√3π×10−6B11√2π×10−6C10√3π×10−6D10√2π×10−6A metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing stress developed in the rod isA140.8π×104cos(112πx+π)cos(22π×103t)B140.8π×104sin(112πx+π)cos(22π×103t)C128π×104cos(5πx+π)cos(20π×103t)D128π×104sin(5πx+π)cos(20π×103t)A metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. Young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing displacements of particles about their mean positions isAs−4×106cos(11π2x)cos(22π×103t)Bs=4×10−6cos(11π2x)sin(22π×103t)Cs=4×10−6cos(5πx)cos(20π×103t)Ds=4×10−6cos(5πx)sin(20π×103t)
A rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA suructural steel rod has a radius of 10mm and a length of 1m. A 100 kN force stretches it along its length. Calculate (a) the stress (b) elongation, and (c ) percentage strain on the rod. Given that the Young's modulus of elasticity of structural steel is 2.0×1011Nm−2.
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec is
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing stress developed in the rod is
View Solution
