A metal rod length l=100 cm is changed at two points A and B as shown in fig. Distance of each clamp from neared and is a=30 cm. if density and Young's modulus of elesticity of rod material are ρ=9000kg/m3 and Y=144Gpa, respectively, calculate minimum and next higher frequency of natural longitudinal oscillations of the rod.
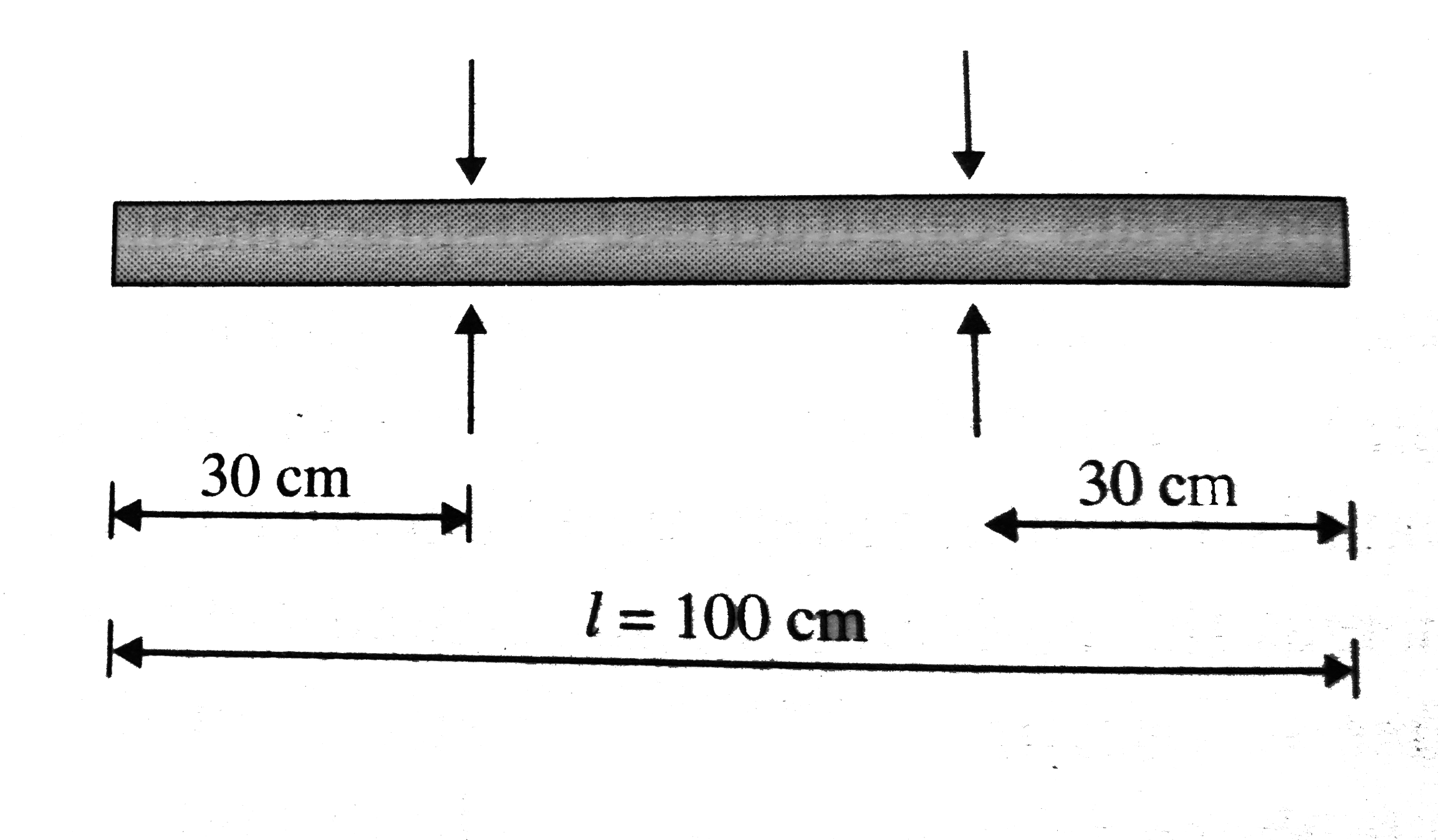
Speed of longitudinal waves in the rod is
v=√Yρ=4000m/s
Since points AandB are clamped , therefore , nodes are formed at these points or rod oscillates with integer number of loops in the middle part . Let number of these loops be m .
Since , length of each loop is λ/2 , therefore ,
mλ/2=(1−2a)
or mλ=80cm (i)
Since the ends of the rod are free, therfore , antinodes are formed at each end of the rod or at one end of each end part is an antinode and at the other end is a node . It means that number of loops in each end part will be an odd multiple of half . Let these be (2n−1)/2 where n is an integer. Then,
(2n−12)λ2=aor(2n−1)λ=120cm (ii)
Dividing Eq. (i) by Eq. (ii),
m(2n−1)=23 (iii)
Minimum possible frequency corresponds to maximum possible wavelength , hence , minimum number of loops.
Hence , from Eq. (iii) , for minimum frequency m should be wqual to 2and(2n−1) should be equal to 3orn=2.
Substituting m=2 in Eq . (i), Maximum wavelength λ0=40cm
Minimum frequency ,
f0=vλ0=10KHz
Next higher frequency corresponds to next higher integer values of mandn which satisfy Eq. (iii). Hence , for this case m=6and(2n−1)=9orn=5.
Substituting m=6 in Eq. (i) ,
λ=806cmor403cm
Therefore , next higher frequency ,
f1=vλ=30Hz
( It means rod oscillates with odd harmonics.)


Similar Questions
A metal rod of length 1m is clamped at two points as shown in the figure. Distance of the clamp from the two ends are 5 cm and 15 cm, respectively. Find the minimum and next higher frequency of natural longitudinal oscillation of the rod. Given that Young's modulus of elasticity and density of aluminium are Y=1.6×1011Nm−2 and ρ=2500kgm−3 , respectively.
 View Solution
View SolutionA uniform rod of length 20 cm is clamped at the two points A and B as shown. Then the fundamental frequency of longitudinal vibration of the rod is (Y=2×1011N/m2,ρ=8×103kg/m3)
 View Solution
View Solution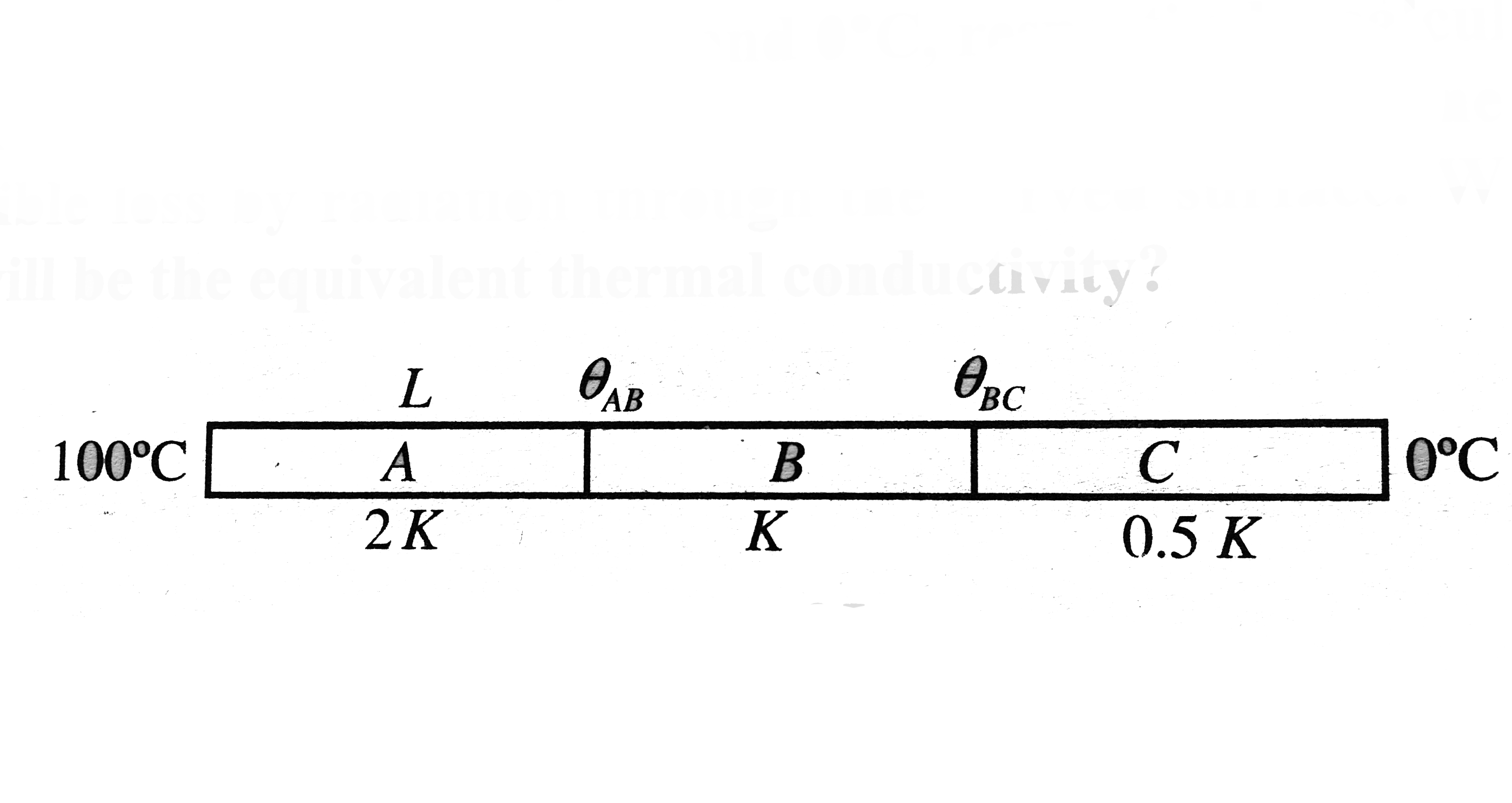
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?View SolutionA rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA granite rod of 60 cm length is clamped at its middle point and is set into longitudinal vibrations. The density of granite is 2.7×103kg/m3 and its Young’s modulus is 9.27×1010 Pa. What will be the fundamental frequency of the longitudinal vibrations ?
View SolutionAn aluminum rod having a length 100 cm is clamped at its middle point and set into longitudinal vibrations. Let the rod vibrate in its fundamental mode. The density of aluminum is 2600 kg/m3 and its Young's modulus is 7.8×1010N/m2. The frequency of the sound produced is :-
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec isView SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing stress developed in the rod isView SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing displacements of particles about their mean positions is.View Solution

