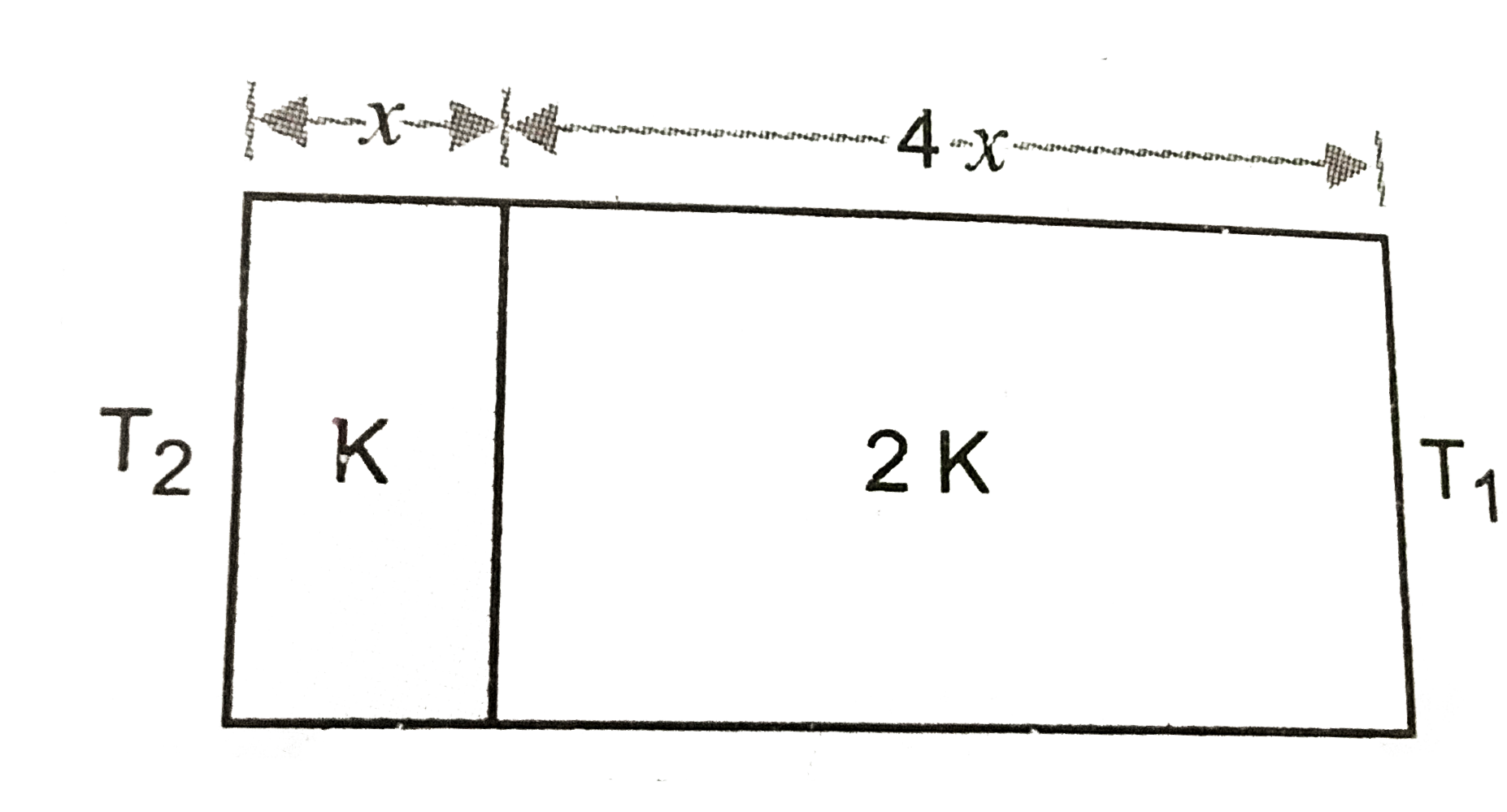
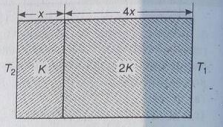
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-
![The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T(2) and T(1)(T(2)gtT(1)). The rate of heat of heat transfer through the slab, in ? steady state is [(A(T(2)-T(1))/(x)]f, with f equal to :-](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E09_013_Q01.png)
1
1/2
2/3
1/3
The correct Answer is:D
For slab in series , we have
Req=R1+R2=xKA+4x2KA=3xkA
Now , in a steady state rate of heat transfer throught the slab is given by .
dQdt=T2−T1Req=(T1−T1)3xKA ...(i)
Given dQdt=(A(T2−T1)x)f ....(ii)
Comparing (i) and (ii) we get f=1/3
Topper's Solved these Questions
Similar Questions
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
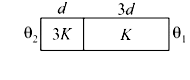
View Solution
Knowledge Check
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)Kx)f, with f equals to
 A1B1/2C2/3D1/3
A1B1/2C2/3D1/3The temperature of the two outer surfaces of a composite slab consisting of two materials having coefficient of thermal conductivity K and 2K and thickness x and 4x respectively are T2 and T1(T2>T1). The rate of heat transfer through the slab in steady state is (AK(T2−T1)x)f. where, f is equal to
 .A1B1/2C2/3D1/3
.A1B1/2C2/3D1/3
Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materails having coefficients of two materails having coefficients of termal conductivity K and 2K and thickness x and 4x, respectively, are T2andT1(T1>T1). The rate of heat transfer through the slab, in a steady state is (A(T2−T1)K2)f, with f equal to

View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View Solution
