L and M are mid points of two equal chords AB and CD of a circle with center O. Prove that ∠OLM=∠OML and ∠ALM=∠CML
PQ=SR
PQ2=SR2
XQ=YR
now ∠OCM is an isoceles ∠~∠O
now∠ALM=∠ALO−∠OLM
=90−∠OLM
∠CML=∠CMO−∠OML=90−∠OML
by comparing the 2 equations
so ∠OLM=∠OML
so, ∠ALM=∠CML
Similar Questions
L and M are mid-point of two equal chords AB and CD of a circle with centre O . Prove that ∠OLM= ∠OML (ii) ∠ALM= ∠CML
View SolutionL and M are mid-point of two equal chords AB and CD of a circle with centre O . Prove that ∠OLM= ∠OML (ii) ∠ALM= ∠CML
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :
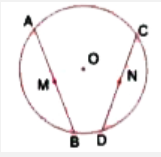
∠AMN=∠CNM.
View SolutionM and N are the mid-points of two equal chords AB and CD respectively of a circle with centre O. Prove that :

(i) ∠BMN=∠DNM
View SolutionThe locus of the mid points of all equal
chords in a circle is :
View SolutionAB and CD are equal chords of a circle whose center is O,
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the given figure, P is the mid-point of arc APB and M is the mid-int of chord AB of a circle with centre O. Prove that PM⊥AB
View Solution
