A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O'.
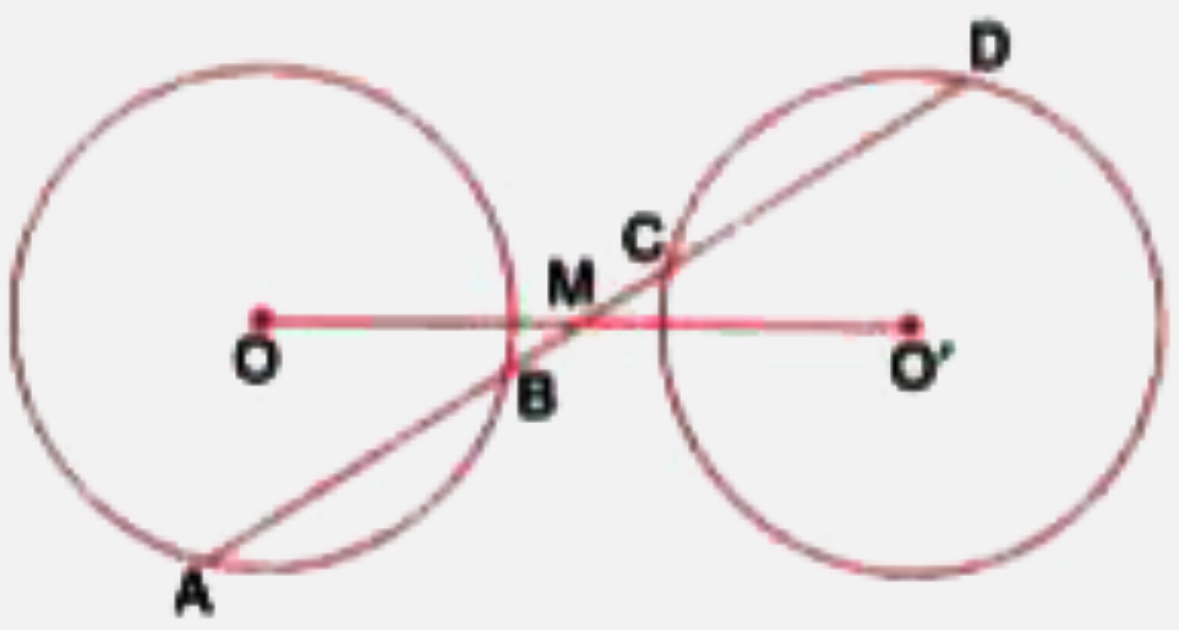 >
>
Prove that the chords AB and CD, which are intercepted by the two circles, are equal.
Step by step video & image solution for A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centres O and O'. > Prove that the chords AB and CD, which are intercepted by the two circles, are equal. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(C)
29 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(A)
14 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
A straight line is drawn cutting two equal circles and passing through the mid-point M of the joining their centres O and O'.
Prove that the chord AB and CD, which are intercepted by the two circles, are equal
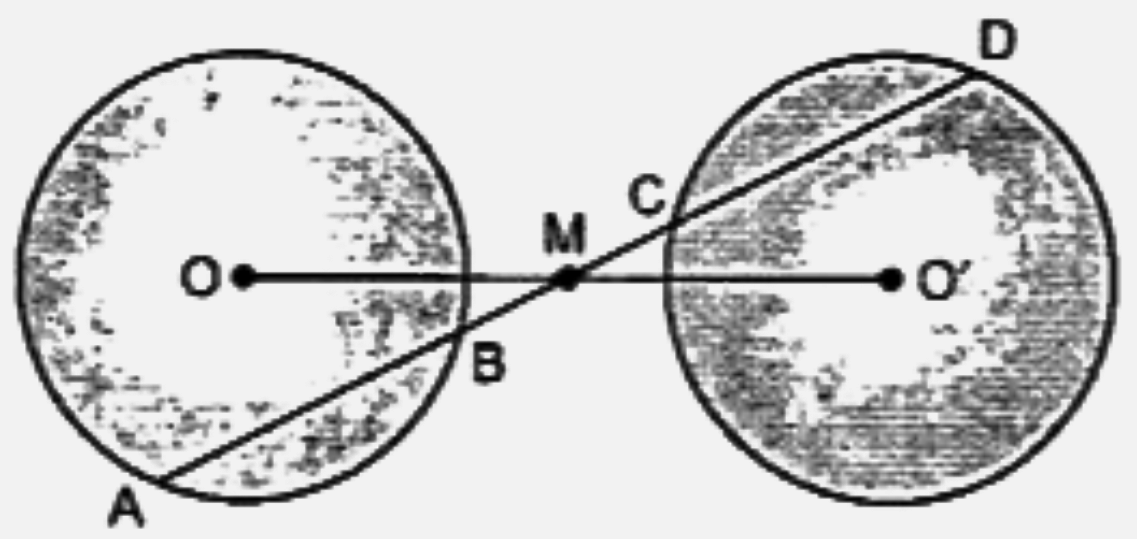
View SolutionThe line which cuts off equal-intercept from the axes and pass through the point (1,−2) is.
View SolutionProve that the tangent lines drawn from the outer point to the circle are equal? Or
View SolutionThe line joining the mid-points of two chords of a circle passes through its centre. Prove that the chords are parallel.
View SolutionIf two intersecting chords of a circle make equal angles with the diameterpassing through their point of intersection, prove that the chords are equal
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View SolutionProve that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
View Solution(Converse of Theorem 3) The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.
View Solution
