A plank is held at an angle α to the horizontal on two fixed supports A and B. The plank can slide against the supports (without friction) because of the weight Mg sinα. The acceleration and direction in which a man of mass m should move so that the plank does not move are

gsinα(1+mM) down the incline
gsinα(1+Mm) down the incline
gsinα(1+mM) up the incline
gsinα(1+Mm) up the incline
The correct Answer is:B
Free-body diagram of man and plank is given below.

For plank to be at rest, applying Newton's second law to plank along the incline
Mgsinα=f ..(i)
And applying Newton's second law to man along the incline,
mgsinα+f=ma...(ii)
⇒a=gsinα(1+Mm) down the incline.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Multiple Correct
Explore 11 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Assertion-reasoning
Explore 15 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Subjective
Explore 15 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionA man can move on a horizontal plank supported symmetrically as shown. The variation of normal reaction on support A with distance x of the man from the end of the plank is best represented by :
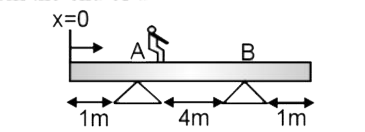
View Solution
Knowledge Check
A solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
A14maB32maCmaD12maA plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2A plank A of mass M rests on a smooth horizontal surface over which it can move without friction A cabe B of mass m lies on the plank at one edge .The coefficient of friction between the plank and the cube is μ The size of cube is very small in comparison to the plank.

At what force F applied to the plank in the horizontal direction will be cube begin to slide towards the other end of the plank?AF>μ(m+M)gBF>0.5μ(m+M)gCF=0.5μ(m+M)gDF=μ(m+M)g
Two balls are placed as shown in Fig. on a "weightless" support formed by two smooth inclined planes each of which forms an angle α with the horizontal. The support can slide without friction along a horizontal plane. The upper ball of mass m1 i s released. Determine the condition under which the lower ball of mass m2 tarts "climbing" up the support.

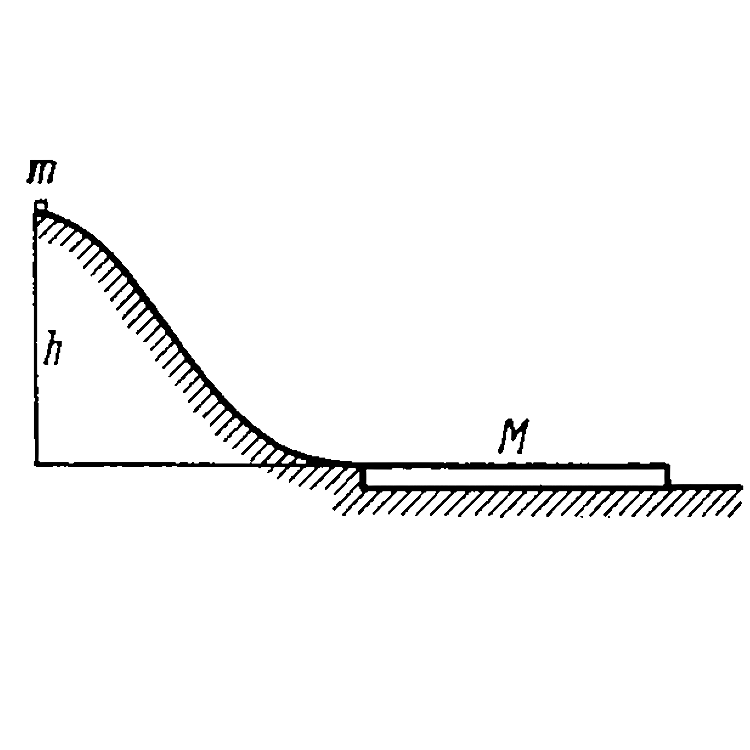
View SolutionA small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
View SolutionA plank of mass M is placed on a rough horizontal surface and a contant horizontal force F is applied on it . A man of mass m runs on the plank find the range of acceleration of the man that the plank does not move on the surface is μ .Assume that the does not slip on the plank

View SolutionIn the figure shown a plank of mass m is lying at rest on a smooth horizontal surface. A cylinder of same mass m and radius r is rotated to an angular speed w0 and then gently placed on the plank. It is found that by the time the slipping between the plank and the cylinder cease, 50% of total kinetic energy of the cylinder and plank system is lost. Assume that plank is long enough and um is the coefficient of friction between the cylinder and the plank.
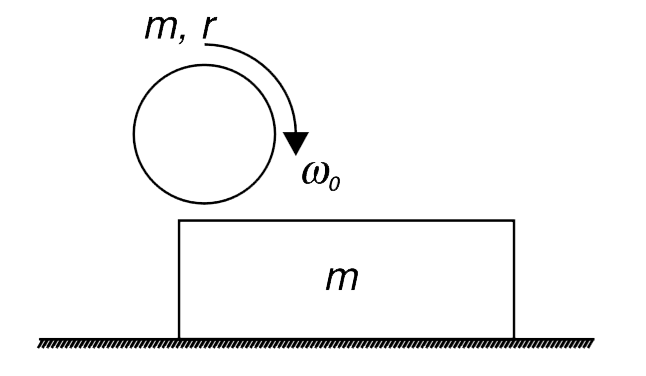
(a) Find the final velocity of the plank.
(b) Calculate the magnitude of the change in angular momentum of the cylinder about its centre of mass.
(c) Distance moved by the plank by the time slipping ceases between cylinder and plank.
View SolutionA plank A of mass M rests on a smooth horizontal surface over which it can move without friction A cabe B of mass m lies on the plank at one edge .The coefficient of friction between the plank and the cube is μ The size of cube is very small in comparison to the plank.
In what time will the cube fall from the plank if the length of the latter is l?

View Solution
