A small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
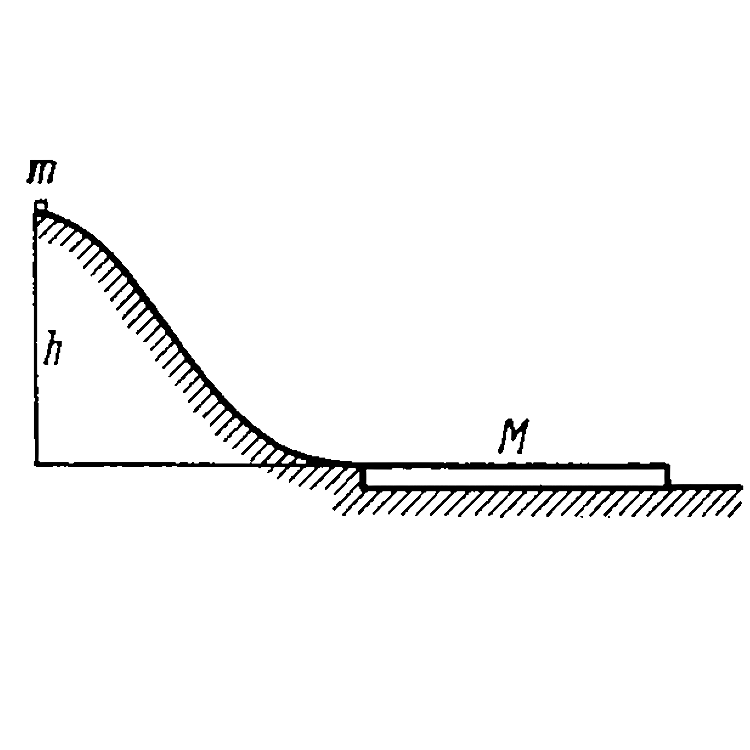
(a) When the disc slides and comes to a plank, it has a velocity equal to v=√2gh. Due to friction between the disc and the plank the disc slows down and after some time the disc moves in one piece with the plank with velocity v′ (say).
From the momentum conservation for the system (disc+plank) along horizontal towards right:
mv=(m+M)v′ or v′=mvm+M
Now from the equation of the increment of total mechanical energy of a system:
12(M+m)v′2−12mv2=Afr
or, 12(M+m)m2v2(m+M)2−12mv2=Afr
so, 12v2[m2M+m−m]=Afr
Hence, Afr=−(mMm+M)gh=−μgh
(where μ=mMm+M=reduced mass)
(b) We look at the problem from a frame in which the hill is moving (together with the disc on it) to the right with speed u. Then in this frame the speed of the disc when it just gets onto the plank is, by the law of addition of velocities, ¯v=u+√2gh. Similarly the common speed of the plank and the disc when they move together is
¯v=u+mm+M√2gh.
Then as above ¯¯¯Afr=12(m+M)¯v2−12m¯v2−12Mu2
=12(m+M){u2+2mm+Mu√2gh+m2(m+M)22gh}−12(m+M)u2−12m2u√2gh−mgh
We see that ¯¯¯Afr is independent of u and is in fact just 0μgh as in (a). Thus the result obtained does not depend on the choice of reference frame.
Do not however that it will be in correct to apply "conservation of energy" formula in the frame in which the hill is moving. The energy carried by the hill is not negligible in this frame. See also the next problem.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
A planet of mass M moves along a circle around the Sun with velocity v=34.9km/s (relative to the heliocentric reference frame). Find the period of revolution of this planet around the Sun.
03:22View SolutionA thin uniform rod AB of mass m=1.0kg moves translationally with acceleration w=2.0m/s2 due to two antiparallel forces F1 and F2 (figure). The distance between the points at which these forces are applied is equal to a=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
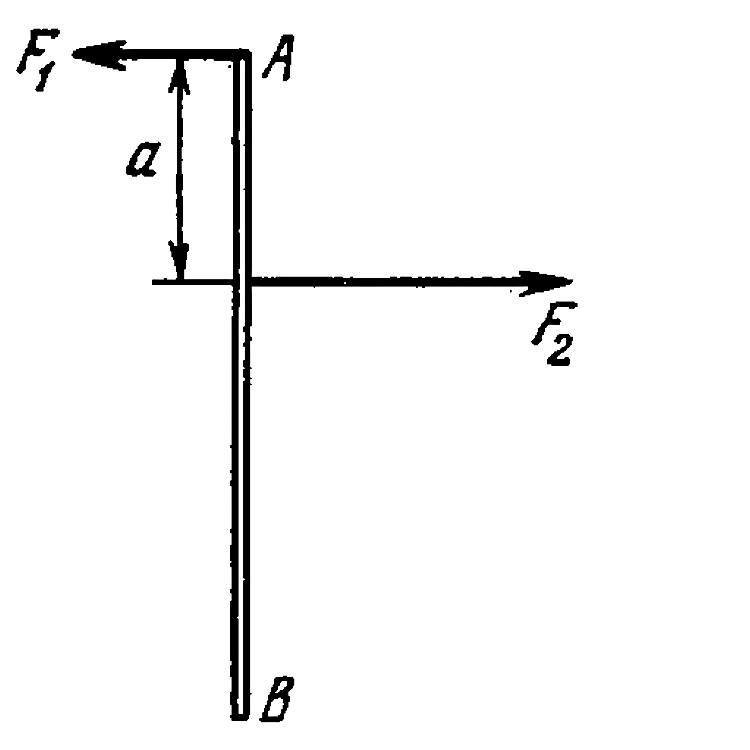 08:05View Solution
08:05View SolutionAn aerostat of mass m starts coming down with a constant acceleration w. Determine the ballast mass to be dumped for the aerostat to reach the upward acceleration of the same magnitude. The air drag is to be neglected.
05:08View SolutionAn electromagnetic wave of frequency v=3.0MHz passes from vacuum into a dielectric medium with permittivity ε=4.0. Then
05:08View SolutionCalculate what fraction of gas molecules
(a) traverses without collisions the distances exceeding the mean free path λ ,
(b) has the free path values lying within the inerval from λ to 2λ.View SolutionA solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is mu and that between the plank and the ground is mu//4 . Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc. Acceleration of the plank is
06:46View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc. Force of friction between the disc and the plank is
04:17View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown, The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F. The magnitude of acceleration of plank is
02:55View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,

The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of angular acceleration of the disc is04:28View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
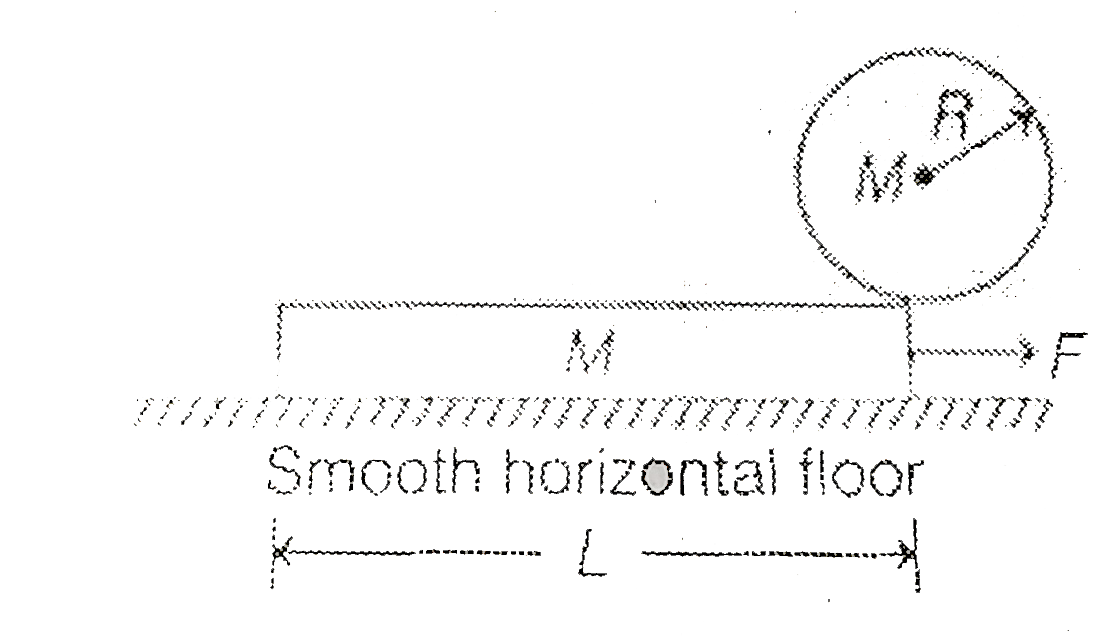
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The distance travelled by centre of disc from its initial position till the left end of plank comes vertically below the centre of disc is05:26View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc
 05:13View Solution
05:13View SolutionA small disc of mass m slides down a smooth hill of height h without initial velocity and gets onto a plank of mass M lying on the horizontal plane at the base of the hill. (figure). Due to friction between the disc and the plank the disc slows down and, beginning with a certain moment, moves in one piece with the plank.
(1) Find the total work performed by the friction forces in this process.
(2) Can it be stated that the result of obtained does not depend on the choice of the reference frame?
 04:54View Solution
04:54View SolutionA solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
07:09View Solution

