A small ball attached with one end of an inextensible thread is moving in a vertical circle. Ratio of its maximum to minimum velocity is $2 : 1$ .
Calculate tension in thread and acceleration of the ball at the moment when velocity of the ball is directed vertically downward. $(g = 10 m s^{- 2})$ .

Video Solution

Text Solution

Verified by Experts

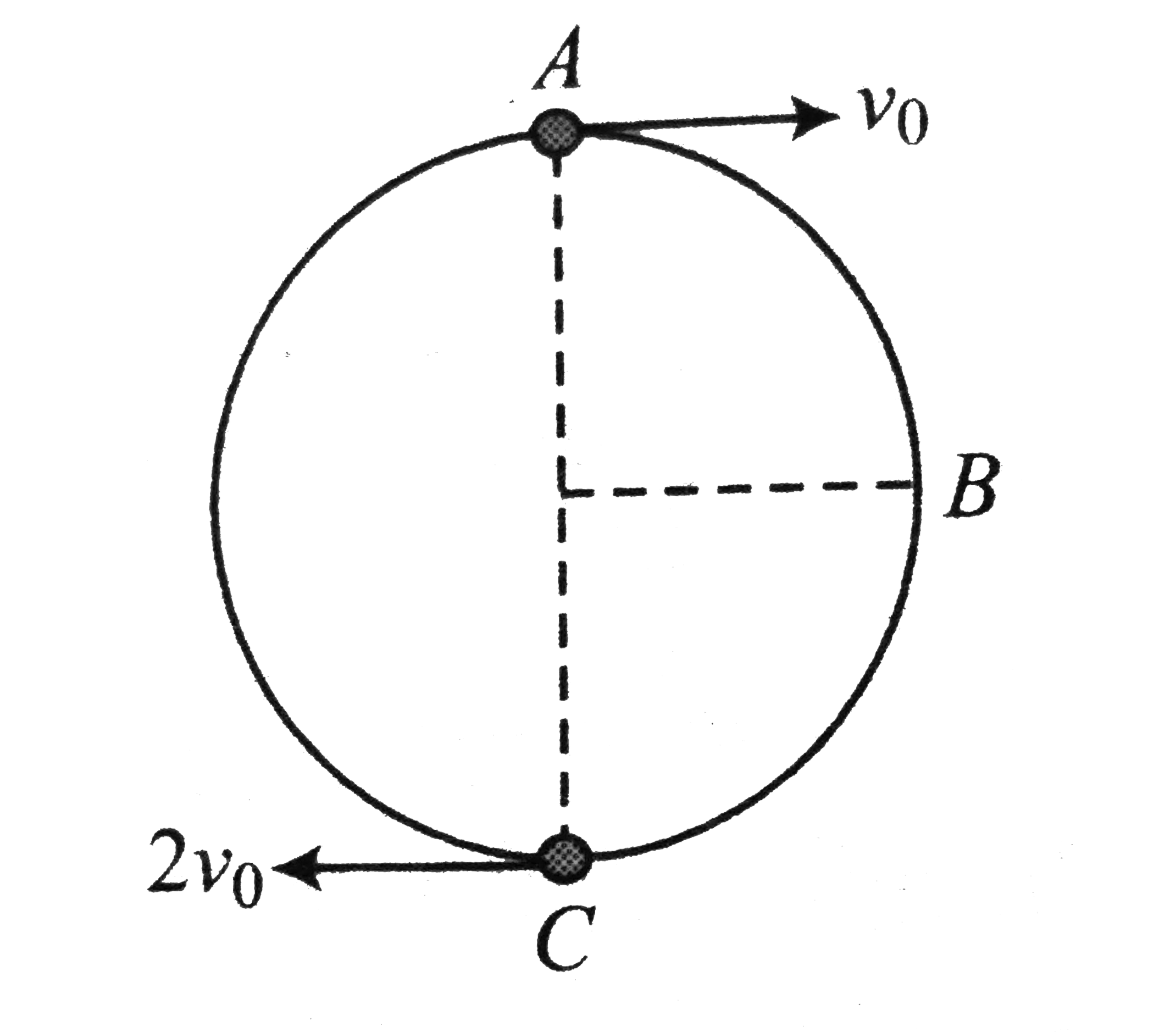
Let a ball of mass m be moving in a vertical circle of radius r, as shown in figure. Velocity of the ball is minimum when ball passes through highest point A and maximum when it passes through the lowest point C.
Let velocity of ball at A be $v_{0}$ then that at C will be equal to $2 v_{0}$ .

According to law of conservation of energy.
KE at C=KE at A + Loss of energy from A to C
$\frac{1}{2} m {(2 v_{0})}^{2} = \frac{1}{2} m v_{0}^{2} + m g (2 r)$
$v_{0}^{2} = \frac{4}{3} g r$
Velocity of the ball is directed vertically downward when the ball passes through B. Let velocity at this point be v. Then according to law of conservation of energy.
KE at B=KE at A+Loss of energy from A to B
$\frac{1}{2} m v^{2} = \frac{1}{2} m v_{0}^{2} + m g (r)$
$v^{2} = \frac{4}{3} g r + 2 g r = \frac{10}{3} g r$
Now considering FBD at B,
$T = \frac{m v^{2}}{r} = \frac{10}{3} m g$
$m g = m a_{1}$ or tangential acceleration, $a_{t} = g$
normal or centripetal acceleration.

$a_{n} = \frac{v^{2}}{r} = \frac{10}{3} g$
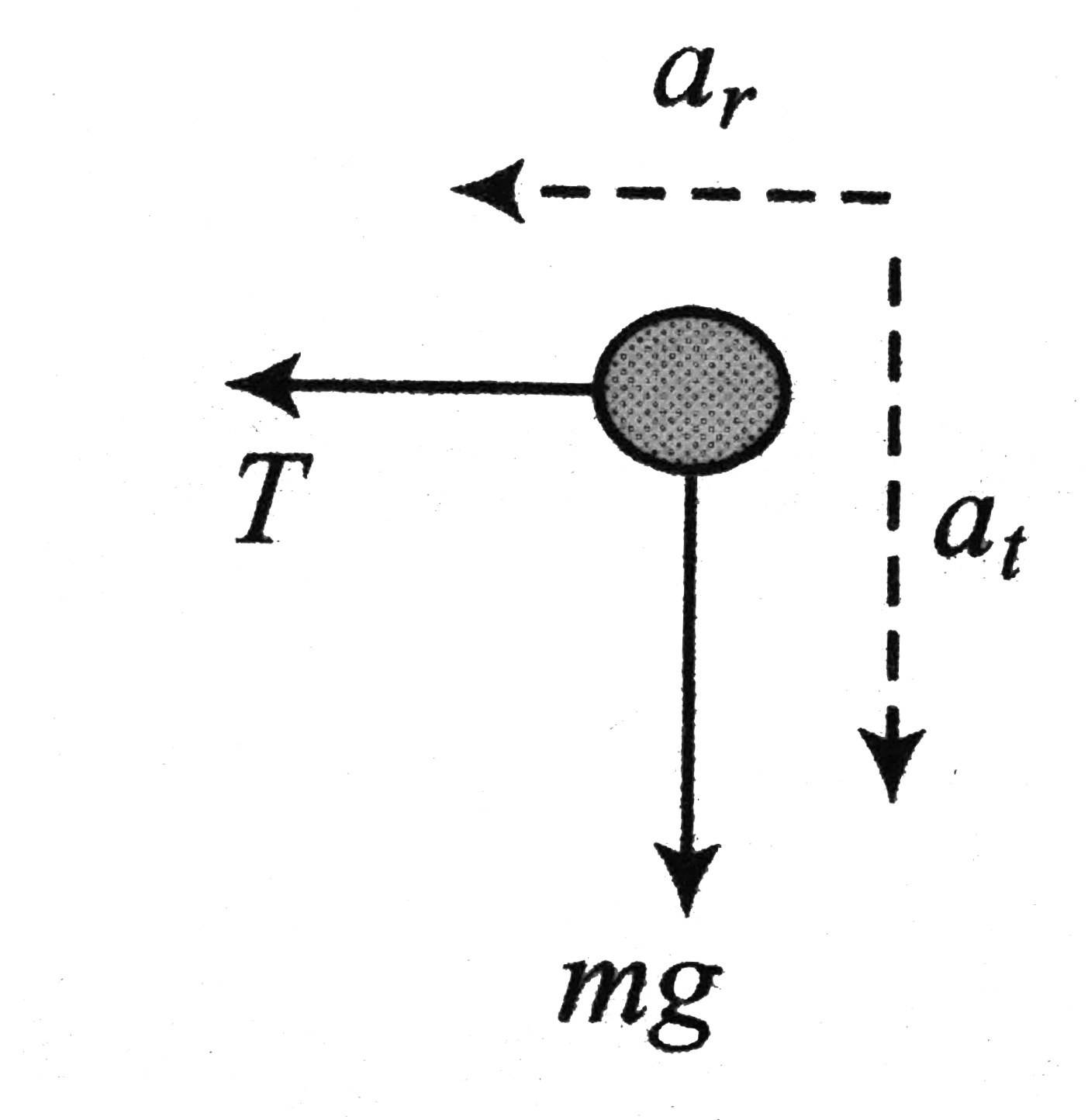
Net acceleration at ball of B will be equal to the vector sum of these two . ltbr> $a = \sqrt{a_{t}^{2} + a_{n}^{2}} = \frac{g}{3} \sqrt{109}$

Updated on:21/07/2023