A bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a dsitance.

L(1−cosθ)
(L2)(1−cosθ)
(L3)(1−cosθ)
(L6)(1−cosθ)
The correct Answer is:C
Let x= displacement of ring to the left
⇒Δxcm=2mx+m(x+L−Lcosθ)3m=0
⇒x=−13(1−cosθ)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle of mass m is attached to the celling of a cabin with an inextensible light string of length l. The cabin is moving upward with an acceleration a . The particle is taken to a position such that string makes an angle θ with vertical. When string becomes vertical, find the tension in the string.

View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
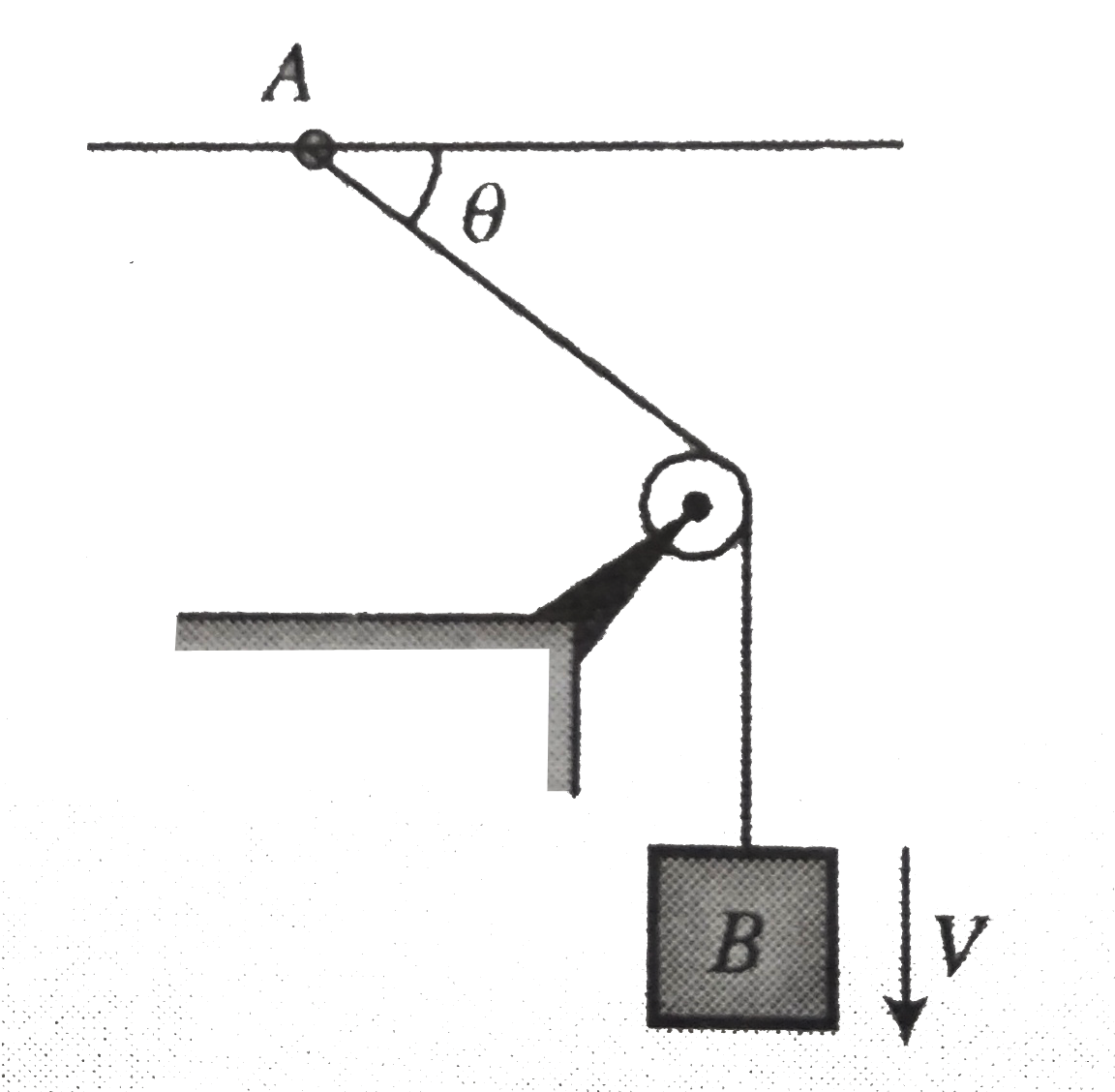
View Solution
Knowledge Check
A body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
Amu2lBmu2l+mgcosθCmu2l+mg(2cosθ−3)Dmu2l+mg(3cosθ−2)A particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√TmlA particle of mass m suspended by a string of length l revolves in a horizontal circle such that θ is the angle which the string makes with vertical. Which of the following statement (s) is/are correct ?
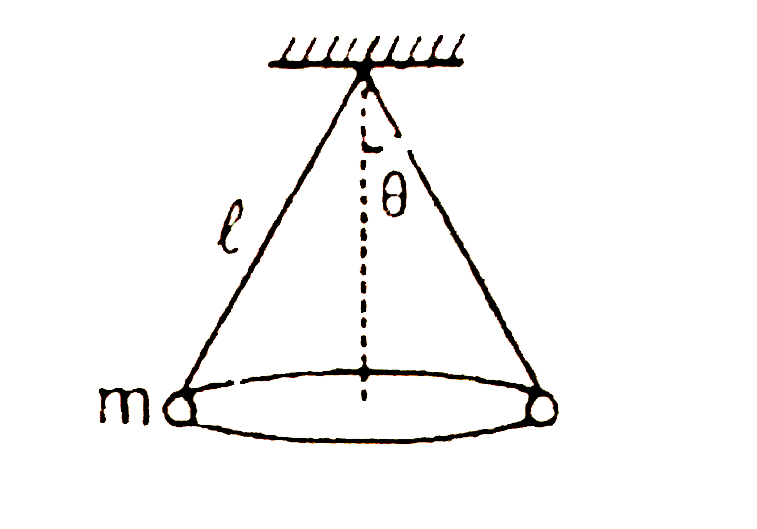 ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCTime period of revolution =2π√lcosθgDCentripetal acceleration =gtanθ
ATension in string =mgcosθBSpeed v of particle =√lgsin2θcosθCTime period of revolution =2π√lcosθgDCentripetal acceleration =gtanθ
" The force of attraction on a particle of mass "m" placed at the centre of curvature of a semicircular wire of length L and mass "M" is "
View SolutionA semicircular wire hs a length L and mass M. A paricle of mass m is placed at the centre of the circle. Find the gravitational attrction on the particle due to the wire.
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
View SolutionA bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
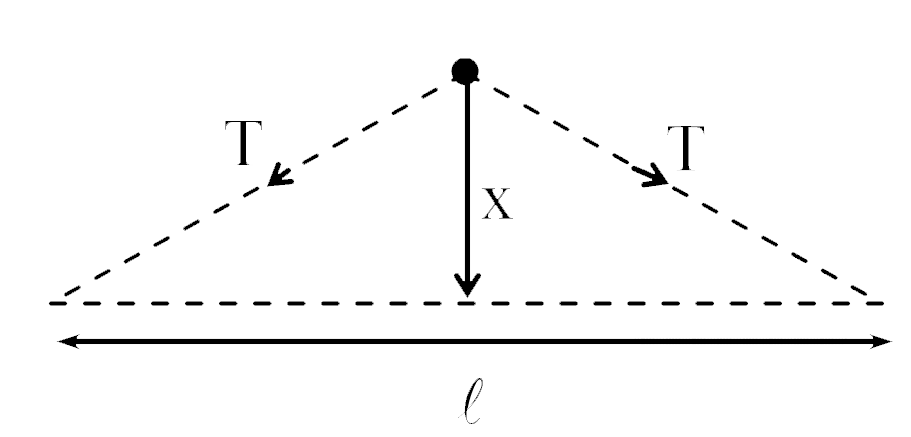
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-
View Solution
