A cubical tank carrying a non viscous liquid (water, moves down a smooth inclined plane. When we open the say) hole made at the mid-point P of the face of the tank, it strikes the point Q of the inclined plane. Find the of the tank at the time of opening the valve.

The correct Answer is:√ghcosθ
vrel=√2geffh2−√geffh=√ghcosθ
The actual velocity of the liquid v=(vr−v0)
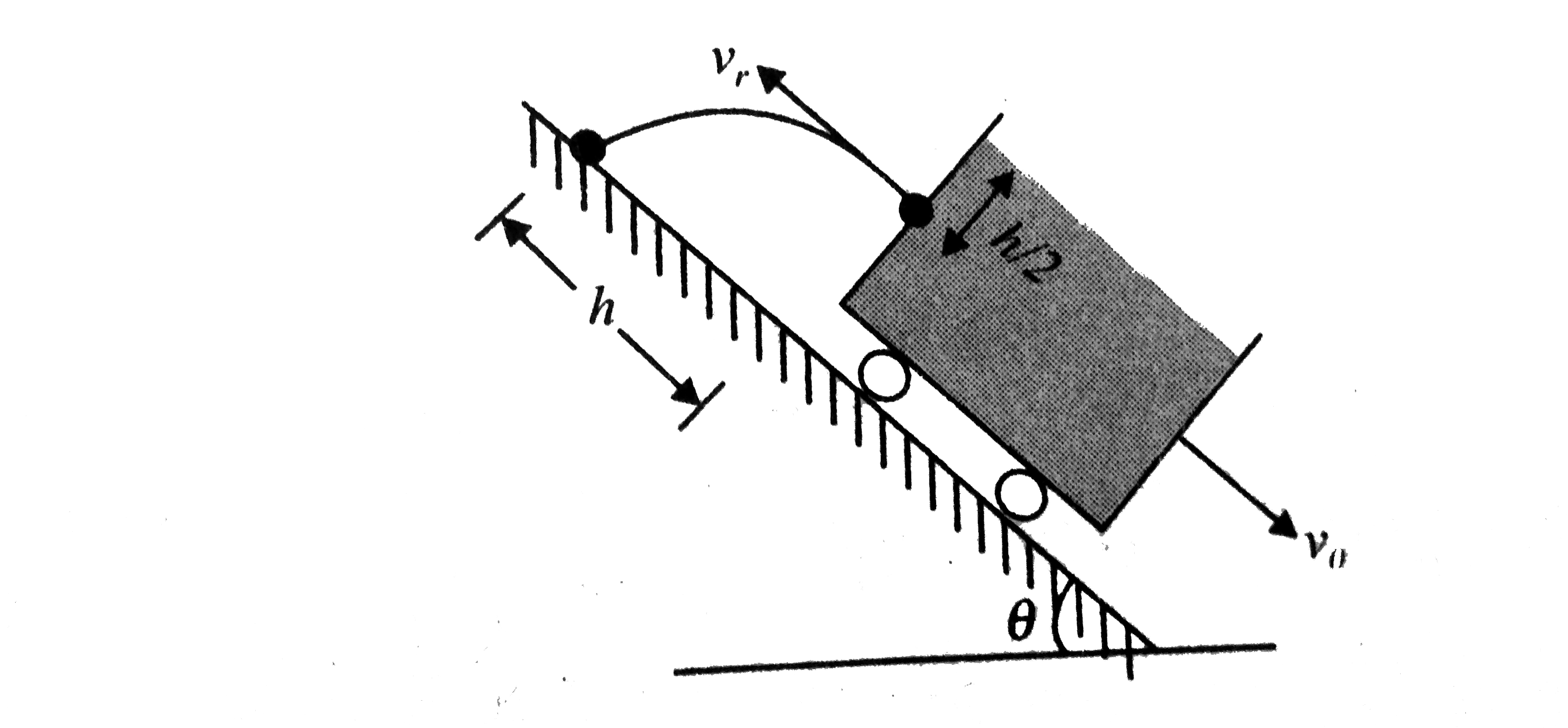
Then the time of flight T=
⎷2(h2)gcosθ=√hgcosθ
h=vt=12(gcosθ)T2 putting T,and v, we have
v0=h(1+tanθ2)√gcosθh+√ghcosθ
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A block sides down a smooth inclined plane when released from the top, while another falls freely from the same point. Which one of them will strike the ground : (a) earlier (b) with greater speed ?
View SolutionA ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
View Solution
Knowledge Check
A block slides down a smooth inclined plane when released from the top, while another falls freely from the same point :
Asliding block will reach the ground first with greater speedBfreely falling block will reach the ground first with greater speedCboth the blocks will reach the ground at the same time but with different speedsDboth the blocks will reach the ground with same speed but the freely falling block first
A ball falls freely form a height onto and smooth inclined plane forming an angle a with the horizontal. Find the ratio of the distance between the points at which the jumping ball strikes the inclined plane. Assume the impacts to be elastic.
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View SolutionA container containing a liquid is moving down an incline plane with constant acceleration 'a' . The angle made by the water surface in equilibrium with the inclined plane is

View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA rectangular box is sliding on a smooth inclined plane of inclination θ. At t=0 the box starts to move on the inclined plane. A bolt starts to fall from point A. Find the time after which bolt strikes the bottom surface of the box.
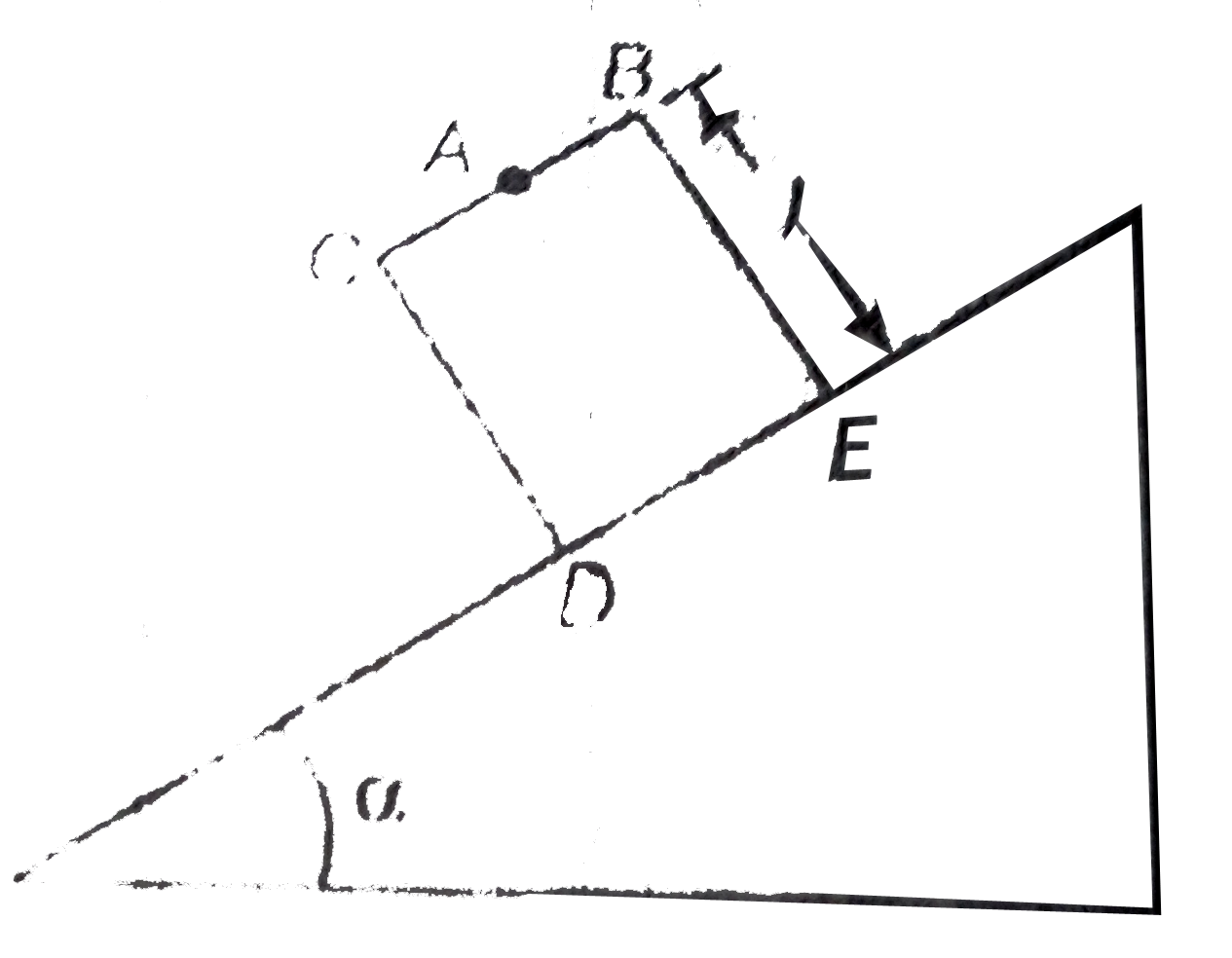
View Solution
