A wire of cross section is stretched horizontally between two clamps located apart. A weight is suspended from the mid-point of the wire. If the mid-point sags vertically through a distance the strain produced is
none of these
The correct Answer is:C
To solve the problem, we need to determine the strain produced in the wire when a weight is suspended from its midpoint, causing it to sag a certain distance.
1. Understanding the Setup:
- We have a wire of cross-sectional area A stretched horizontally between two clamps that are 2L meters apart.
- A weight W kg is suspended from the midpoint of the wire, causing it to sag vertically by a distance x.
2. Identifying the Lengths:
- The original length of the wire between the clamps is 2L.
- When the weight is applied, the wire sags downwards, creating two segments of the wire from the clamps to the weight. Each segment can be considered as a hypotenuse of a right triangle where:
- The horizontal leg is L (half of the total length).
- The vertical leg is x (the sag).
3. Calculating the New Length of the Wire:
- The length of each segment of the wire can be calculated using the Pythagorean theorem:
Length of each segment=√L2+x2
- Since there are two segments, the total length of the wire when the weight is applied is:
Total length=2×√L2+x2
4. Calculating the Change in Length:
- The change in length ΔL of the wire due to the sag is given by:
ΔL=Total length with weight−Original length
- Substituting the values:
ΔL=2√L2+x2−2L
5. Calculating the Strain:
- Strain is defined as the change in length divided by the original length:
Strain=ΔLOriginal length=2√L2+x2−2L2L
- Simplifying this gives:
Strain=√L2+x2−LL
6. Final Expression for Strain:
- Therefore, the strain produced in the wire is:
Strain=√L2+x2−LL
- We have a wire of cross-sectional area A stretched horizontally between two clamps that are 2L meters apart.
- A weight W kg is suspended from the midpoint of the wire, causing it to sag vertically by a distance x.
- The original length of the wire between the clamps is 2L.
- When the weight is applied, the wire sags downwards, creating two segments of the wire from the clamps to the weight. Each segment can be considered as a hypotenuse of a right triangle where:
- The horizontal leg is L (half of the total length).
- The vertical leg is x (the sag).
- The length of each segment of the wire can be calculated using the Pythagorean theorem:
Length of each segment=√L2+x2
- Since there are two segments, the total length of the wire when the weight is applied is:
Total length=2×√L2+x2
- The change in length ΔL of the wire due to the sag is given by:
ΔL=Total length with weight−Original length
- Substituting the values:
ΔL=2√L2+x2−2L
- Strain is defined as the change in length divided by the original length:
Strain=ΔLOriginal length=2√L2+x2−2L2L
- Simplifying this gives:
Strain=√L2+x2−LL
- Therefore, the strain produced in the wire is:
Strain=√L2+x2−LL
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Multiple Correct17videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Assertion- Reasoning13videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Subjective16videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
Similar Questions
A steel wire of diameter d=1.0mm is stretched horizontally between two clamps located at the distance l=2.0m from each other. A weight of mass m=0.25kg is suspended from the mid-point O of the wire. What will the resulting descent of the point O be in centrimetres?
View SolutionA steel wire of length 2L and cross-section area A is stretched, wetl within elastic limit horizontally between two pillars, a mass m is suspended from the mid-point of wire such that depression at the middle is X. Strain in the wire is proportional to
View Solution
Knowledge Check
- Question 1 - Select One
A mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
Ax22L2BxLCx2LDx22L - Question 2 - Select One
A mild steel wire of length 2L and cross-sectional area A is stretched, well within elastic limit, horizontally between two pillars,
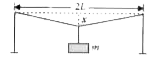
A mass m is suspended from the midpoint of the wire. Strain in the wire isAx22L2BxLCx2LDx22L - Question 3 - Select One
A mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
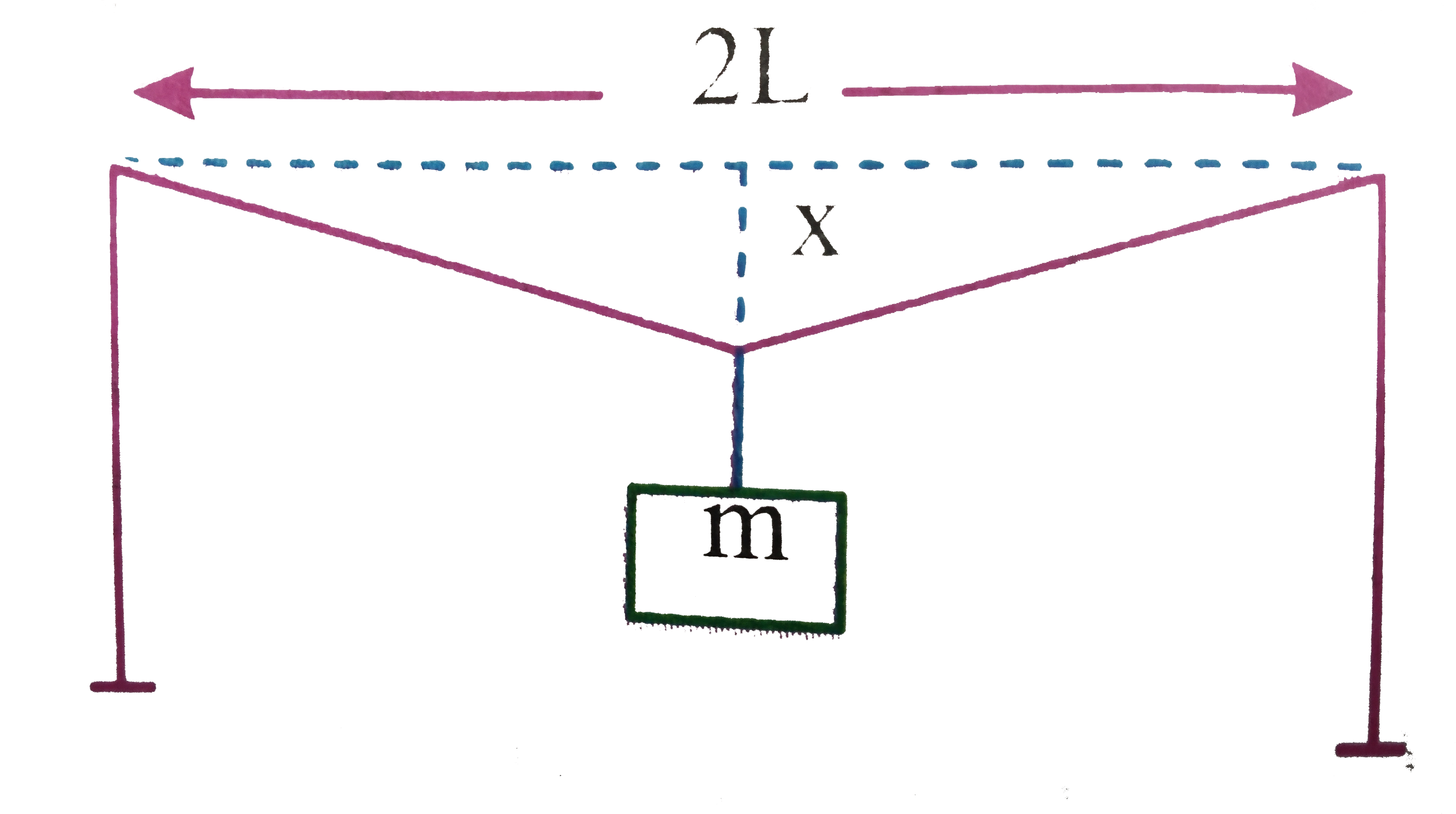 Ax22L2BxLCx2/LDx2/2L
Ax22L2BxLCx2/LDx2/2L
A mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View SolutionA mild steel wire of length 1.0 m and cross-sectional are 0.5×10−20cm2 is streached, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid point of the wire, calculate the depression at the mid point.
g=10ms−2,Y=2×1011Nm−2.
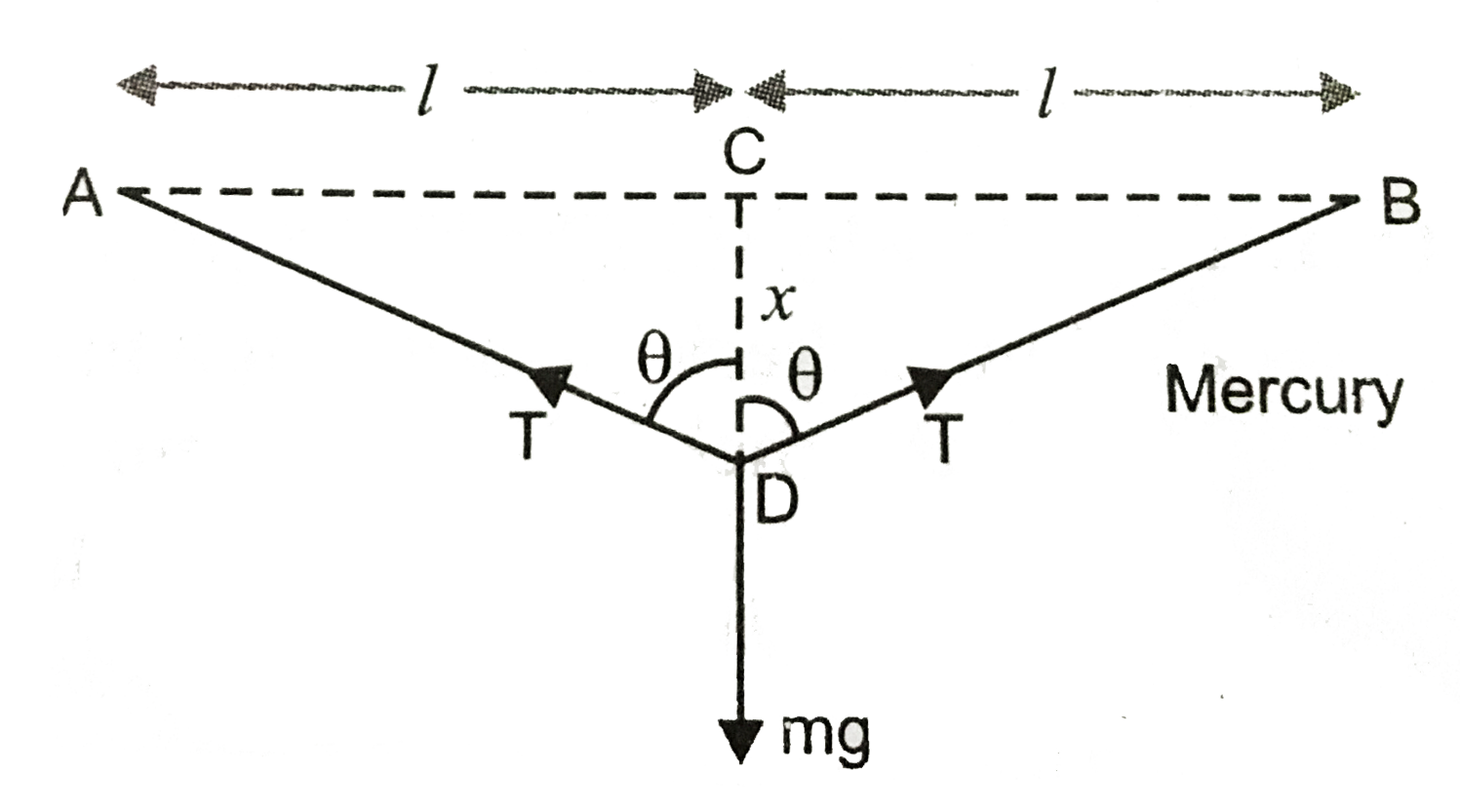 View Solution
View SolutionA steel wire of original length 1 m and cross-sectional area 4.00 mm^2 is clamped at the two ends so that it lies horizontally and without tension. If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ?
Yofthesteel=2.0x10^11Nm^-2. Take g=10ms−2View SolutionA steel wire of length 1m and diameter 4mm is stretched horizontally between two rigit supports attached to its end. What load would be required to be hung from the mid-point of the wire to produce a depression of 1cm? (Y=2×1011Nm−2)
View SolutionA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
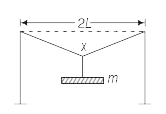 View Solution
View Solution

