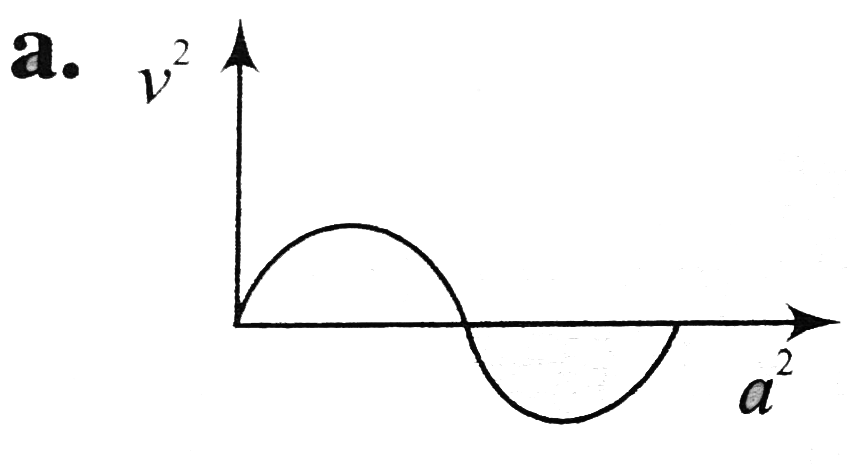
A graph of the square of the velocity against the square of the acceleration of a given simple harmonic motion is
A
B
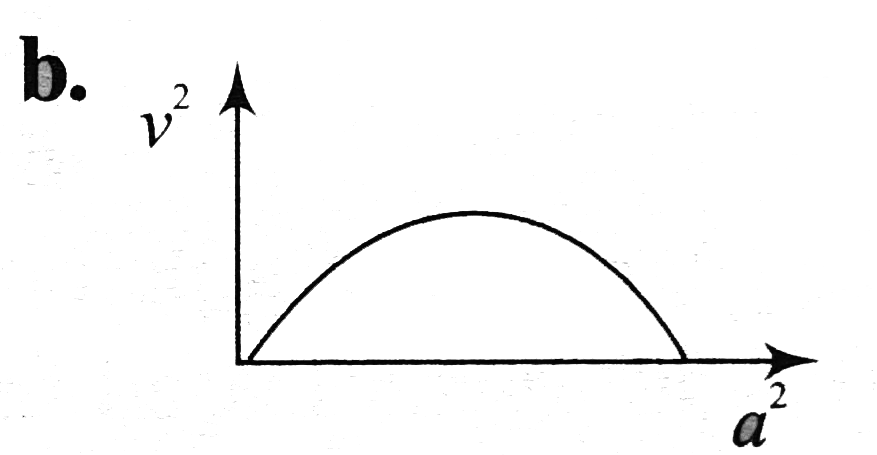
C
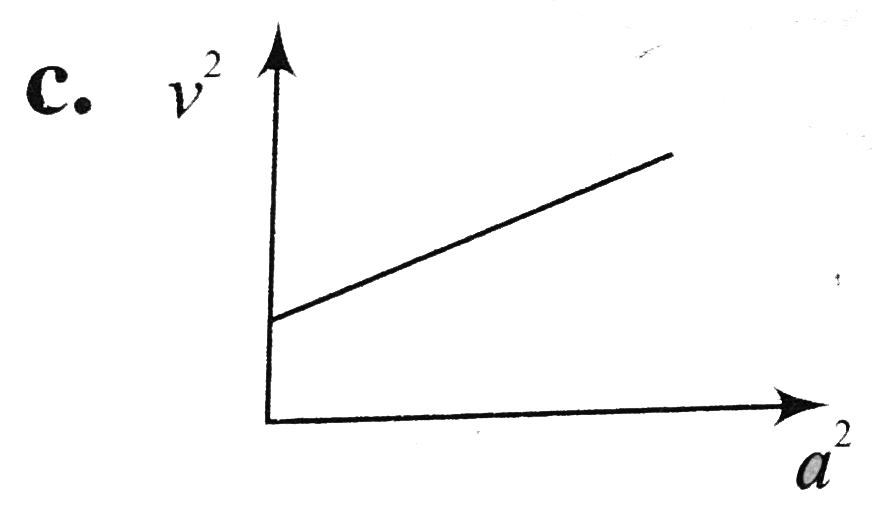
D
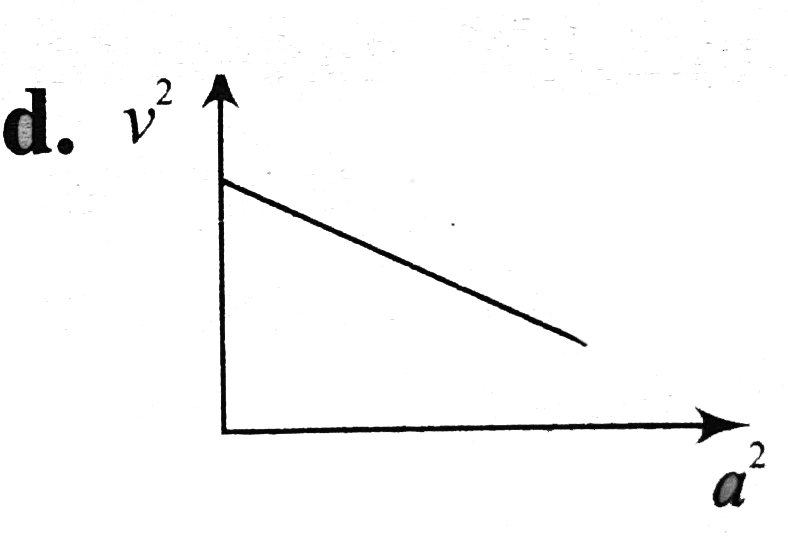
Video Solution
Text Solution
The correct Answer is:D
x=Asinωt
v=dxdt=Aωt=ω√A2−x2
a=dvdt=−Aω2sinωt
=dvdt=−ω2x
But x=−1ω2
v=ω√A2−a2ω4
or v2=ω2(A2−a2ω4)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning6videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective21videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
In simple harmonic motion
APotential energy and kinetic energy may not be equal in mean position.Bpotential energy and kinetic energy may be equal in extreme positionCpotential energy may be zero at extreme positionDkinetic energy plus potential energy oscillates simple harmonically. - Question 2 - Select One
In a simple harmonic motion
Athe potential energy is always equal to the kinetic energyBthe potential energy of is never equal to the kinetic energyCthe average potential energy in any time interval is equal to the average kinetic energy in that time intervalDthe average potential energy is one time period is equal to the averge energy is this period - Question 3 - Select One or More
In a simple harmonic motion
Athe maximum potential energy equals the maximum kinetic energyBthe minimum potential energy equals the minimum kinetic energyCthe minimum potential energy equals the maximum kinetic energyDthe maximum potential energy equals the minimum kinetic energy.
What is the direction of velocity in a simple harmonic motion ?
View SolutionThe equation of motion of a simple harmonic motion is
View SolutionThe equation of motion of a simple harmonic motion is
View SolutionThe average acceleration in one tiome period in a simple harmonic motion is
View SolutionThe velocity of a particle executing simple harmonic motion is
View Solution
