One end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate
(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.
3 cm
20 cm
10 cm
100 cm
The correct Answer is:A
Conserving linear momentum
(1+3)v=1×0.3+3(−0.3)
v=−0.15ms
Negative sign indicates that combined body starts to move leftwards. But at the instant of collision, spring is in its natural length or combined by is in equilibrium position. Hence at t=0, phase of combinied body becomes equal to π.
Therefore new amplitude of oscillaion is
a'=|a|ω=0.155=0.03m=3cm
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass 0.1 kg attached to a spring of spring constant 400 N/m is pulled rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View Solution
Knowledge Check
A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
Athe block will perform SHM of amplitude 5cmBthe block will have maximum velocity 30√5cm/sCthe block will have maximum acceleration 15m/s2Dthe minimum elastic potential energy of the spring will be zeroA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv)a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2J
One end of a spring is rigidly fixed. A block attached to the free end of the spring is pulled through a distance x0. On releasing the block, its amplitude of motion cannot exceed ±x0. Why?
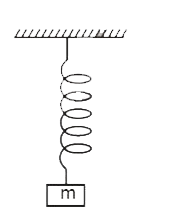
View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.

View SolutionAn ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View Solution
