A body is at rest at x=0 . At t=0, it starts moving in the positive x−direction with a constant acceleration . At the same instant another body passes through x=0 moving in the positive x−direction with a constant speed . The position of the first body is given by x1(t) after time 't', and that of the second body by x2(t) after the same time interval . which of the following graphs correctly describes (x1−x2) as a function of time 't' ?
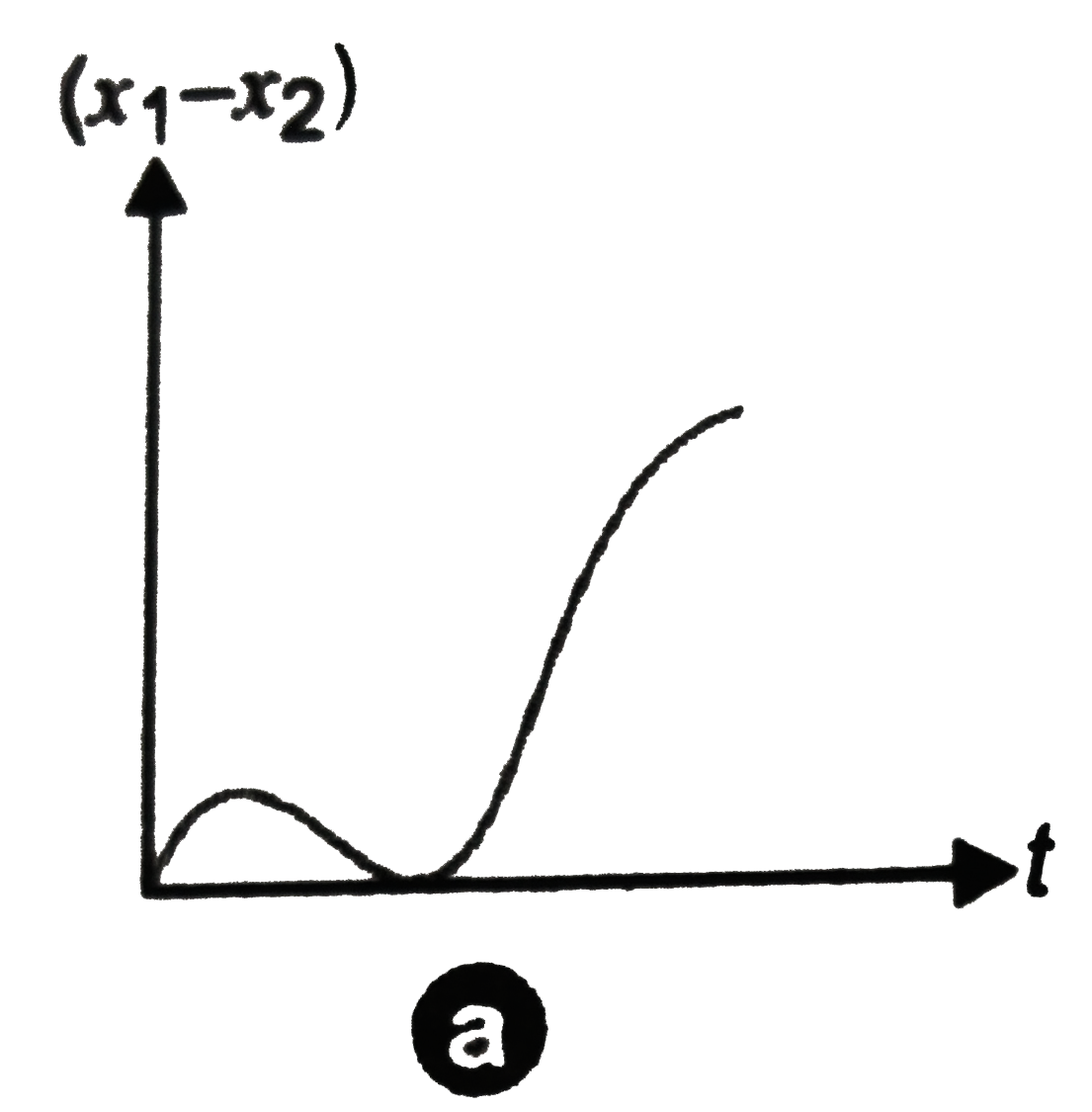
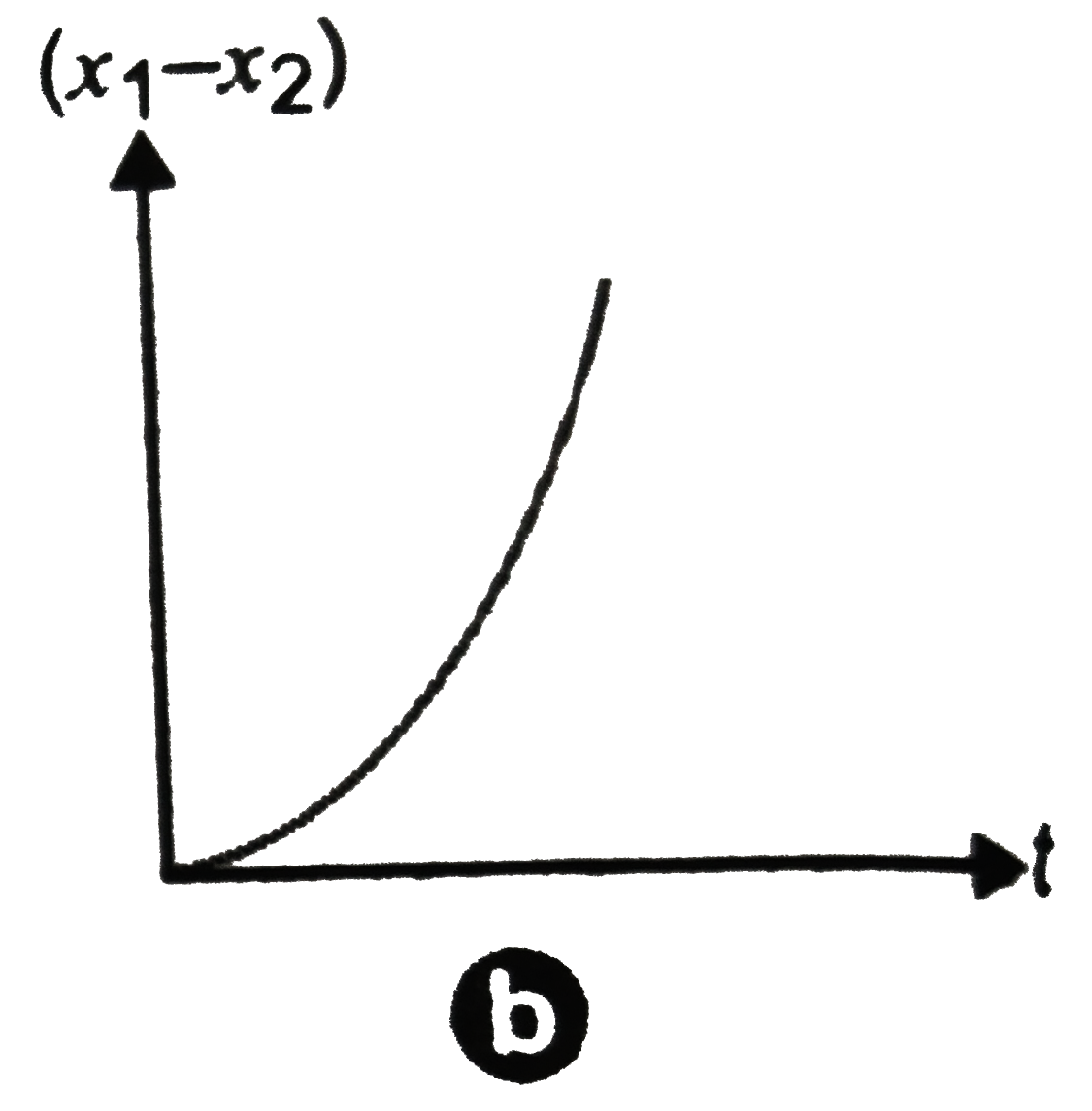
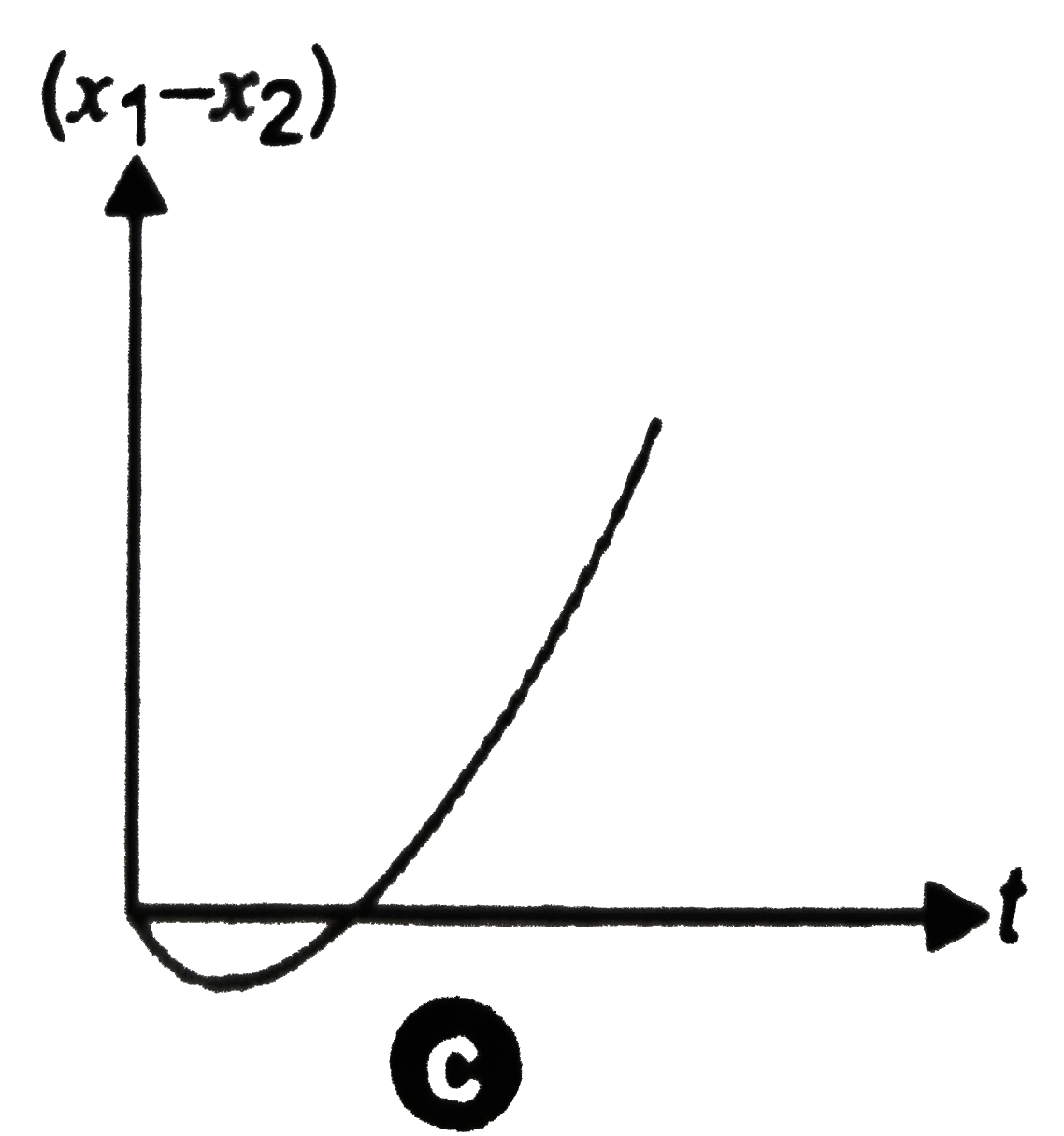

The correct Answer is:C
As u=0, for body 1,v1=at and for bodt 2,v2=a constant. Initially both are at x=0. Relative velocity of body 1 w.r.t. body 2=→−1−→–––2. At first, the velocity v1 is less than →–––2. The distance travelled by body 1 i.e. x-1 = 1/2 at^2 - v_2 t. This shows that the graph between 9x_1 -x_2) and (t) is a parabola before crossing (x0 axis as well as after crossing x-axis. the curve (c ) satisfies this.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 NCERT multiple Choice
10 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 NCERT Integer type
4 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 NCERT multiple
15 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
A body A moves with a uniform acceleration a and zero initial velocity. Another body B, starts from the same point moves in the same direction with a constant velocity v. The two bodies meet after a time t. The value of t is
View SolutionA particle starts moving from position of rest under a constant acceleration if it travels a distance x in t second, what distance will it travel in next t second?
View Solution
Knowledge Check
A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=p√x. The displacement of the particle varies with time as (where, p is constant)
At3Bt2CtDt1/2A particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
At2BtCt12Dt3A wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given byAg(x,t)=Asin[x−v(t−t0)]2a2Bg(x,t)=Asin[x+v(t−t0)]2a2Cg(x,t)=Asin[x−v(t+t0)]2a2Dg(x,t)=Asin[x+v(t+t0)]2a2
A particle located at position x=0, at time t=0, starts moving along the positive x-direction with a velocity v2=αx (where alpha is a positive constant). The displacement of particle is proportional to
View SolutionA particle starts moving from the position of rest under a constant acc. If it travels a distance x in t sec, what distance will it travel in next t sec ?
View SolutionA particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View SolutionA particle located at "x=0" at time "t=0" starts moving along the positive "x" - direction with a velocity "v" that varies as "v=alpha sqrt(x)".The displacement "(x)" of the particle varies with time as "(alpha" is constant)
View SolutionThe displacement to particle is zero at t=0andiszatt=t. It starts moving in the positive x-direction with a velocity which varies, v=k√x, wher (k) is a constant. Find the relation for variation of velocity with time.
View Solution