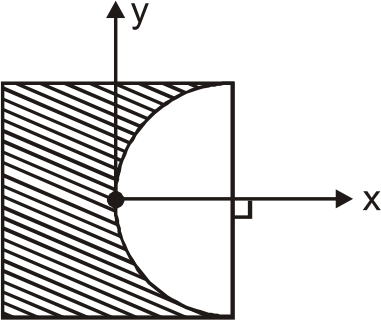
In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
A
−π(π−2)l2(8−π)
B
π(π−2)l2(8−π)
C
−π(π−2)l8−π
D
−l(π−43)2(8−π)
Video Solution
Text Solution
xcm=m1x1+m2x2m1+m2
m1=mass of square plate
=m
x1=c.m. of square plate =0
m2 =mass of removed part
=−ml2⎛⎜⎝πl242⎞⎟⎠=−π8m
x2=c.m. of removed part
=l2−43π(l2)=l2(1−43π)
∴xcm=−πm8.l2(1−43π)m−π8m,xcm=−l(π−43)2(8−π)
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the x coordinate of the centre of mass of the bricks shown in figure :
 A2425lB2524lC1516lD1615
A2425lB2524lC1516lD1615 - Question 2 - Select One
From a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
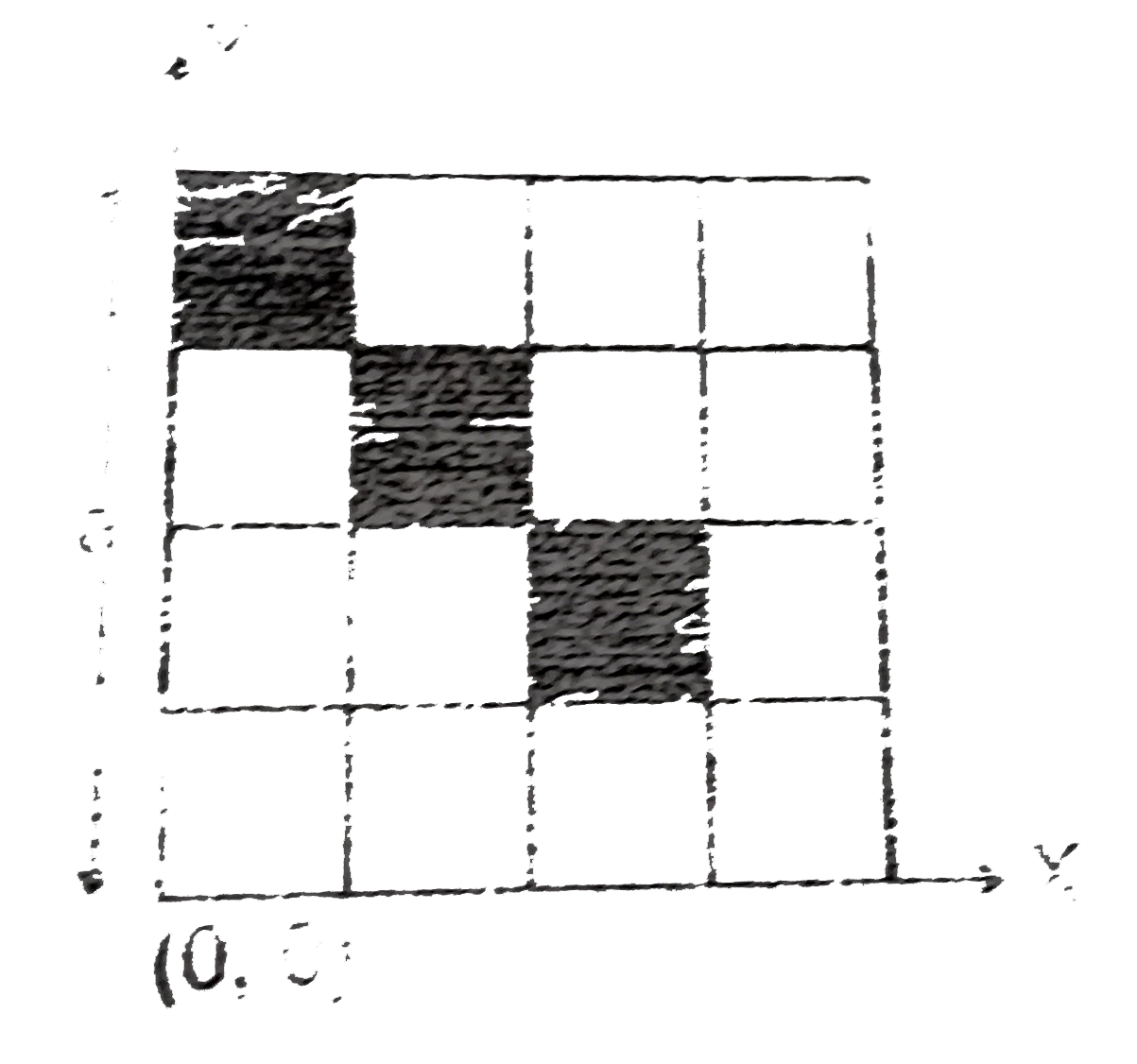 Ax<a2,y<a2Bx>a2,y<a2Cx<a2,y>a2Dx>a2,y>a2
Ax<a2,y<a2Bx>a2,y<a2Cx<a2,y>a2Dx>a2,y>a2 - Question 3 - Select One

From a uniform square plate of side a and mass m, a square portion DEFG of side a2 is removed. Then, the moment of inertia of remaining portion about the axis AB isA7ma216B3ma216C3ma24D9ma216
The coordinate of the centre of mass of a system as shown in figure : -
 View Solution
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
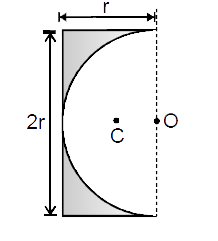 View Solution
View SolutionThe centre of mass of a triangle shown in figure has coordinates
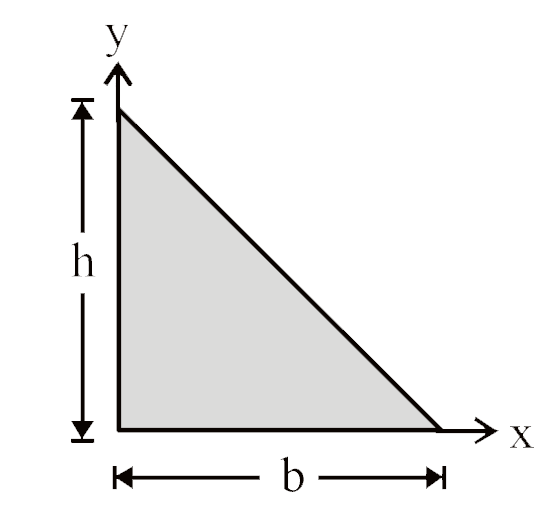 View Solution
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.
 View Solution
View SolutionFigure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
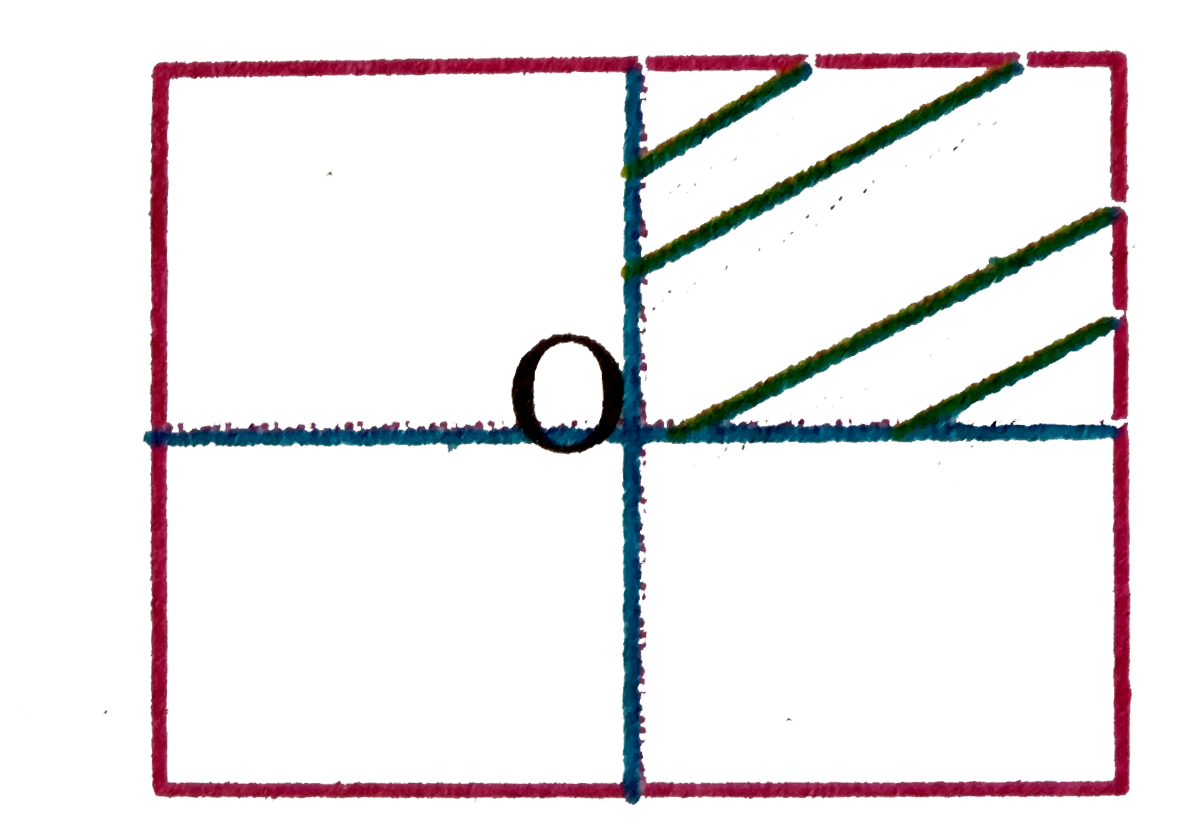 View Solution
View Solution