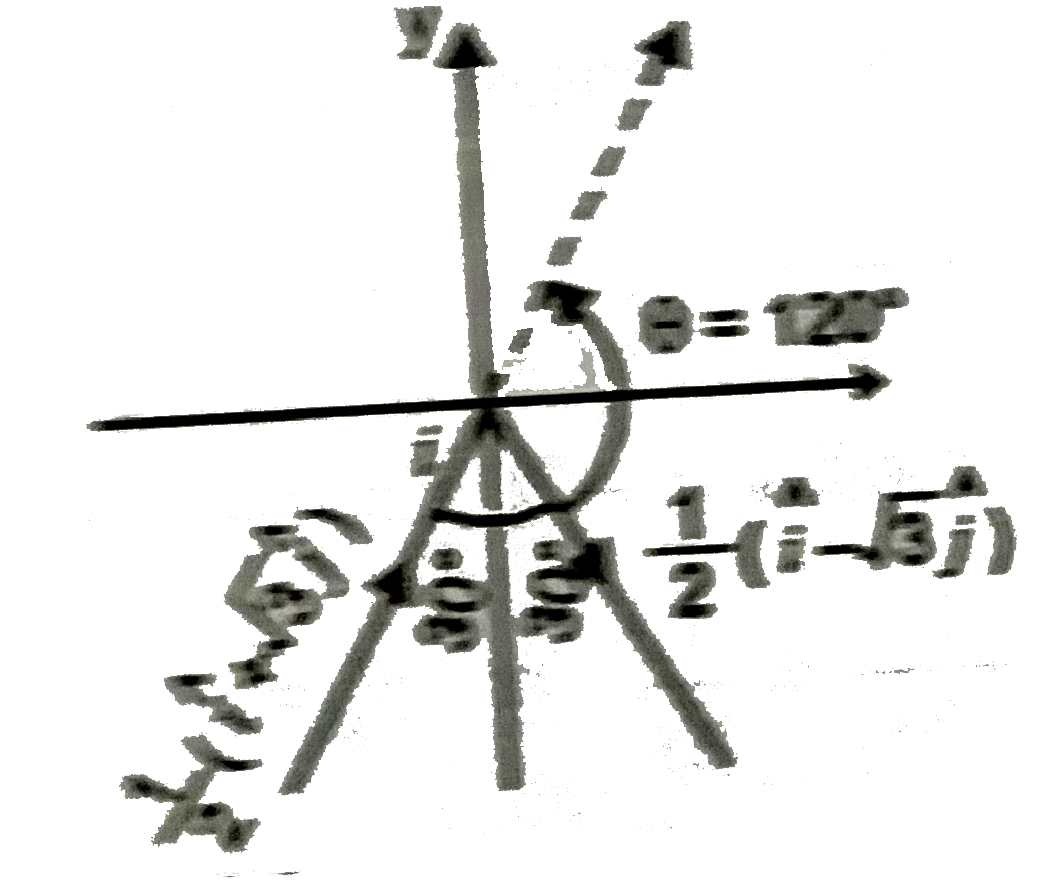
A ray of light travelling in the direction $\frac{1}{2} (ˆ i + \sqrt{3} ˆ j)$ is incident on a plane mirror. After reflection, it travels along the direction $\frac{1}{2} (ˆ i - \sqrt{3} ˆ j)$ . The anglel of incidence is

A

$30^{\circ}$

B

$45^{\circ}$

C

$60^{\circ}$

D

$75^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Here, $\to A = \frac{1}{2} (ˆ i + \sqrt{3} ˆ j)$
and $\to B = \frac{1}{2} (ˆ i - \sqrt{3} ˆ j)$
$∴ A = B = \sqrt{I^{2} + {(\sqrt{3})}^{2}} = 2$ and $\to A . \to B = - 2$
$cos θ = \frac{\to A . \to B}{A B} = \frac{- 2}{2 \times 2} = - \frac{1}{2}$
$θ = 120^{\circ}$ , Fig.
Angle of incidence,
$i = \frac{180^{\circ} - θ}{2} = \frac{180^{\circ} - 120^{\circ}}{2} = 30^{\circ}$ .
.

|

Updated on:21/07/2023

Class 11 PHYSICS RAY OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ray of light travelling in the direction $\frac{1}{2}$ $(ˆ i, + \sqrt{3} ˆ j)$ is incident on a plane mirror. After reflection, it travels along the direction (1)/(2)(hati-sqrt3hatj) . The angle of incidence is
A30degree
B60degree
C45degree
D75degree
Question 2 - Select One
A ray of light travelling in the direction $\frac{1}{2} (ˆ i + \sqrt{3} ˆ j)$ is incident on a plane mirror. After reflectiion, it travels along the direction $\frac{1}{2} (ˆ i + \sqrt{3} ˆ j)$ . The angle of incidence is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$
Question 3 - Select One
The expression $(\frac{1}{\sqrt{2}} ˆ i + \frac{1}{\sqrt{2}} ˆ j)$ is a
AUnit vector
BNull vector
CVector of magnitude sqrt(2)
DScalar

PRADEEP-RAY OPTICS-(Competition)Multiple choice

Home
Ask Doubt
Profile