Find the magnetic field B at the center of a rectangular loop of length l and width b, carrying a current i.
The correct Answer is:2μ0I√a2+b2πab
Let →B1,→B2,→B3 and →B4 be the magnetic field at O due to current in arms 1,2,3 and 4 respectively, figue.
The total magnetic field induction at O due to current through rectangular loop is
→B=→B1+→B2+→B3+→B4
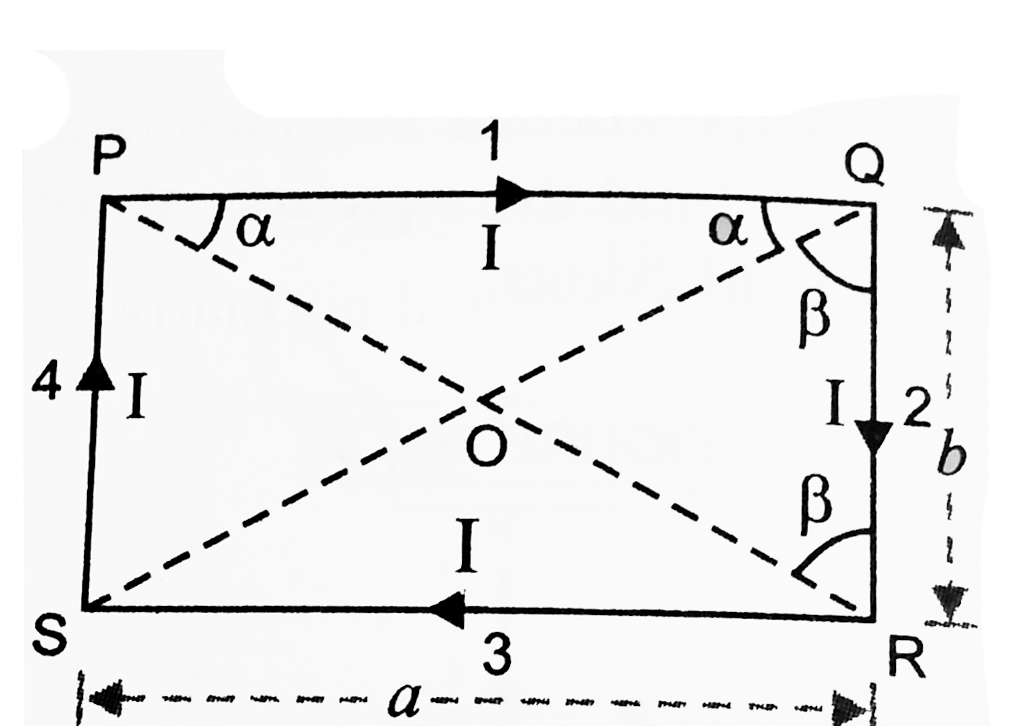
where, B1=B3=μ04πI(b/2)
×[sin(90∘−α)+sin(90∘−α)]
=μ04π2Ib[cosα+cosα]
=μ04π2Ib×2cosα=μ0πIb×a√a2+b2
and B2=B4=μ04πI(a/2)
×[sin(90∘−β)+sin(90∘−β)]
=μ04π2Ia[cosβ+cosβ]
μ04π2Ia2cosβ=μ0πIab√a2+b2
As →B1,→B2,→B3 and →B4 are acting in the same direction, i.e., perpendicular to the plane of rectangular loop downwards.
∴B=B1+B2+B3+B4
=μ0πI√a2+b2[ab+ba+ab+ba]
=μ0π2I√a2+b2[ab+ba]
=μ0π2I√a2+b2ab
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (a)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Test Your Grip (c)1videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Value Based Questions2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions1videos
OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
A9μ0i4πLB3√3μ0i4πLC2√3μ0iπLD3μ0i4πL - Question 2 - Select One
The magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπL - Question 3 - Select One
The magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπL
(a) State Bio-Savart's law in vector form expressing the magnetic field due to an element →dl carrying current I at a distance r from the element.
(b) Write the expression for the magnitude of the magnetic field at the centre of a circular loop of radius 'R' carrying a steady current I. Draw the field lines due to the current loop.View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionThe magnetic field B within the solenoid having n turns per unit length and carrying a current I is given by
View SolutionMagnetic induction produced at the center of a circular loop of radius R carrying a current is 'B' The magnetic moment of the loop is
View SolutionThe magnetic field B with in the solenoid having n turns per metre length and carrying a current of i ampere is given by
View Solution

