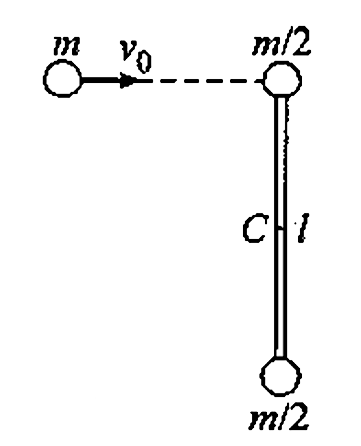
A ball of mass m moving with velocity v0 experiences a head-on elastic collision with one of the spheres of a stationary rigid dumbbell as whown in figure. The mass of each sphere equals m/2, and the distance between them is l. Disregarding the size of the spheres, find the proper angular momentum ˜M of the dumbbell after the collision, i.e. the angular momentum in the reference frame moving translationally and fixed to the dumbbell's centre of inertia.

From conservation of linear momentum along the direction of incident ball for the system consists with colliding ball and phhere
mv0=mv′+m2v1 (1)
where v′ and v1 are the velocities of ball and sphere 1 respectively after collision. (Remember that the collision is head on).
As the collision is perfectly elastic, from the definition of co-efficient of restitution,
1=v′−v10−v0 or, v′−v1=−v0 (2)
Solving (1) and (2), we get,
v1=4v03, directed towards right.
In the C.M. frame of spheres 1 and 2 (figure)
˜→p1=−˜→p2 and ∣∣˜→p1∣∣=∣∣˜→p2∣∣=μ|→v1−→v2|
Also, →r1C=−→r2C, thus ˜→M=2[l2m/224v03ˆn]
(where ˆn is the unit vector in the sense of →r1Cט→p1)
Hence ˜M=mv0l3

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A ball ofmass m moving with velocity experiences a head on elastic collision with one of the spheres of as tationary rigid dumbbell as shown in figure-5.149. The mass of each sphere equals m/2, and the distance between them is l.Disregarding the size of the spheres, find the angular momentum of the dumbbell in the reference frame moving translationally and fixed to the centre of mass of the dumbbell.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A30∘B60∘C120∘D90∘A ball of mass m moving with velocity V, makes a head on elastic collision with a ball of the same moving with velocity 2V towards it. Taking direction of V as positive velocities of the two balls after collision are.
A−Vand2VB2Vand−VCVand−2VD−2vandVA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
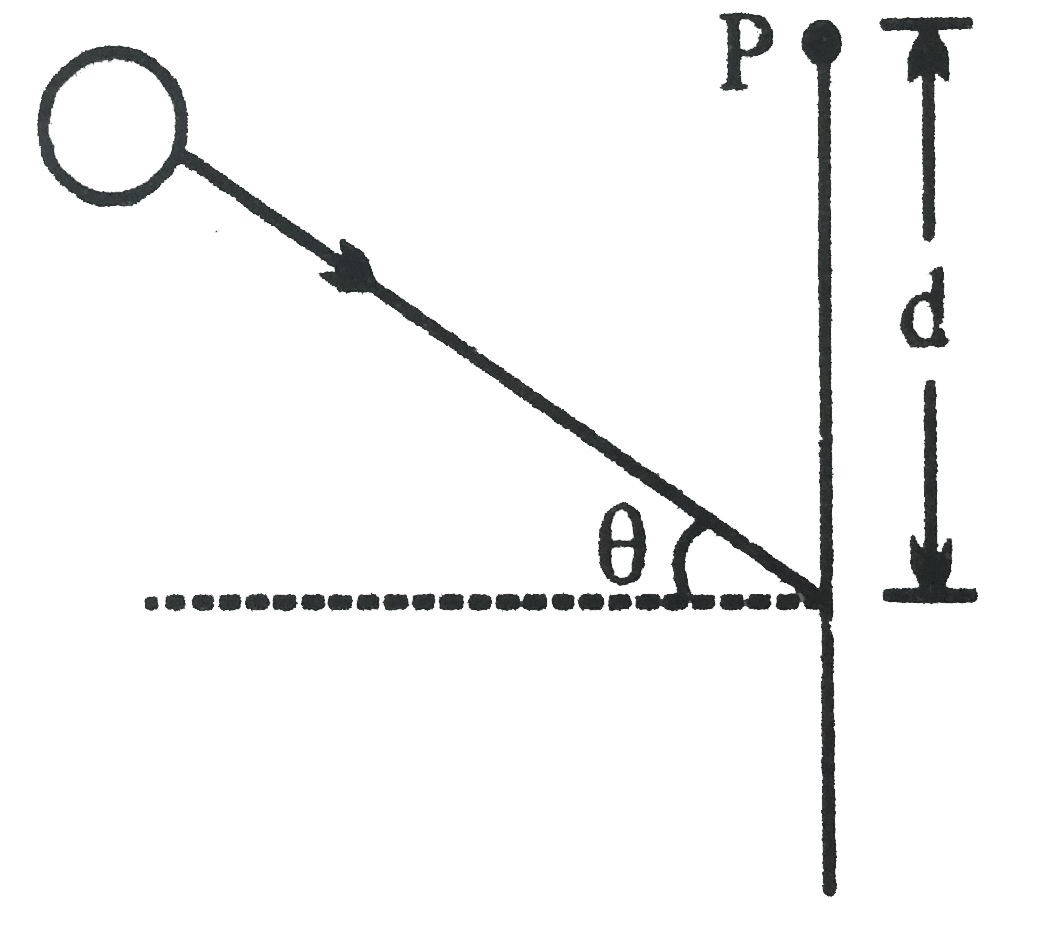 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzero
A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
 .
.
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionWhen two spheres of equal masses undergo glancing elastic collision with one of them at rest after collision they will move
View Solution
