Two small identical discs, each of mass m, lie on a smooth horizontal plane. The discs are interconnected by a light non-deformed spring of length l0 and stiffness ϰ. At a certain moment one of the disc is set in motion in a horizontal direction perpendicular to the spring with velocity v0. Find the maximum elongation of the spring in the process of motion, if it is known to be considerably less than unity.
In the C.M. frame of the system (both the discs+spring), the linear momentum of the discs are related by the relation, ˜→p1=−˜→p2, at all the moments of time.
where, ˜p1=˜p2=˜p=μvrel
And the total kinetic energy of the system,
T=12μv2_(rel)
Bearing in mind that at the moment of maximum deformation of the spring, the projection of →vrel along the length of the spring becomes zero, i.e vrel(x)=0.
The conservation of mechanical energy of the considered system in the C.M. frame gives.
12(m2)v20=12kx2+12(m2)v2rel(y) (1)
Now from the conservation of angular momentum of the system about the C.M.,
12(l02)(m2v0)=2(l0+x2)m2vrel(y)
or, vrel(y)=v0l0(l0+x)=v0(1+xl0)−1≈v0(1−xl0), as x<<l0 (2)
Using (2) in (1), 12mv20[1−(1−xl0)2]=kx2
or, 12mv20⎡⎣1−(1−2xl0+x2l20)2⎤⎦=kx2
or, mv20xl0≈kx2, [neglecting x2/l20]
As x≠0, thus x=mv20kl0
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body56videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics59videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
Two identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
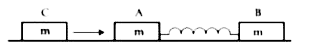 View Solution
View SolutionA block of mass m fitted with a light spring of stiffness k and natural length l0 kept on a smooth radial groove made on a disc rotaing with a constant angular axis . If the block is released slowly . Find the maximum elongation of the spring
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical particle each of mass m are inter connects by a light spring of stiffness k ,the time period for small oscillation is equal to
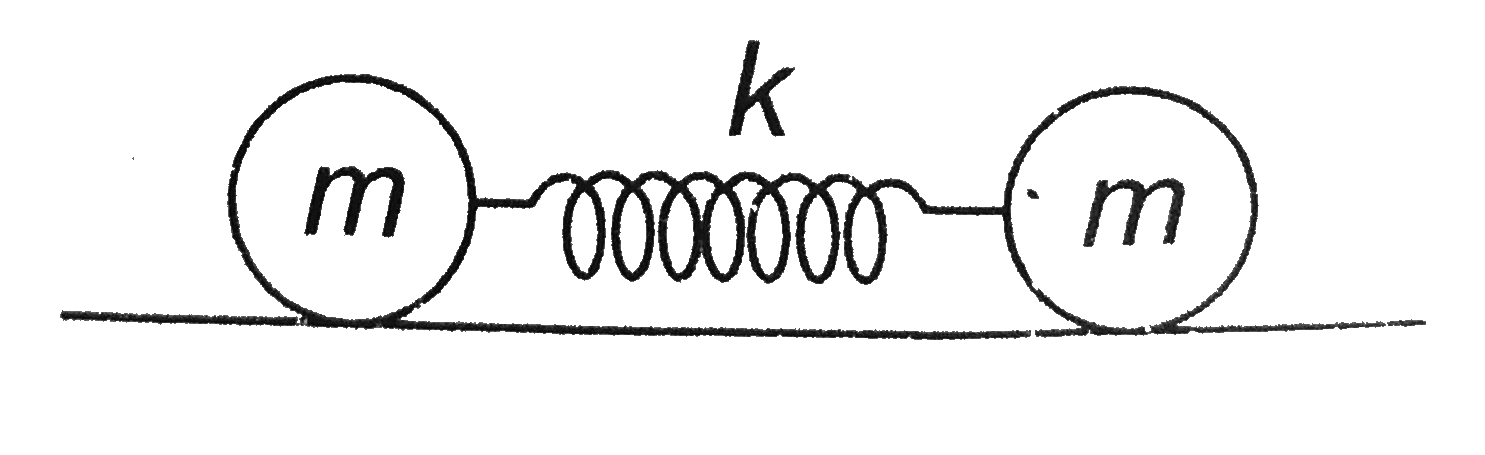 A2π√mkBπ2√mkCπ√m2kDπ√2mk
A2π√mkBπ2√mkCπ√m2kDπ√2mk - Question 2 - Select One
Two identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
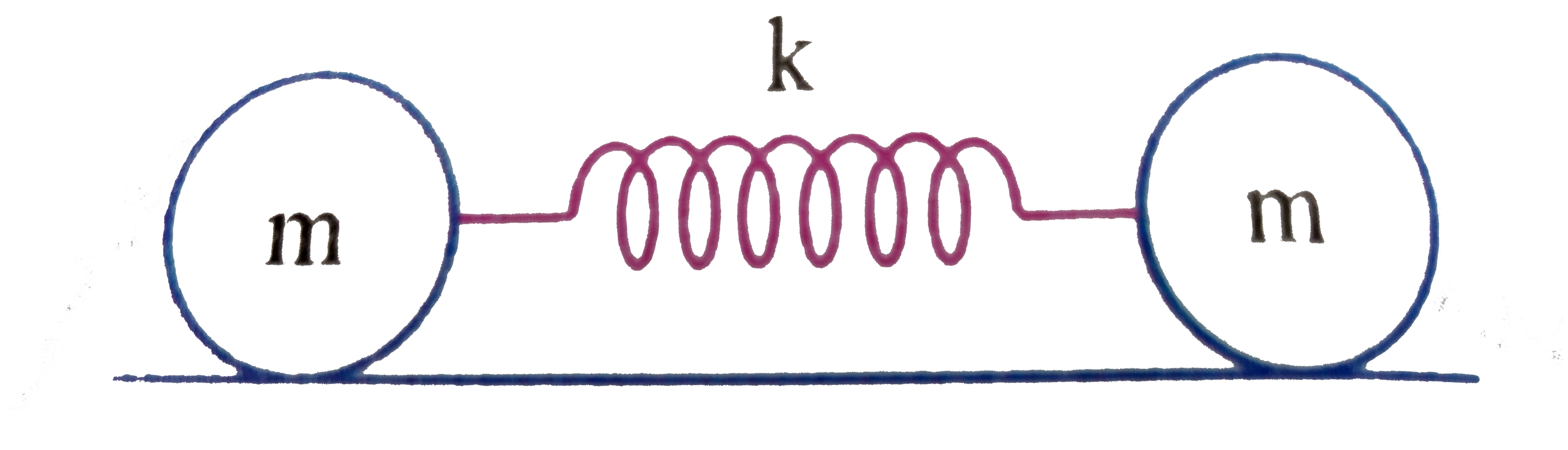 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10s
A block of mass m fitted with a light spring of stiffness k and natural length l0 kept on a smooth radial groove made on a disc rotaing with a constant angular axis . If the block is released slowly . Find the maximum elongation of the spring
 View Solution
View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.
 View Solution
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
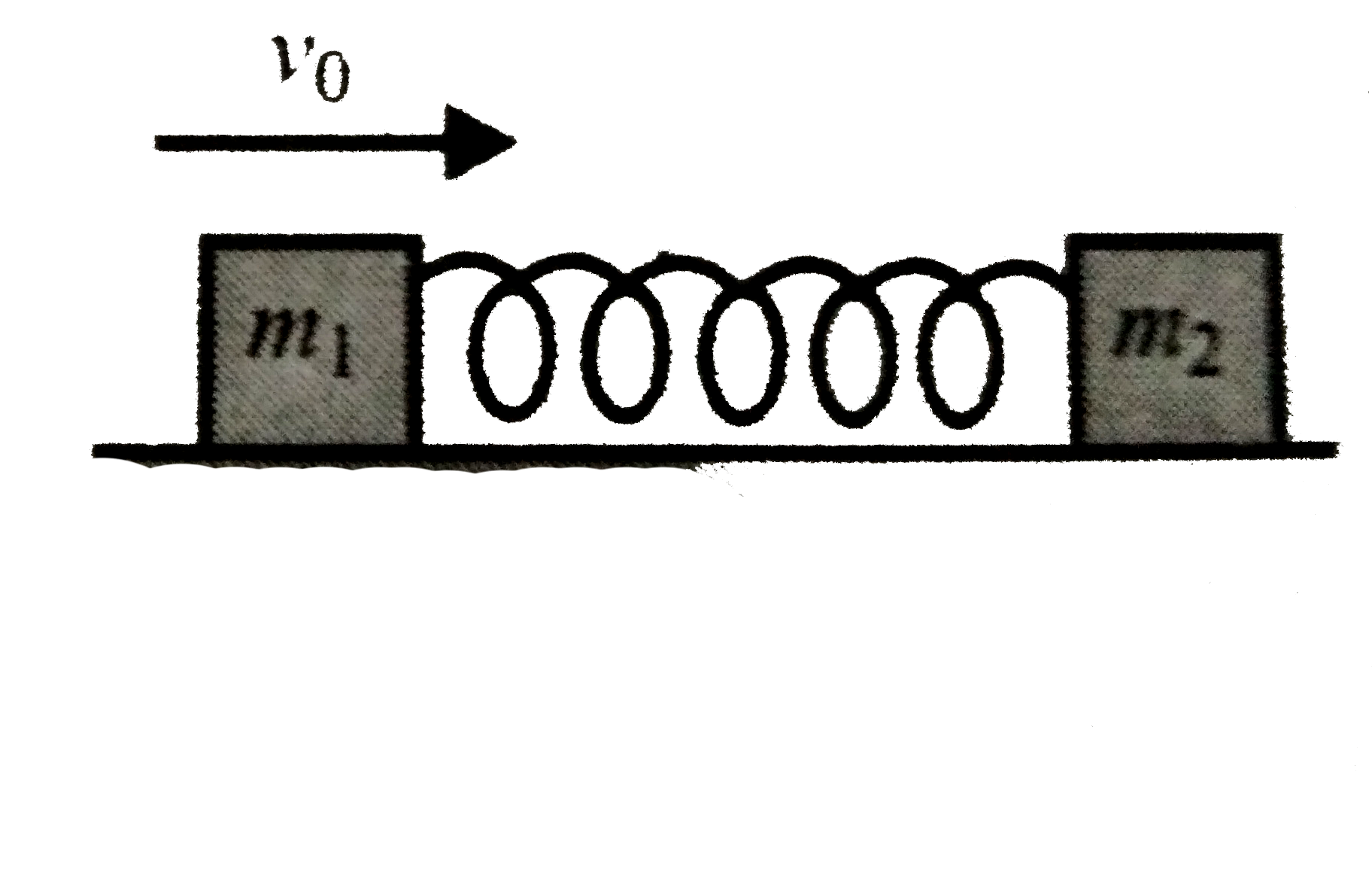 View Solution
View SolutionTwo smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
 View Solution
View SolutionTwo small discs of masses m1 and m2 interconnected by a weightless spring rest on a smooth horizontal plane. The discs are set in motion with initial velocities v1 and v2 whose directions are mutually perpendicular and lie in a horizontal plane. Find the total energy ˜E of this system in the frame of the centre of inertia.
View SolutionA small disc and a thin uniform rod of length l, whose mass is η times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horiozontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of η will the velocity of the disc after the collision be equal to zero? reverse its direction?
View Solution

