Find the current density as a funciton of distance r from the axis of a radially symmetrical parallel stream of electrons if the magentic induction inside the strems varies as B=br2, wheree bandalpha are positive contans.
By Circulation theorem
Bφ2πr=μ0∫r0j(r')×2πr'dr'
or using Bφ=bra inside the streram,
brα+1=μ0∫r0j(r')r'dr'
So by differenctiation,
(α+1)btα=μ0j(r)r
Hence, j(r)=b(α+1)μ0rα−1
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction84videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Find the current density as a funciton of distance r from the axis of a radially symmetrical parallel stream of electrons if the magentic induction inside the strems varies as B=br2, wheree bandalpha are positive contans.
View SolutionUsing the betatron condition, find the radius of a round orbit of an electron if the magnetic induction is known as a function of distance r from the axis of the field. Examine this problem for the specfic case B=B0−αr2, where B0 and a are positive constants.
View Solution
Knowledge Check
- Question 1 - Select One
The current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
ATotal current passing through the cross-section of the wire isI=πJ0a32BTotal current passing through the cross-section of the wire isI=3πJ0a32CThe field at a distance r gt a is B=μ0J0a34rDThe field at a distance r gt a is B=μ0J0a34a - Question 2 - Select One
The magnetic flux denisty B at a distance r from a long stright rod carrying a steady current varies with r as show in the
A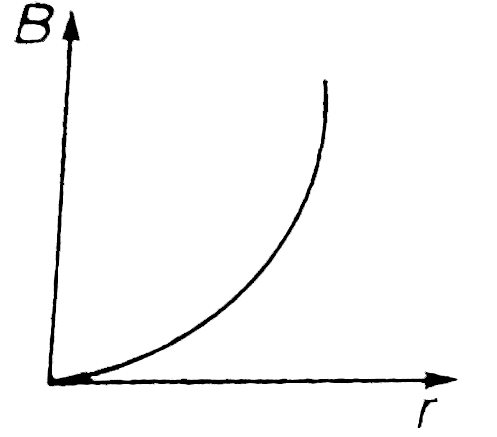 B
B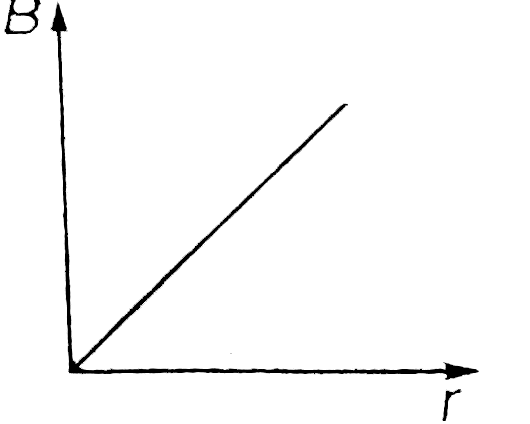 C
C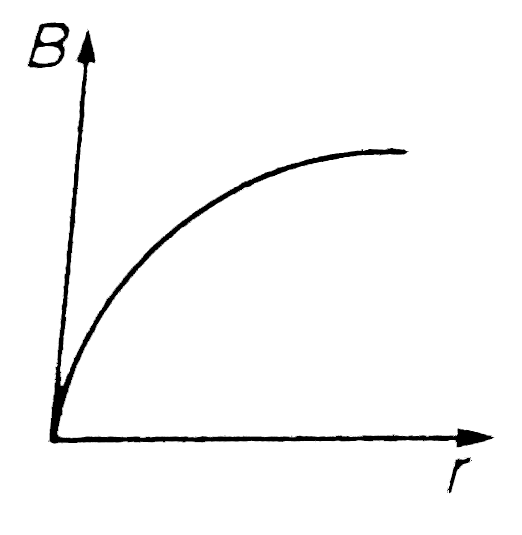 D
D
- Question 3 - Select One
Ampere's law provides us an easy way to calculate the magnetic field due to a symmetrical distribution of current. Its mathemfield expression is ∮→B.dl=μ0Iin.
The quantity on the left hand side is known as line as integral of magnetic field over a closed Ampere's loop.
If the current density in a linear conductor of radius a varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor, find the magnetic field induction at a point distance r from the axis when rlta. Assume relative permeability of the conductor to be unity.Aμ0ka44rBμ0kr32Cμ0kπa42rDμ0ka34
A unifrom current of density f flows inside an infinite plate of thickness 2d parallel to its surface . Find the magentic induction induced by this current as a funcition of the distance x from the median palane of the plate. The magnitude permeability is assumed to be equal to unity both inside and outside the plates.
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View SolutionA hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
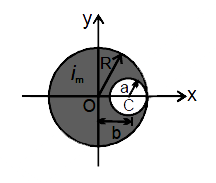
on the y = axis at y = 2R.View SolutionA very long straight conductor has a circular cross- section of radius R and carries a current density J. Inside the conductor there is a cylindrical hole of radius a whose axis is parallel to the axis of the conductor and a distance b from it. Let the z-axis be the axis of the conductor, and let the axis of the hole be at x = b. Find the magnetic field
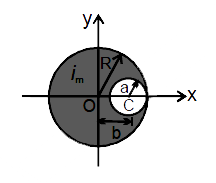
on the x=axis at x = 2RView Solution

