चित्र में, ABC और BDE बड़े दो समबाहु त्रिभुज इस प्रकार है कि D, BC का मध्य-बिन्दु है। यदि AE, BC को F पर प्रतिच्छेद करती है, तो दिखाइए कि
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)
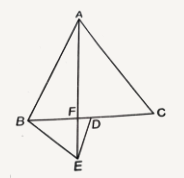
EC और AD को मिलाया।
माना ΔABC की भुजा 'a' है। तब
ar(ΔABC)=a2√34=Δ (माना)

(i) ar(ΔBDE)=(a2)2√34=14×a2√34
=14Δ=14ar(ΔABC) ...(1)
(ii) ∵DE,ΔBEC की माध्यिका है।
∴ar(ΔBDE)=12ar(ΔBEC) (∵ माध्यिका त्रिभुज को दो बराबर क्षेत्रफलो में विभाजित करती है)
अब, ∠(1)=60∘=∠(2) (प्रत्येक समबाहु त्रिभुज का कोण है)
परन्तु ये एकान्तर कोण है।
∴BE∣∣AC
∴ar(ΔBEC)=ar(ΔBAE) (∵ त्रिभुज समान आधार BE और समान समान्तर रेखाओं BE और AC के मध्य है)
∴ समीकरण (2) और (3) से
ar(ΔBDE)=12ar(ΔBAE)
(ii) अब ar(ΔBDE)=12ar(ΔBEC) [(2) से]
⇒14ar(ΔABC)=12ar(ΔBEC) [(1) और (2) से]
⇒ar(ΔABC)=2ar(ΔBEC)
(iv) ∠3=∠4=60∘ प्रत्येक समबाहु त्रिभुज का कोण है)
परन्तु ये एकान्तर कोण है।
∴BA∣∣ED
∴ar(ΔBDE)=ar(ΔAED) (∵ त्रिभुज समान आधार DE और समान समान्तर रेखाओं DE और AB के मध्य है)
⇒ar(ΔBDE)−ar(ΔFED)=ar(ΔAED)−ar(ΔFED)
⇒ar(ΔBEF)=ar(ΔAFD) ...(4)
(v) हम जानते है कि एक समबाहु त्रिभुज में माध्यिका और शीर्षलम्ब समान होते है।
∴AD⊥BC
∴ΔABD में, (पाइथागोरस प्रमेय से)
a2−(a2)2=3a24
∴AD=a√32
EG⊥BD खींचते हे।
∴ΔBED में, EG2=DE2−DG2
=(a2)2−(a4)2=a24−a216=3a216
∴EG=a√34
∴ar(ΔAFD)=12×FD×AD=12×FD×a√32 ...(5)
और ∴ar(ΔEFD)=12×FD×EG=12×FD×a√32 ...(6)
(5) और (6) से
ar(ΔAFD)=2ar(ΔEFD) ...(7)
∴ (4) और (6) से
ar(ΔBEF)=ar(ΔAFD)=2ar(ΔEFD) ...(8)
(vi) ∵ar(ΔBDE)=14ar(ΔABC) [समीकरण (1) से]
⇒ar(ΔBEF)+ar(ΔEFD)=14×2ar(ΔADC)
⇒2ar(ΔFED)+ar(ΔFED)=12[ar(ΔAFC)−ar(ΔAFD)] [समीकरण (8) से]
⇒3ar(ΔFED)=12ar(ΔAFC)−12×2ar(ΔFED) [समीकरण (7) से]
∴4ar(ΔFED)=12ar(ΔAFC)
⇒ar(ΔFED)=18ar(ΔAFC)
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली
27 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.1
1 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
एक समान्तर चतुर्भुज का आधार, संगत शीर्षलम्ब का 3 गुना है। यदि समान्तर चतुर्भुज का क्षेत्रफल 48 वर्ग सेमी है, तो समान्तर चतुर्भुज का आधार और संगत शीर्षफ़ल ज्ञात कीजिए।
View Solutionनिम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित है? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।
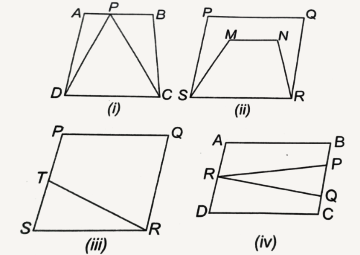
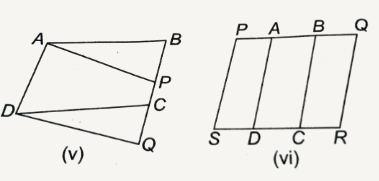
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

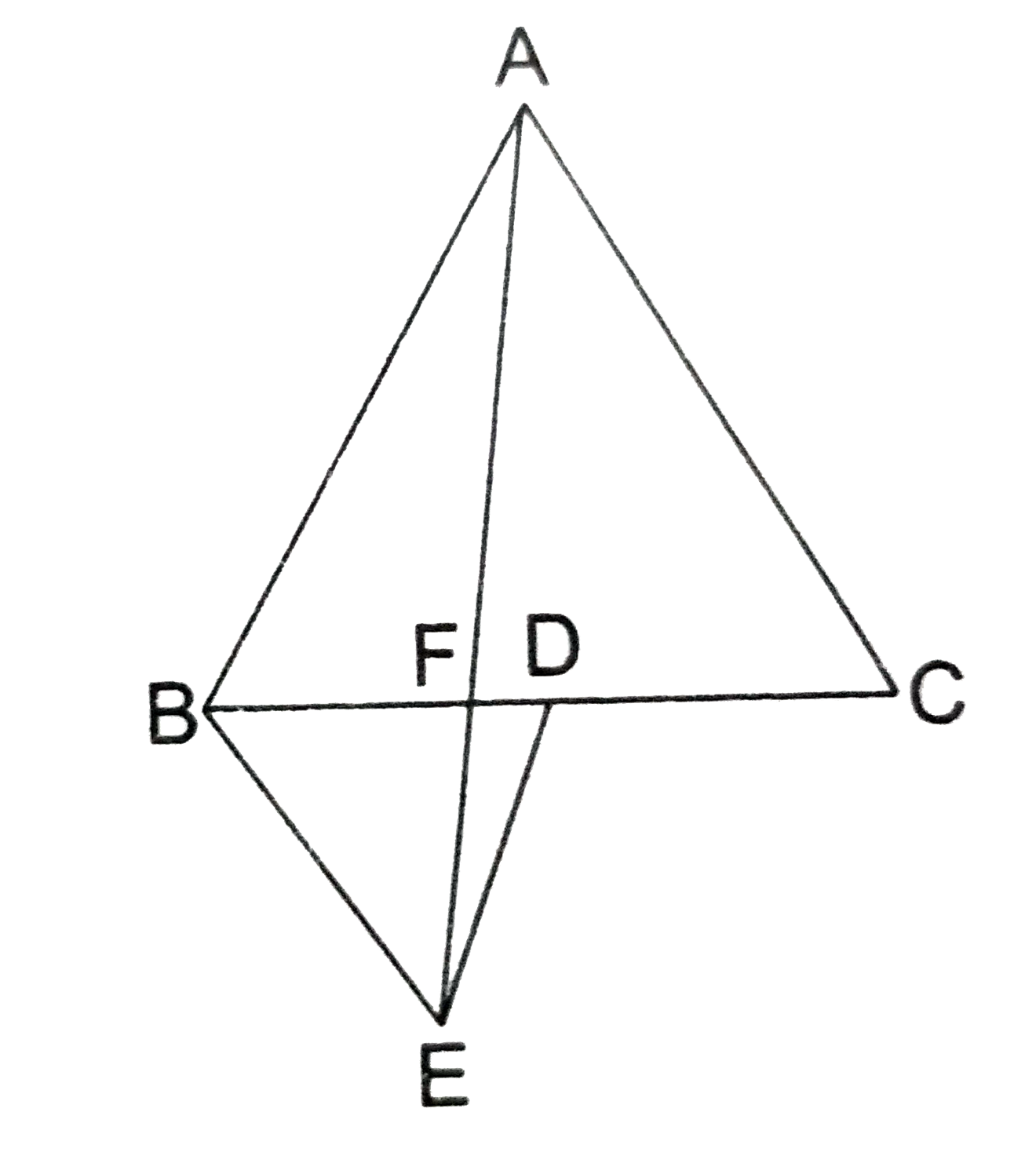
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
View Solutionयदि ΔABC की माध्यिकायें बिंदु G पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि
ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionΔABC में, भुजाओं AB तथा BC के मध्य-बिंदु क्रमशः P तथा Q है और AP का मध्य-बिंदु R है। सिद्ध कीजिए कि
(i)ar(ΔPBQ)=ar(ΔARC) (ii)ar(ΔPRQ)=12ar(ΔARC)
(iii)ar(ΔRQC)=38ar(ΔABC)
View SolutionΔABC में, भुजाओं AB तथा AC पर क्रमशः बिंदु L तथा M इस प्रकार है कि LM ।। BC सिद्ध कीजिए कि
(i) ar(ΔLCM)=ar(ΔLBM)
(ii) ar(ΔLBC)=ar(ΔMBC)
(iii) ar(ΔABM)=ar(ΔACL)
(iv) ar(ΔLOB)=ar(ΔMOC)
View Solutionदिए गए आकृति में ABC और BDF दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य बिंदु है |यदि AE भुजा BC को F पर प्रतिच्छेद करती है तो दर्शाई की
ar(BDF)=14ar(ABC)
(ii) ar(BDE)=12ar(BAE) ltBrgt (iii) ar(ABC)=2ar(BEC)
(iv) ar(BEF)=ar(AFD) ltBrgt (v) ar(BEF)=2ar(FED)
(vi)ar(FED)=18ar(AFC)
View Solutionयदि ΔABC~ΔPQR तथा BC=5QR तो ar(ΔABC):ar(ΔPQR) है
View Solutionसत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View Solution
