For a particle executing simple harmonic motion, the displacement x is given by x= $A cos ω t$ . Identify the graph, which represents the variation of potential energy (U) as a function of time t and displacement x.

A

I, IV

B

I, III

C

II, IV

D

II, III

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

(i) For the particle, $x = A cos ω t$ i.e. it starts from the extreme position.
Its $P . E . = \frac{1}{2} m ω^{2} x^{2} = \frac{1}{2} m ω^{2} (A^{2} {cos}^{2} ω t)$
We will consider its P.E. as a function of time
At time $t = 0, P . E . = \frac{1}{2} m ω^{2} A^{2}$
This is maximum P.E.
$∴$ The correct graph is (1).
(ii) $P . E . = \frac{1}{2} m ω^{2} x^{2}$
We will consider its P.E. as a function of x.
At x=0, P.E. =0 and at $x = \pm A$ , P.E. is maximum .
This is shown in graph (III).
Thus the correct choice is (b) I, III.

|

Updated on:21/07/2023

Class 12 PHYSICS OSCILLATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
For a particle executing S.H.M. the displacement x is given by $x = A cos ω t$ . Identify the graph which represents the variation of potential energy (P.E.) as a function of time
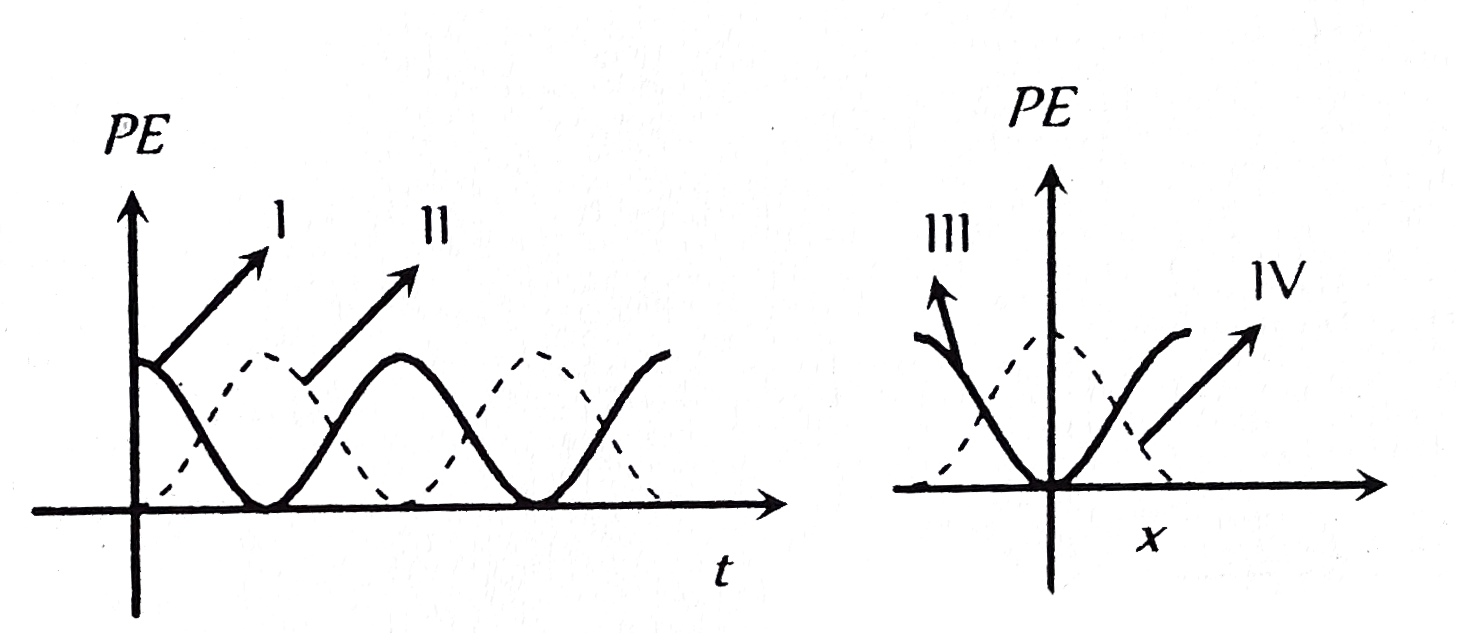AI,III
BII, IV
CII, III
DI,IV
Question 2 - Select One
The total energy of a particle executing simple garmonic motion is $(x -$ displacement)
A $\propto x$
B $\propto x^{2}$
CIndependent of $x$
D $\propto x^{1 / 2}$
Question 3 - Select One
A body executes simple harmonic motion. At a displacement x, its potential energy is $U_{1}$ . At a displacement y, its potential energy is $U_{2}$ . What is the potential energy of the body at a displacement (x + y)?
A $U_{1} + U_{2}$
B ${({\sqrt{U}}_{1} + {\sqrt{U}}_{2})}_{1}^{2}$
C $\sqrt{U_{1}^{2} + U_{2}^{2}}$
D $\sqrt{U_{1} U_{2}}$

MARVEL PUBLICATION-OSCILLATIONS-MCQ

Home
Ask Doubt
Profile